$- q$ तथा $+ q$ आवेश क्रमश: $(0, 0, - a)$ तथा $(0, 0, + a)$ पर स्थित हैं ।
(a) बिंदु $P (0, 0, z)$ तथा बिंदु $Q (x, y, 0)$ पर स्थिर विधुत-विभव ज्ञात करें ।|
(b) मूलबिंदु (origin) से किसी दूरी r पर विभव की निर्भरता (dependence) ज्ञात करें । यदि $\frac{q}{r} < < 1$ .
(c ) x-अक्ष पर बिंदु $(5, 0, 0)$ से दूसरे बिंदु $(- 7, 0, 0)$ तक किसी परीक्षण आवेश को ले जाने में कितना कार्य संपादित होगा ? यदि वह परीक्षण आवेश उन्हीं दो बिंदुओं के बीच x-अक्ष के अनुदिश नहीं, बल्कि किसी अन्य पथ से ले जाएं तो क्या संपादित कार्य का परिमाण बदल जाएगा?

Video Solution

Text Solution

Verified by Experts

चित्र में z-अक्ष पर स्थित -q तथा +q आवेशों से बना निकाय एक विधुत-द्विध्रुव है
जिसका अक्ष धनात्मक z-अक्ष के अनुरेख है । इस द्विध्रुव का आघूर्ण $| \to p | = q .2 a$ .

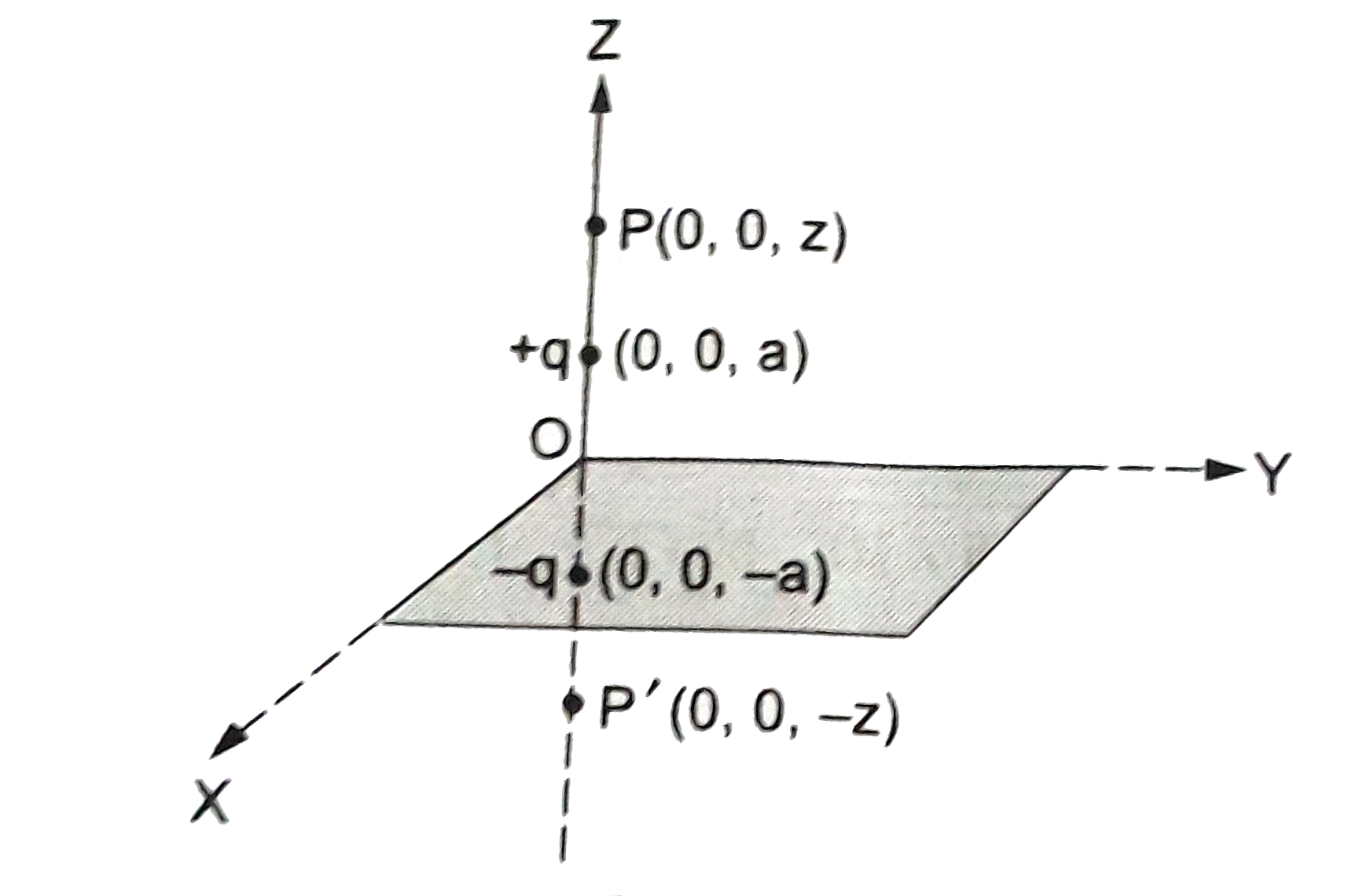
(a)अब बिंदु $P (0, 0, z)$ पर निकाय के कारण विधुत-विभव,
$V = V_{1} + V_{2} = \frac{1}{4 π \in_{0}} [\frac{q}{z - a} + \frac{- q}{z - (- q)}]$
$= \frac{q}{4 π \in_{0}} [\frac{z + a - z + a}{z^{2} - a^{2}}] = \frac{1}{4 π \in_{0}} \frac{q .2 a}{z^{2} - a^{2}}$
$= \frac{1}{4 π \in_{0}} \frac{p}{z^{2} - a^{2}}$
यदि बिंदु P की स्थिति -q आवेश के निकट P' पर हो,तब
$V = \frac{1}{4 π \in_{0}} [\frac{q}{a - (- z)} + \frac{- q}{- a - (- z)}] = \frac{q}{4 π \in_{0}} [\frac{1}{z + a} - \frac{1}{z - a}]$
$= \frac{1}{4 π \in_{0}} \frac{- q .2 a}{z^{2} - a^{2}} = - \frac{1}{4 π \in_{0}} \frac{p}{z^{2} - a^{2}}$
यदि बिंदु Q की स्थिति XY तल में (x,y,0) पर हो, तब आवेश +q से बिंदु Q की दूरी ,
$r_{1} = {[{(x - 0)}^{2} + {(y - 0)}^{2} + {(0 - a)}^{2}]}^{\frac{1}{2}} = \sqrt{x^{2} + y^{2} + a^{2}}$ .
इसी प्रकार, -q से बिंदु Q की दूरी,
$r_{2} = {[{(x - 0)}^{2} + {(y - 0)}^{2} + {(0 + a)}^{2}]}^{\frac{1}{2}} = \sqrt{x^{2} + y^{2} + a^{2}}$ .
स्पष्टत : $r_{1} = r_{2}$ और बिंदु Q पर विधुत-विभव,
$V = V_{1} + V_{2} = \frac{1}{4 π \in_{0}} [\frac{q}{r_{1}} + \frac{- q}{r_{2}}]$

$= \frac{1}{4 π \in_{0}} [\frac{q}{r} - \frac{q}{r}]$ [क्योकि $r_{1} = r_{2} = r$ ]
$= 0$
(b)
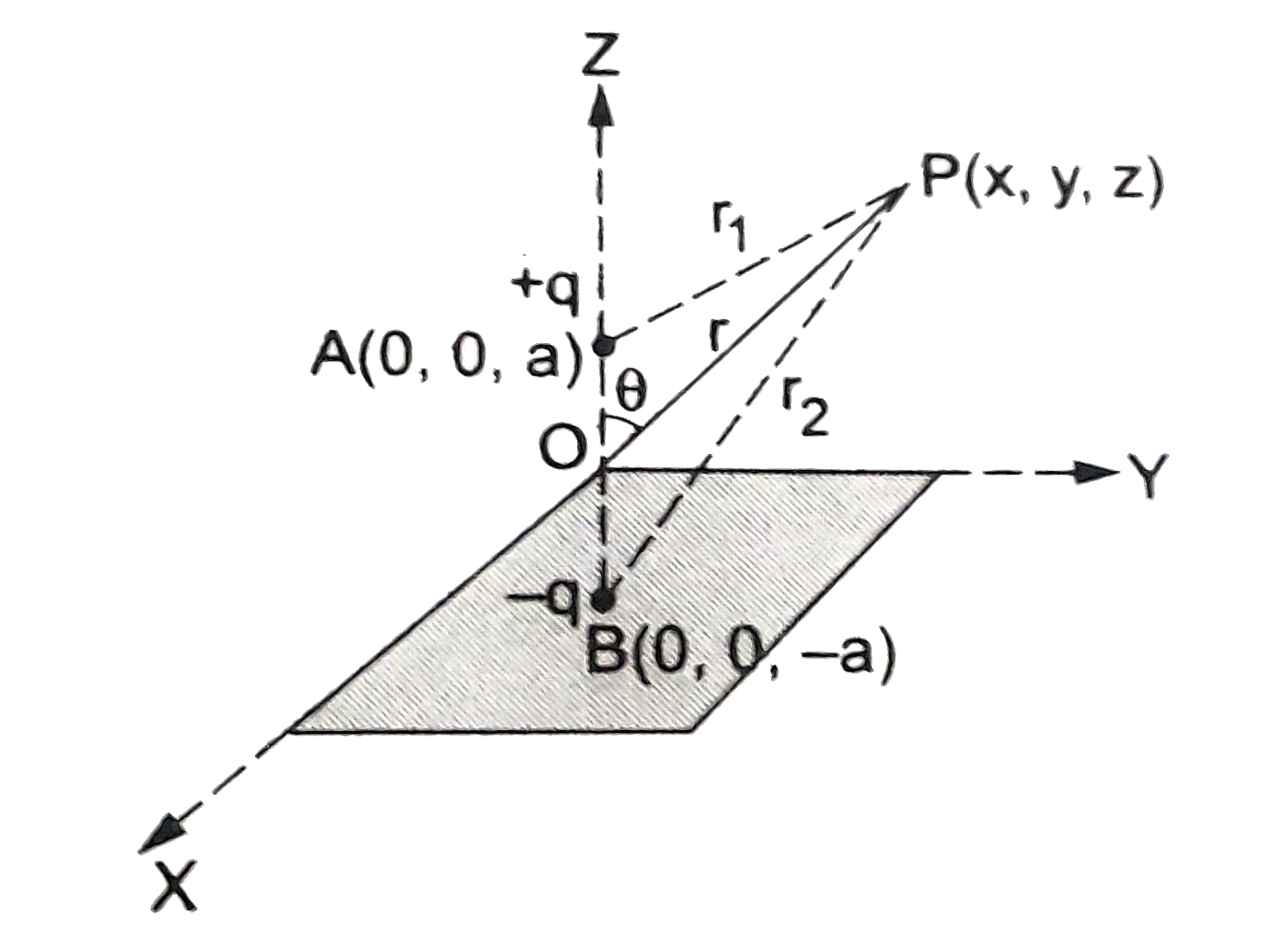मूलबिंदु O से आकाश (space) में किसी स्वेच्छ (arbitrary) बिंदु $P (x, y, z)$ पर विभव:
चित्र में बिंदु A पर स्थित आवेश q से स्वेच्छ बिंदु P की दूरी ,
$r_{1} {[x^{2} + y^{2} + {(z - a)}^{2}]}^{\frac{1}{2}}$
$= {[x^{2} + y^{2} + z^{2} - 2 a z + a^{2}]}^{\frac{1}{2}}$
$= {[r^{2} - 2 a z + a^{2}]}^{\frac{1}{2}}$
$= {[r^{2} - 2 a z]}^{\frac{1}{2}}$ (क्योकि $a^{2} < < r^{2}$ )
$= r {[1 - \frac{2 a z}{r^{2}}]}^{\frac{1}{2}} = r [1 - \frac{1}{2} \frac{2 a z}{r^{2}}]$ (द्विपद प्रमेय से)
$∴ \frac{1}{r_{1}} = \frac{1}{r} {[1 - \frac{a z}{r^{2}}]}^{- 1} = \frac{1}{r} (1 + \frac{a z}{r^{2}})$ .
इसी प्रकार, आवेश -q से बिंदु P की दूरी,
$r_{2} = {[x^{2} + y^{2} + {(z - a)}^{2}]}^{\frac{1}{2}} = {[r^{2} + 2 a z]}^{\frac{1}{2}} = r [1 + \frac{a z}{r^{2}}]$
$∴ \frac{1}{r_{2}} = \frac{1}{r} {(1 + \frac{a z}{r^{2}})}^{- 1} = \frac{1}{r} (1 - \frac{a z}{r^{2}})$ .
अतः बिंदु P पर परिणामी विभव,
$V = V_{1} + V_{2} = \frac{1}{4 π \in_{0}} [\frac{q}{r_{1}} + \frac{- q}{r_{2}}]$
$= \frac{q}{4 π \in_{0}} \frac{1}{r} [(1 + \frac{a z}{r^{2}}) - (1 - \frac{a z}{r^{2}})] = \frac{q}{4 π \in_{0}} . \frac{2 a z}{r^{3}}$
$= \frac{1}{4 π \in_{0}} \frac{(q .2 a)}{r^{2}} \frac{z}{r} = \frac{1}{4 π \in_{0}} \frac{p cos θ}{r^{2}}$ [क्योकि $z = r cos θ$ ]
स्पष्टत: r की तुलना में a का मान उपेक्षणीय रहने पर द्विध्रुव के कारण विभव की r पर निर्भरता $r^{2}$ की व्युत्क्रमानुपाती होती है, अर्थात $V \propto \frac{1}{r^{2}}$ .

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

BHARATI BHAWAN-विद्युत -विभव : विद्युत - द्विध्रुव -उदाहरण

Home
Ask Doubt
Profile