A point charge Q is placed at the origin of the coordinate system. What is the electrostatic energy within an annular spherical region, with centre at origin and inner and outer radius R and 2R respectively.
To find the electrostatic energy within an annular spherical region with a point charge Q placed at the origin, we can follow these steps:
Step 1: Define the Problem
We have a point charge Q at the origin, and we need to calculate the electrostatic energy in the annular region between the inner radius R and the outer radius 2R.
Step 2: Understand the Concept of Capacitance
The capacitance C of a spherical capacitor is given by the formula:
C=4πϵ0r
where r is the radius of the sphere.
Step 3: Calculate the Capacitance for Inner and Outer Spheres
1. For the inner sphere of radius R:
Cinner=4πϵ0R
2. For the outer sphere of radius 2R:
Couter=4πϵ0(2R)=8πϵ0R
Step 4: Calculate the Electrostatic Energy
The electrostatic energy U stored in a capacitor is given by:
U=Q22C
1. For the inner sphere:
Uinner=Q22Cinner=Q22⋅4πϵ0R=Q28πϵ0R
2. For the outer sphere:
Uouter=Q22Couter=Q22⋅8πϵ0R=Q216πϵ0R
Step 5: Calculate the Energy in the Annular Region
The total energy U in the annular region is the difference between the energy in the outer sphere and the energy in the inner sphere:
U=Uouter−Uinner=(Q216πϵ0R)−(Q28πϵ0R)
Step 6: Simplify the Expression
To combine the two terms, we need a common denominator:
U=Q216πϵ0R−2Q216πϵ0R=Q2−2Q216πϵ0R=−Q216πϵ0R
However, since energy cannot be negative in this context, we should state the absolute value:
U=Q216πϵ0R
Final Answer
Thus, the electrostatic energy within the annular spherical region is:
U=Q216πϵ0R
---
We have a point charge Q at the origin, and we need to calculate the electrostatic energy in the annular region between the inner radius R and the outer radius 2R.
The capacitance C of a spherical capacitor is given by the formula:
C=4πϵ0r
where r is the radius of the sphere.
1. For the inner sphere of radius R:
Cinner=4πϵ0R
Couter=4πϵ0(2R)=8πϵ0R
The electrostatic energy U stored in a capacitor is given by:
U=Q22C
Uinner=Q22Cinner=Q22⋅4πϵ0R=Q28πϵ0R
Uouter=Q22Couter=Q22⋅8πϵ0R=Q216πϵ0R
The total energy U in the annular region is the difference between the energy in the outer sphere and the energy in the inner sphere:
U=Uouter−Uinner=(Q216πϵ0R)−(Q28πϵ0R)
To combine the two terms, we need a common denominator:
U=Q216πϵ0R−2Q216πϵ0R=Q2−2Q216πϵ0R=−Q216πϵ0R
U=Q216πϵ0R
Thus, the electrostatic energy within the annular spherical region is:
U=Q216πϵ0R
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-J Aakash Challengers Questions
5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXERCISE
20 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-H Multiple True-False Type Questions
4 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTECHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
16 Videos
Similar Questions
A point charge Q is placed at the origin of the coordinate system. What is the electrostatic energy within an annular spherical region, with centre at origin and inner and outer radius R and 2R respectively.
View SolutionA point charge Q is placed at the origin . Find the electrostatic energy stored outside the sphere of radius R centred at the origen.
View Solution
Knowledge Check
A non-conducting sphere has a total charge Q, uniformly distributed throughout its volume.The centre of the sphere is at origin and its radius is R. Let U1 be the electrostatic potential energy is the region inside the sphere and U2 be the electrostatic potential energy is another imaginary spherical sphell, having inner radius R and outer radius infinity, centred at origin . Select the correct alternative(s)
AU1=Q28πε0RBU2=Q28πε0RCU1+U2=35×Q24πε0RDU1=3Q220πε0RThe electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre
AQ4πε0r for points outside and Q4πε0R for points inside the shellBQ4πε0e for both points inside nad outside the shellCzero for points outside and Q4πε0r for points inside the shellDzero for both points inside and outside the shell
A point charge q is placed at the origin . How does the electric field due to the charge very with distance r from the origin ?
View SolutionWhat is the volume of the material in a spherical shell with inner radius ‘r' and outer radius 'R' ?
View SolutionA point charge +q is placed at the centre of a conducting spherical shell of inner radius a and outer radius b. Find the charge appearing on the inner and outer surface of the shell.
View SolutionA point charge +Q is placed at the centre of an isolated conducting shell of radius R. Find the electrostatic potential energy stored outside the spherical shell if the shell also contains charge +Q distributed uniformly over it.
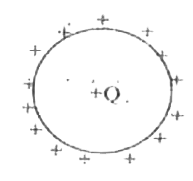
View SolutionA point charge Q is placed at the centre of a circular wire of radius R having charge q. Find the force of electrostatic interaction between point charge and the wire.
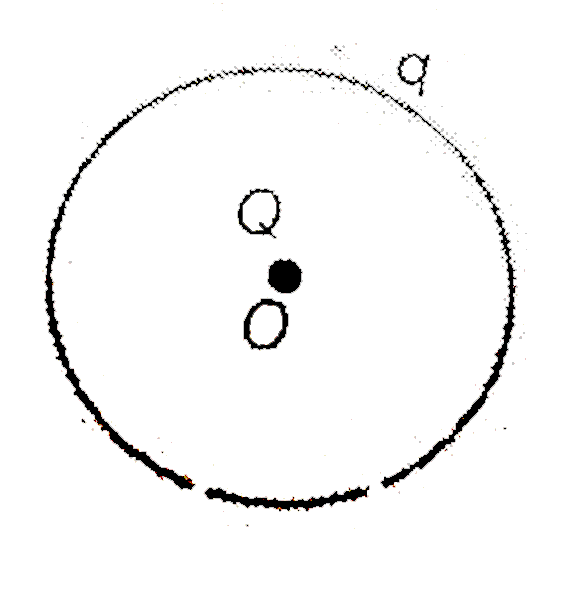
View SolutionBoth question (33) and (34) refer to the system of charges as shown in the figure. A spherical shell with an inner radius 'a' and an outer radius 'b' is made of conducting material. A point charge +Q is placed at the centre of the spherical shell and a total charge -q is placed on the shell.
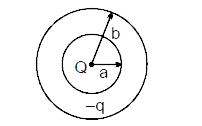
Assume that the electrostatic potential is zero at an infinite distance from the spherical shell. The electrostatic potential at a distance R(a<R<b) from the centre of the shell is
View Solution
