In a certain region of space, variation of potential with distance from origin as we move along x-axis is given by V=8x2+2, where x is the x-coordinate of a point in space. The magnitude of electric field at a point ( -4,0) is
−16V/m
16V/m
−64V/m
64V/m
The correct Answer is:4
To find the magnitude of the electric field at the point (-4, 0), we will use the relationship between electric field (E) and electric potential (V). The electric field is defined as the negative gradient of the electric potential:
E=−dVdx
Given the potential function:
V=8x2+2
we will follow these steps:
Step 1: Differentiate the potential function with respect to x
We need to find the derivative of V with respect to x:
dVdx=ddx(8x2+2)
Step 2: Calculate the derivative
Using the power rule of differentiation:
dVdx=16x
Step 3: Evaluate the derivative at x = -4
Now we will substitute x=−4 into the derivative to find the electric field at that point:
dVdx∣∣∣x=−4=16(−4)=−64
Step 4: Calculate the electric field
Now, we can find the electric field using the relationship we established:
E=−dVdx=−(−64)=64
Conclusion
The magnitude of the electric field at the point (-4, 0) is:
E=64N/C
We need to find the derivative of V with respect to x:
Using the power rule of differentiation:
Now we will substitute x=−4 into the derivative to find the electric field at that point:
Now, we can find the electric field using the relationship we established:
The magnitude of the electric field at the point (-4, 0) is:
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-B (OBJECTIVE TYPE QUESTIONS (ONLY ONE ANSWER) )
1 Video
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-B(OBJECTIVE TYPE QUESTIONS(ONLY ONE ANSWER) )
23 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - TRY YOURSELF
110 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTECHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
16 Videos
Similar Questions
Knowledge Check
In a certain region of space the electric potential V is known to be constant. Is the electric field in this region (a) positive (b) zero ,or (c ) negative ?
AAlso constantBPositiveCNegativeDZeroThe electric potential in a region is given by V=(2x2−3y) volt where x and y are in meters. The electric field intensity at a point (0,3m,5m) is
A−6ˆiN/CB3ˆjN/CC−3ˆjN/CDZeroWe know that electric field (E ) at any point in space can be calculated using the relation
→E=−δVδxˆi−δVδyˆj−δVδzˆk

if we know the variation of potential (V) at that point. Now let the electric potential in volt along the x-axis vary as V=2x2, where x is in meter. Its variation is as shown in figure
Draw the variation of electric field (E ) along the x-axis.A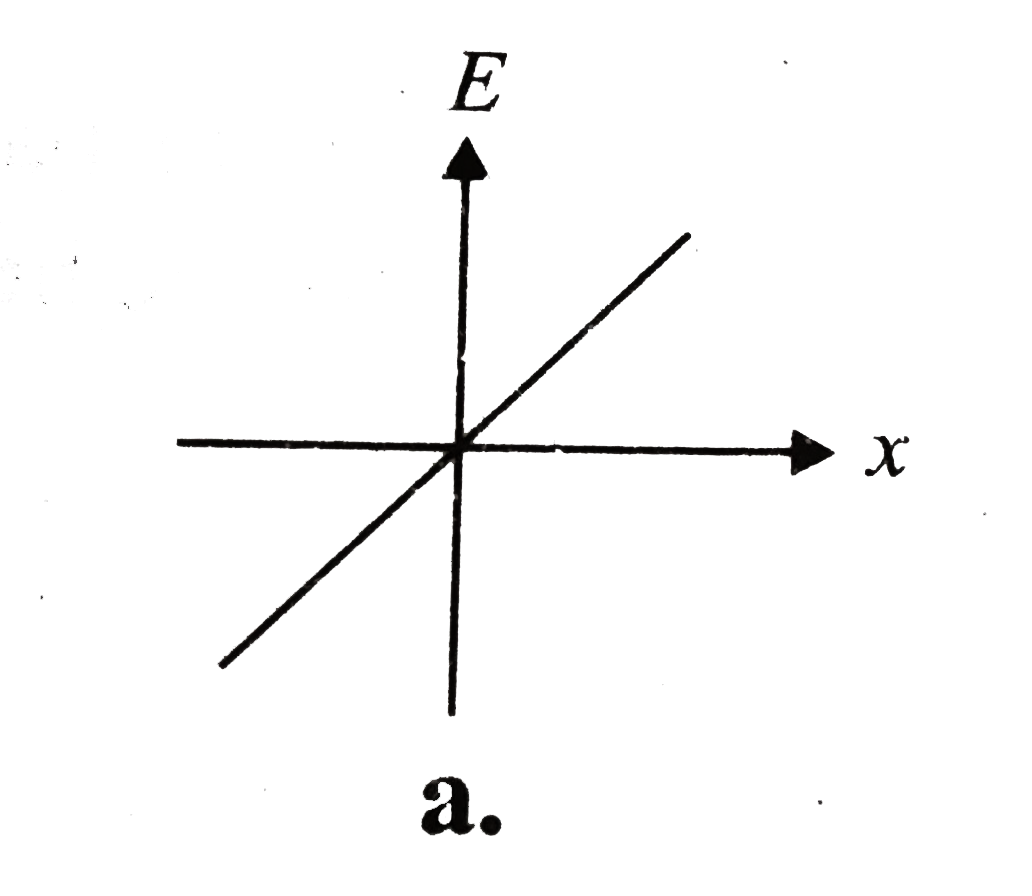 B
B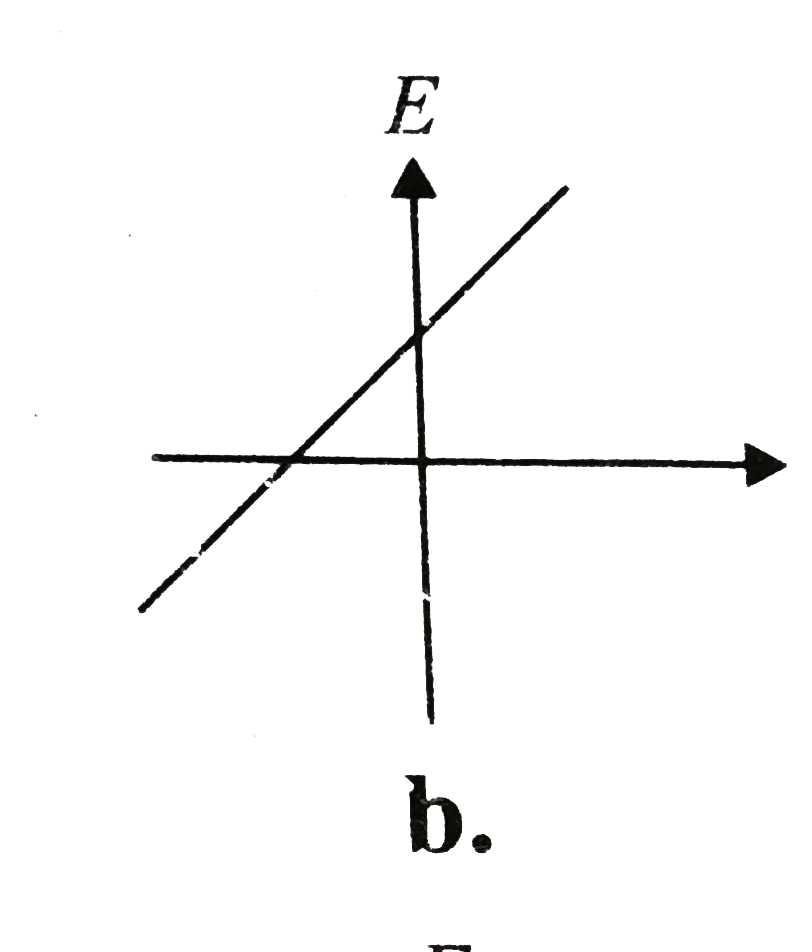 C
C D
D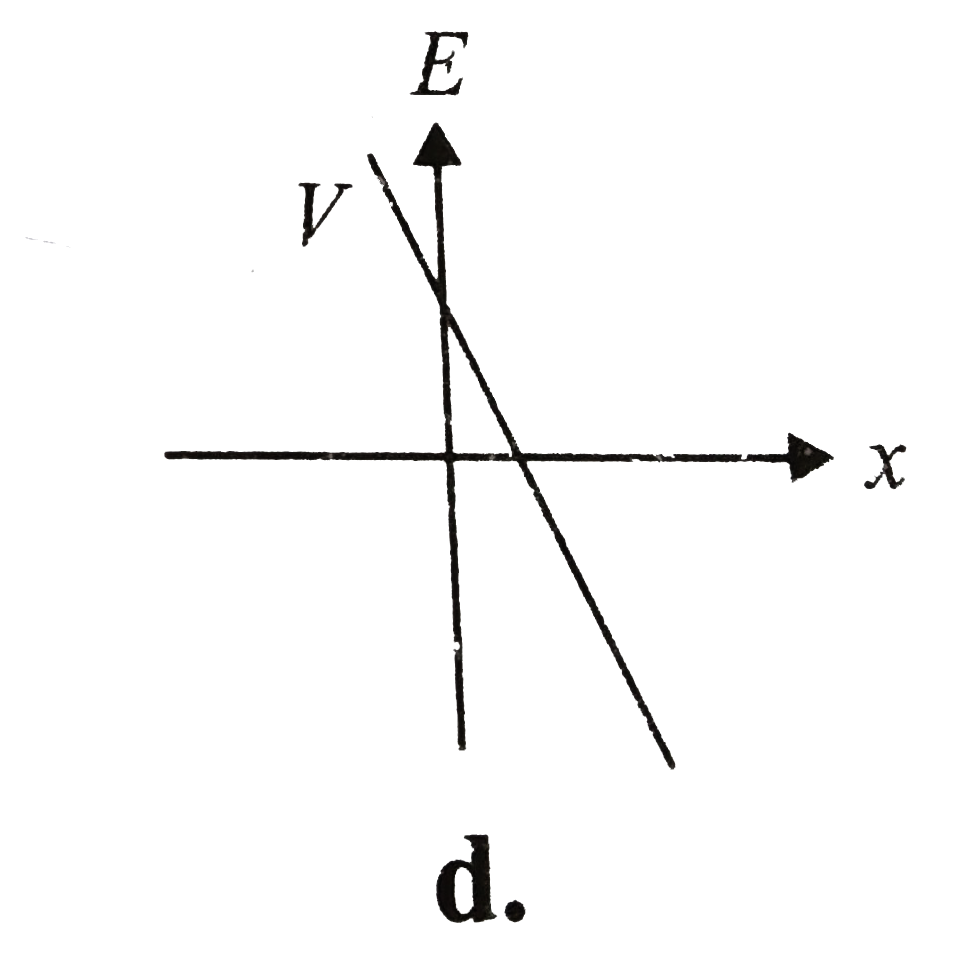
Electric potential at any point V=-4x+3y+5z then magnitude of electric field in the space will be
View SolutionThe potential at any point is given by V=x(y2−4x2). Calculate the cartesian components of the electric field at the point.
View SolutionIf the potential function is given by V=4x+3y then the magnitude of electric field intensity at the point (2 1) will be ......?
View SolutionIf the potentail in the region of space around the point (−1m,2m,3m) is given by V=(10x2+5y2−3z2), calculate the three components of electric field at this point.
View SolutionThe variation of electric potential with distance from a fixed point is shown in figure. What is the value of electric field at x=2m -

View Solution
