Using the concept of energy density , show that the total energy stored by a shell of radius R and charge Q is Q28πε0R
The electric field field at a distance r from centre is
E=Q4πε0r2
The energy stored in a shell of radius r and thickness dr
dU=12ε0E2×4πr2dr
∴dU=12ε0(Q4πε0r2)2×4pr2dr [∵E=Q4πε0r2]
or, dU=Q28πε0drr2
⇒ Total energy stored U=Q28πε0∫∞Rdrr2
⇒U=Q28πε0[−1r]∞n=Q28πε0R

Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:AAKASH INSTITUTEChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:TRY YOURSELF
Explore 110 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:AAKASH INSTITUTEChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:ASSIGNMENT (SECTION-A) Objective Type Questions (Only one answer)
Explore 47 Videos
- ELECTROMAGNETIC WAVESBook:AAKASH INSTITUTEChapter:ELECTROMAGNETIC WAVESExercise:ASSIGNMENT SECTION - D Assertion-Reason Type Questions
Explore 25 Videos
- GRAVITATION Book:AAKASH INSTITUTEChapter:GRAVITATION Exercise:ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
Explore 16 Videos
Similar Questions
Knowledge Check
A spherical conductor having charge q and radius r is placed at the centre of a spherical shell of radius R and having charge Q (R > r). The potential difference between the two is
Aproportional to QBProportional to qCDependent on both Q and qDindependent of both Q and q
A point charge Q is placed at the origin . Find the electrostatic energy stored outside the sphere of radius R centred at the origen.
View SolutionObtain a relation for total energy of the electron in terms of orbital radius. Show that total energy is negative of K.E. and half of potential energy E=−e28πɛ0r
View SolutionA metal sphere of radius R is charged to a pontital V . (a ) Find the electtrostatic energy stored in the electric field within a concentric sphere of radius 2 R . (b )Show that the electrostatic field energy stored outside the sphere of radius 2R equals that stored within it .
View SolutionA particle having charge + q is fixed at a point O and a second particle of mass m and having charge −q0 moves with constant speed in a circle of radius r about the charge +q. the energy required to be supplied to the moving charge to increase radius of the path to 2r is qq0nπε0r. Find the value of n.
View SolutionThere are two spheres of radii R and 2R having charges Q and Q2 respectively. These two spheres are connected with a cell of emf V volts as shown in figure. When switch is closed, the final charge on sphere of radius 2R is Q+8πε0RVn . Then find the value of n.
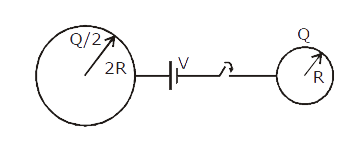
View SolutionCalculate the self potential energy of charge q distributed over the surface of a hollow sphere of radius R. What happens to this self energy when R=0, or when the charge is an ideal point charge?
View SolutionIf Q charge is given to a sphere of radius R, the energy of the system is
View Solution

