Two metallic spheres of radii a and b are placed faraway from each other and are connected for a thin conducting wire. A charge Q is given to one of the spheres . Calculate the charge on each sphere at electrostatic equilibrium.
To solve the problem of finding the charge on each metallic sphere at electrostatic equilibrium when they are connected by a thin conducting wire, we can follow these steps:
1. Understanding the System:
We have two metallic spheres with radii a and b that are far apart and connected by a thin conducting wire. Initially, one of the spheres is given a charge Q.
2. Concept of Electrostatic Equilibrium:
When the spheres are connected by a wire, charge will redistribute between them until they reach the same electric potential. At electrostatic equilibrium, the potential V on both spheres must be equal.
3. Electric Potential of a Sphere:
The electric potential V of a charged sphere is given by:
V=kQ′R
where Q′ is the charge on the sphere and R is its radius. Here, k is Coulomb's constant.
4. Setting Up the Equation:
Let Qa be the charge on sphere A (radius a) and Qb be the charge on sphere B (radius b). Since the total charge is conserved, we have:
Qa+Qb=Q
The potentials of the two spheres must be equal:
kQaa=kQbb
5. Eliminating k:
Since k is a constant, we can eliminate it from the equation:
Qaa=Qbb
6. Expressing Qb in terms of Qa:
From the above equation, we can express Qb as:
Qb=baQa
7. Substituting into the Charge Conservation Equation:
Substitute Qb into the charge conservation equation:
Qa+baQa=Q
Qa(1+ba)=Q
8. Solving for Qa:
Rearranging gives:
Qa=Q1+ba=Qaa+b
9. Finding Qb:
Now, substitute Qa back to find Qb:
Qb=Q−Qa=Q−Qaa+b=Q(a+b)−Qaa+b=Qba+b
Final Charges:
- Charge on sphere A:
Qa=Qaa+b
- Charge on sphere B:
Qb=Qba+b
We have two metallic spheres with radii a and b that are far apart and connected by a thin conducting wire. Initially, one of the spheres is given a charge Q.
When the spheres are connected by a wire, charge will redistribute between them until they reach the same electric potential. At electrostatic equilibrium, the potential V on both spheres must be equal.
The electric potential V of a charged sphere is given by:
V=kQ′R
where Q′ is the charge on the sphere and R is its radius. Here, k is Coulomb's constant.
Let Qa be the charge on sphere A (radius a) and Qb be the charge on sphere B (radius b). Since the total charge is conserved, we have:
Qa+Qb=Q
kQaa=kQbb
Since k is a constant, we can eliminate it from the equation:
Qaa=Qbb
From the above equation, we can express Qb as:
Qb=baQa
Substitute Qb into the charge conservation equation:
Qa+baQa=Q
Qa(1+ba)=Q
Rearranging gives:
Qa=Q1+ba=Qaa+b
Now, substitute Qa back to find Qb:
Qb=Q−Qa=Q−Qaa+b=Q(a+b)−Qaa+b=Qba+b
- Charge on sphere A:
Qa=Qaa+b
- Charge on sphere B:
Qb=Qba+b
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - TRY YOURSELF
110 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT (SECTION-A) Objective Type Questions (Only one answer)
47 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTECHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
16 Videos
Similar Questions
Two small metal spheres A and B, each of radius r and supported on insulating stands, located at a distance a(a>>r) from each other are connected by a thin conducting wire. A point charge q is brought near the spheres at distance l(l>>r) on the line joining the centers of the spheres. What are the moduli of charge induced on the spheres ?
 .
.
View SolutionTwo equally charged spheres A and B with radii rAandrB(rA>rB) are connected by a conducting wire. Will the charge density on both the spheres become equal after connection?
View Solution
Knowledge Check
Two metal spheres of same radius R are placed at a very large distance from each other, and they are connected by a coil of inductance L, as it is shown in the figure. One of the spheres is loaded with electric charge. At what time, after closing the switch S. does the charge on this sphere decreases to half ?
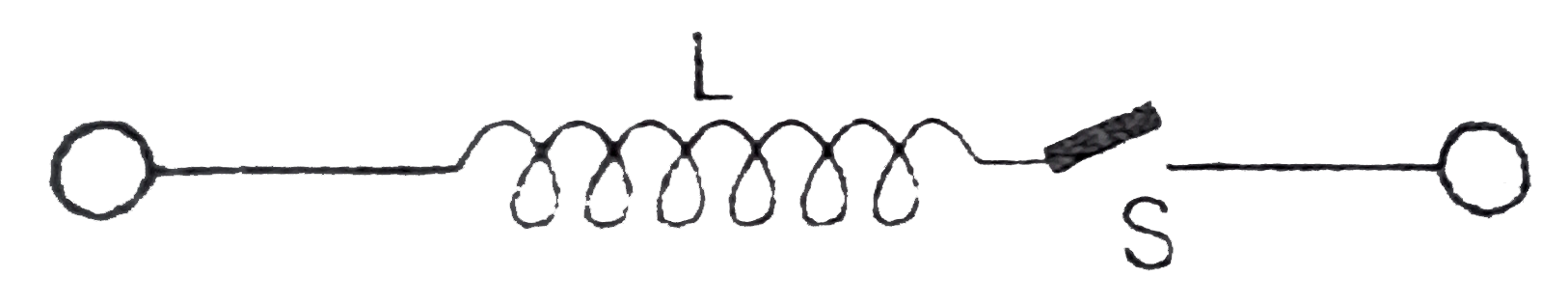 Aπ2√4πε0LRBπ4√4πε0LRCπ2√2πε0LRDπ4√2πε0LR
Aπ2√4πε0LRBπ4√4πε0LRCπ2√2πε0LRDπ4√2πε0LRConsider a neutral conducting sphere. A positive point charge is placed outside the sphere. The net charge on the sphere is then
Anegative and distributed uniformly over the surface of the sphereBnegative and appears only at the point on the sphere closest to the point chargeCnegative and distributed non-uniformly over the entire surface of the sphereDzeroTwo metallic spheres of radius 1 cm and 2 cm are given charge 10−2and5×10−2 C respectively. If they are connected by a conducting wire, the final charge on the smaller sphere is
A3×10−2 CB2×10−2 CC1×10−2CD6×10−2 C
Two isolated metallic solid spheres of radii R and 2R are charged such that both have the same charge Q. The spheres are located far away from each other and connected by a thin conducting wire. Find the heat dissipated in the wire.
View SolutionTwo metallic spheres of radii 1cm and 2cm are given charges 10−2C and 5×10−2C respectively. If they are connected by a conducting wire, the final charge on the smaller sphere is
View SolutionTwo metallic sphere of radii 1cm and 3cm are given charges of 4×10−2C and respectively. If these are connected by a counducting wire, the final charge on the bigger sphere is
View SolutionConsider a neutral conducting sphere. A positive point charge is placed outside the sphere. The net charge on the sphere is then
View SolutionTwo conducting spheres of radii 5cm and 10cm are given a charge of 15μF each. After the two spheres are joined by a conducting wire, the charge on the smaller sphere is
View Solution
