In Gauss's law ε0∮→E.¯¯¯¯ds=Qenclosed, is →E only due to charges enclosed ?
No, this →E field canbe due to all the charges inside as well as outside.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTECHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - TRY YOURSELF
33 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTECHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - ASSIGNMENT(SECTION-A) Objective Type Question
47 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - AAKASH INSTITUTECHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION -D) Assertion-Reason type Question)
15 Videos
Similar Questions
Gauss's law is true only if force due to a charge varies as
View SolutionThe suface integral of electrostatic field →E produced by any sources over any closed surface S enclosing a volume V in vacumm, i.e., total electric flux over the closed S in vacumm is 1/∈0 times the total charge (Q) contained inside S, i.e, ϕE=∮→E.→ds=Q∈0
The charge inside S may be point charges or even continous charge distributions.
There is no contribution to total electric flux from the charges outside S. Further, the location at Q inside S does not affect the value of surface integral.
Read the above passage and answer the following questions :
(i) what are the SI unit and dimensions of electric flux ?
(ii) A closed surface in vacumm encloses charge −q,+3qand+5q. Another charge +4q lies outside the surface. What is total electric flux over the surface ?
(iii) A point charge q lies inside a spherical of radius r. How will the electric flux be affected if radius of the sphere is doubled ?
(iv) What values of life do you earn from the theorem ?
View Solution
Knowledge Check
Statement - 1 : If a concentric spheerical Gaussian surface is drawn inside thin spheical shell charge, electric field (E) at each point of surface must be zero.
Statement - 2 : In accordance with Gauss's law
ϕE=∮→E.d→A=Qnet enclosedε0
Qnet enclosed=0 implies ϕE=0AStatement - 1 is true, Statement - 2 is true and statement -2 is correct explanation for statement - 1.BStatement - 1 is true, Statement - 2 is ture and statement - 2 is NOT correct explanation for statement - 1.CStatement - 1 is true, statement - 2 is false.DStatement - 1 is false, statement - 2 is true.Gauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when q(encl) is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
A Gaussian surface encloses two of the four positively charged particles. The particles that contribute to the electric field at a point P on the surface are
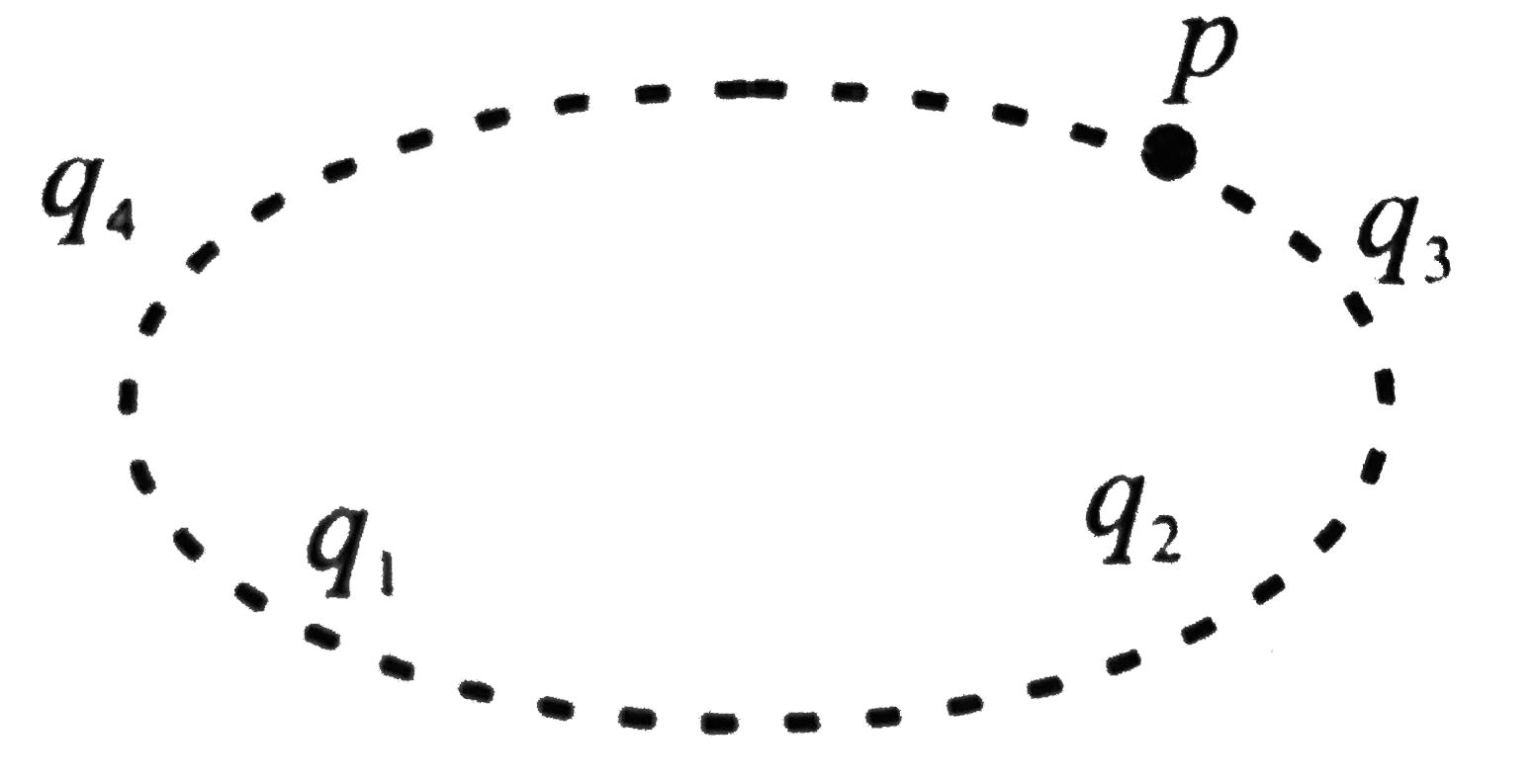 Aq1 and q2Bq2 and q3Cq4 and q3Dq1,q2,q3 and q4
Aq1 and q2Bq2 and q3Cq4 and q3Dq1,q2,q3 and q4Gauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when q(encl) is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
If the charge q3 and q4 are displaced (always remaining outside the Gaussian surface), then consider the following two statements :
A: Electric field at each point on the Gaussian surface will remain same .
B: The value of ∮→E.d→A for the Gaussian surface will remain same.ABoth A and B are true .BBoth A and B are false.CA is true , but b is false.DB is true , but A is false.
Gauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when q(encl) is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
The net flux of the electric field through the surface due to q3 and q4 is
View SolutionGauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when q(encl) is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
The net flux of the electric field through the surface is
View Solutionfive charge q1,q2,q3,q4and q5 are fixed at their positions as shown in figure .s is Gaussian surface .The Gauss's law is given by ∮→E.→ds=qε0
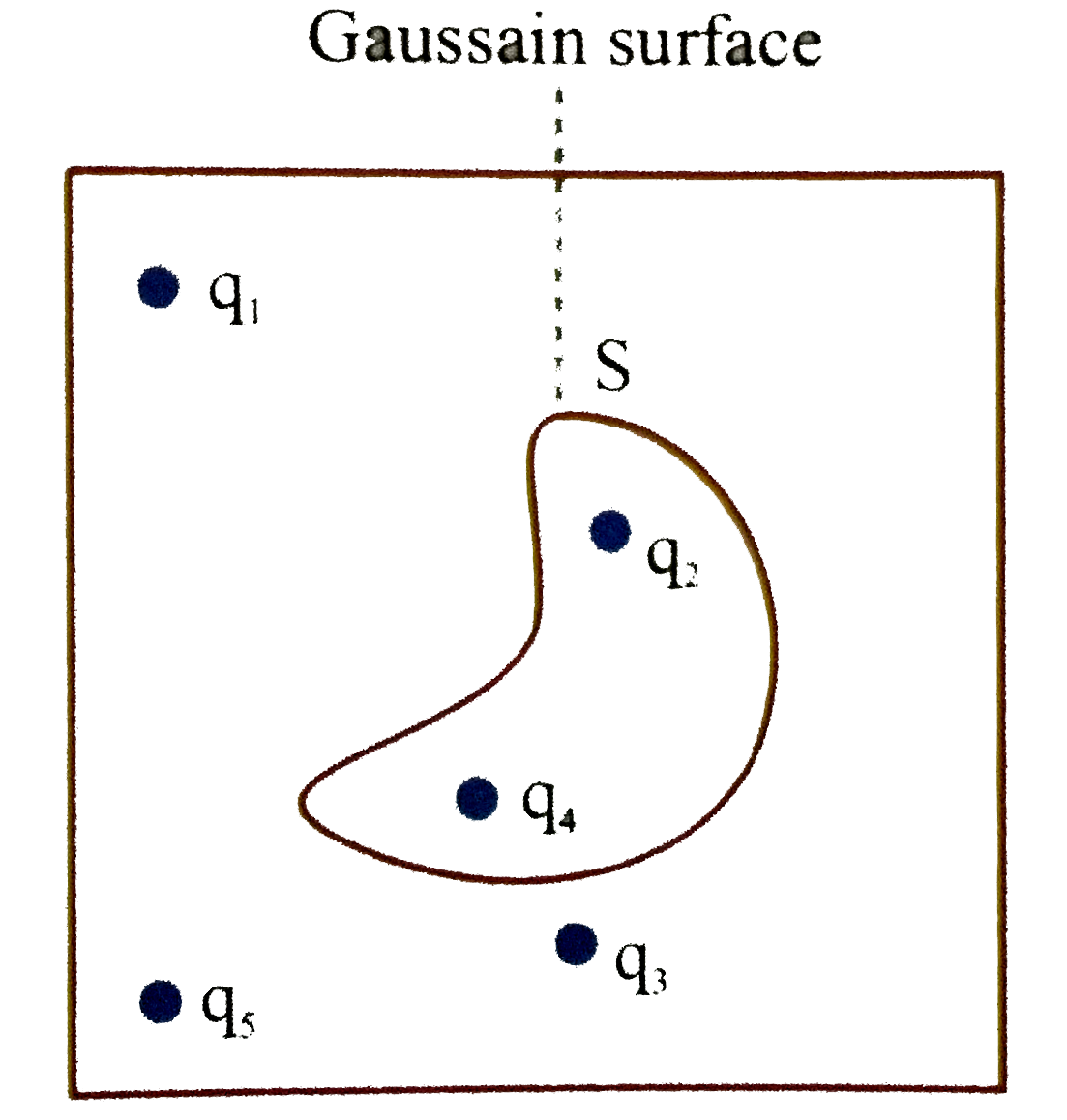
Which of the following statement is correct?
View SolutionAnswer questions on the basis of your understanding of the following paragraph and the related studied concept.
Electric flux, in general , through any surface is defined as per relation:
ϕE=∫→E.→ds , where integration has to be performed over the entire surface through which flux is required. The surface under consideration may be a closed one or an open surface. When flux through a closed surface is required we use a small circular sign on the integration symbol. Thus flux over a closed surface ∮E=∮→E.→ds. it is customary to take the outward normal as positive in this case.
A German physicist Gauss established a fundamental law to find electric flux over a closed surface. As per Gauss' law , the flux of the net electric field through a closed surface equals the net charge enclosed by the surface divided by ∈0.Mathematically ∮→E.→ds=1∈0[qen] , where qcn is the net charge enclosed within the surface. It is possible to derive Gauss' law from Coulomb's laws. Gauss' law can be applied to obtain electric field at a point due to continuous charge distribution for a number of symmetric charge configurations.
A charge q is enclosed by a Gaussian spherical surface of raidus R. If the radius is doubled then the electric flux will.
View SolutionAnswer questions on the basis of your understanding of the following paragraph and the related studied concept.
Electric flux, in general , through any surface is defined as per relation:
ϕE=∫→E.→ds , where integration has to be performed over the entire surface through which flux is required. The surface under consideration may be a closed one or an open surface. When flux through a closed surface is required we use a small circular sign on the integration symbol. Thus flux over a closed surface ∮E=∮→E.→ds. it is customary to take the outward normal as positive in this case.
A German physicist Gauss established a fundamental law to find electric flux over a closed surface. As per Gauss' law , the flux of the net electric field through a closed surface equals the net charge enclosed by the surface divided by ∈0.Mathematically ∮→E.→ds=1∈0[qen] , where qcn is the net charge enclosed within the surface. It is possible to derive Gauss' law from Coulomb's laws. Gauss' law can be applied to obtain electric field at a point due to continuous charge distribution for a number of symmetric charge configurations.
What is the electrical flux through a cube of side 'a' if a point charge 'q' is placed at one of its vertices?
View Solution
