A uniform tube closed at one end, contains a pallet of mercury 4 cm long. When the tube is kept vertically with closed end upwards, the length of air column between closed end and mercury pallet is 10 cm. the tube is inverted so that open end becomes upwards. find the length of trapped air column (in cm) trapped. take atmospheric pressure 76 cm of Hg.
The correct Answer is:9
To solve the problem step by step, we will analyze the situation before and after the tube is inverted.
Step 1: Understand the initial conditions
- The tube is closed at one end and contains a mercury pellet that is 4 cm long.
- When the tube is vertical with the closed end upwards, the length of the air column above the mercury pellet is 10 cm.
- The atmospheric pressure is given as 76 cm of Hg.
Step 2: Calculate the pressure at the closed end when the tube is upright
Using the information provided:
- The total pressure at the closed end (P1) plus the height of the mercury column (4 cm) equals the atmospheric pressure (76 cm):
P1+4 cm=76 cm
P1=76 cm−4 cm=72 cm
Step 3: Analyze the situation after inverting the tube
When the tube is inverted:
- The closed end is now at the bottom, and the open end is at the top.
- The mercury pellet remains 4 cm long, but now it is at the bottom of the tube.
Step 4: Calculate the pressure at the open end when inverted
The pressure at the open end (P2) now includes the atmospheric pressure and the height of the mercury column:
P2=Patm+height of mercury column
Here, the height of the mercury column is still 4 cm:
P2=76 cm+4 cm=80 cm
Step 5: Use the ideal gas law to relate the two states
According to the ideal gas law, the product of pressure and volume remains constant for a given amount of gas:
P1V1=P2V2
Where:
- V1 is the volume of the air column when the tube is upright.
- V2 is the volume of the air column when the tube is inverted.
Step 6: Calculate the volume of the air column
The volume of the air column can be expressed as:
V1=A⋅h1=A⋅10 cm
V2=A⋅h2
Where h1=10 cm and h2 is the unknown length of the air column when inverted.
Step 7: Substitute into the ideal gas equation
Substituting the volumes into the equation:
P1(A⋅10)=P2(A⋅h2)
Canceling the area A from both sides:
P1⋅10=P2⋅h2
Substituting the values of P1 and P2:
72⋅10=80⋅h2
720=80h2
h2=72080=9 cm
Final Answer
The length of the trapped air column when the tube is inverted is 9 cm.
---
- The tube is closed at one end and contains a mercury pellet that is 4 cm long.
- When the tube is vertical with the closed end upwards, the length of the air column above the mercury pellet is 10 cm.
- The atmospheric pressure is given as 76 cm of Hg.
Using the information provided:
- The total pressure at the closed end (P1) plus the height of the mercury column (4 cm) equals the atmospheric pressure (76 cm):
P1+4 cm=76 cm
P1=76 cm−4 cm=72 cm
When the tube is inverted:
- The closed end is now at the bottom, and the open end is at the top.
- The mercury pellet remains 4 cm long, but now it is at the bottom of the tube.
The pressure at the open end (P2) now includes the atmospheric pressure and the height of the mercury column:
P2=Patm+height of mercury column
Here, the height of the mercury column is still 4 cm:
P2=76 cm+4 cm=80 cm
According to the ideal gas law, the product of pressure and volume remains constant for a given amount of gas:
P1V1=P2V2
Where:
- V1 is the volume of the air column when the tube is upright.
- V2 is the volume of the air column when the tube is inverted.
The volume of the air column can be expressed as:
V1=A⋅h1=A⋅10 cm
V2=A⋅h2
Where h1=10 cm and h2 is the unknown length of the air column when inverted.
Substituting the volumes into the equation:
P1(A⋅10)=P2(A⋅h2)
Canceling the area A from both sides:
P1⋅10=P2⋅h2
Substituting the values of P1 and P2:
72⋅10=80⋅h2
720=80h2
h2=72080=9 cm
The length of the trapped air column when the tube is inverted is 9 cm.
Topper's Solved these Questions
- KINETIC THEORYBook:AAKASH INSTITUTEChapter:KINETIC THEORYExercise:Assignment (Section-H) (Multiple True-false Type questions)
Explore 3 Videos
- KINETIC THEORYBook:AAKASH INSTITUTEChapter:KINETIC THEORYExercise:Assignment (Section-I) (Subjective Type Questions)
Explore 5 Videos
- KINETIC THEORYBook:AAKASH INSTITUTEChapter:KINETIC THEORYExercise:Assignment (Section-F) (Matrix-match type questions)
Explore 1 Video
- GRAVITATION Book:AAKASH INSTITUTEChapter:GRAVITATION Exercise:ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
Explore 16 Videos
- LAWS OF MOTIONBook:AAKASH INSTITUTEChapter:LAWS OF MOTIONExercise:Assignment (SECTION-D) (Assertion-Reason Type Questions)
Explore 15 Videos
Similar Questions
In given figure, A uniform cylindrical tube closed at one end, contains a pallet of mercury 5cm long. When the tube is kept verticaly with the closed end downward, the length of the air column trapped is 30cm. Now the tube is inverted so that the closed end goes up find the new length of the air column trapped. atmospheric pressure =75cm of mercury. (Assume temperature remains constant in this process)

View Solution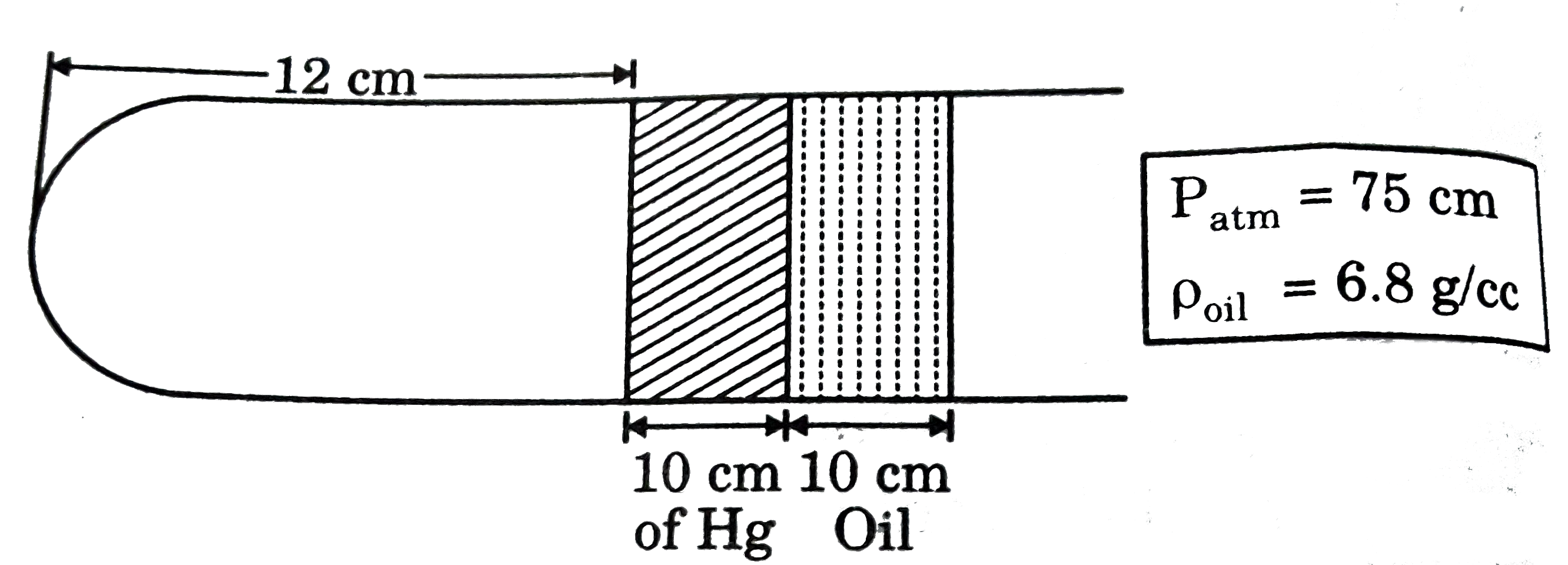
If above tube is held vertical with open end upward then find the length of air column (in cm).
View Solution
Knowledge Check
Some mercury is poured into a capillary tube of uniform bore and one end closed. When the tube is held horizontally, mercury column has a length of 4 cm and air enclosed in the closed end has a length of 10 cm. If the tube is now held vertically, with open end upwards, the length of the air column will be (take atmospheric pressure at the place of experiment to be 760 mm)
A10.5 cmB8.5 cmC9.0 cmD9.5 cmThe length of an air column trapped in a capillary tube by means of a mercury pellet is 5 cm at 30∘C. If the tube is heated uniformly to 80∘C, the new length of air column is :
 A5.83cmB6.83cmC58.3cmD4.87cm
A5.83cmB6.83cmC58.3cmD4.87cmA quill tube contains a mercury column of length 19cm. The length of air column is 24cm when it is held veritcally. On inverting it with its open end downwards the length of air column will be
(atmospheric pressure =76cm of Hg)A20cmB30cmC40cmD35cm
A uniform tube closed at aone end, contains a pellet of mercury 10cm long. When the tube is lept vertically with the closed-end upward, the length of the air column trapped is 20cm. Find the length of the air column trapped when the tube is inverted so that the closed-end goes down. Atmospheric pressure=75cm of mercury.
View Solution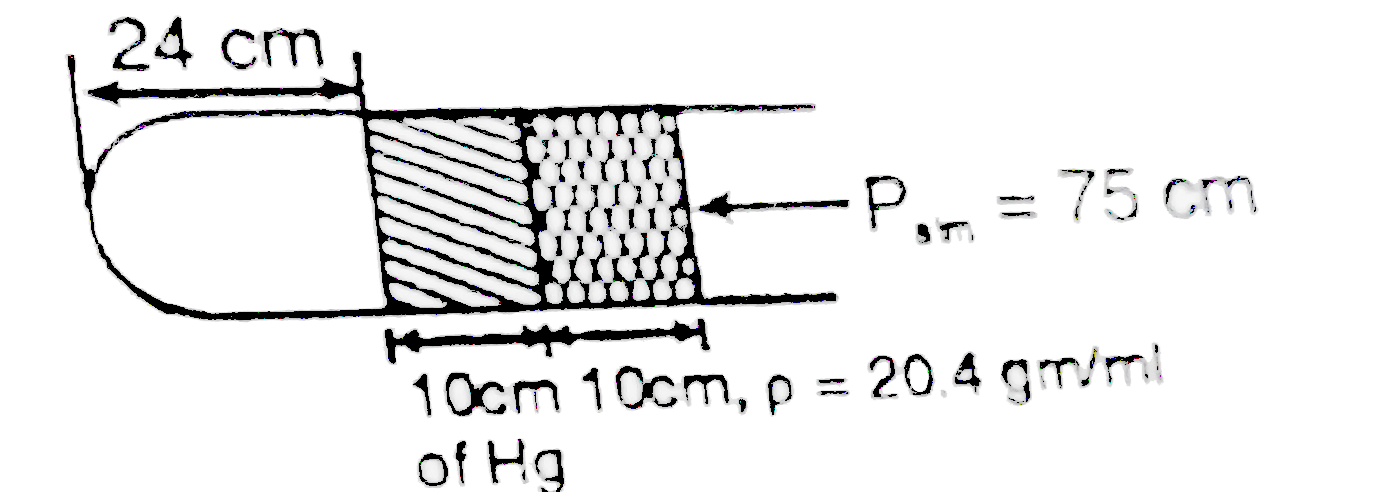
If above tube is placed vertically with the open and upward then find the length of the air column.
View SolutionA barometer tube is inclined at an angle of 30∘ with horizontal direction. Calculate length of mercury column in tube if atmospheric pressure is 76 cm of mercury.
View SolutionAn air column closed in a tube sealed at one end by a Hg column having height h. When the tube is placed with open end down, the height of the air column Iis l1. If the tube is turned so that its open end is at the top, the height of the air column is l2. What is the atmospheric pressure (P0).
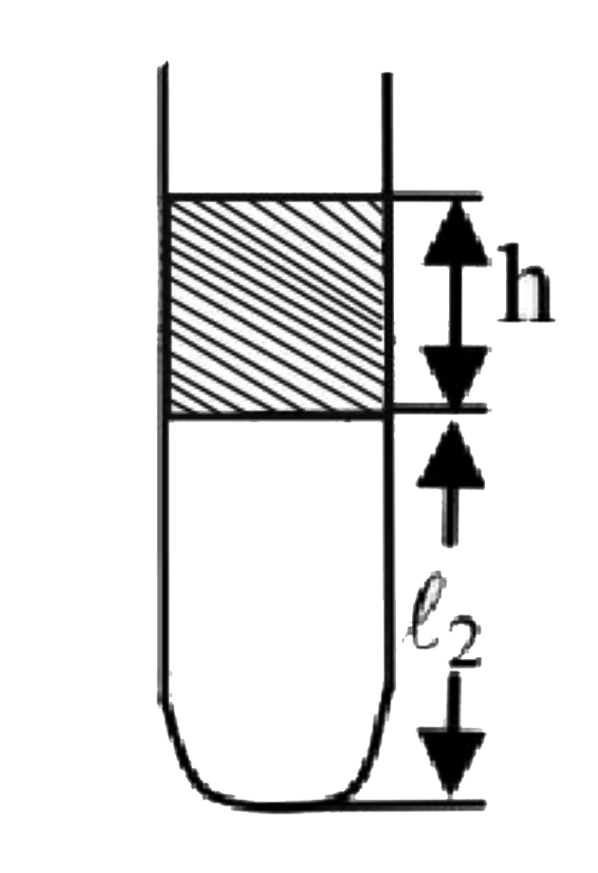
View SolutionA narrow uniform glass tube contains air enclosed by 15 cm long thread of mercury. When the tube is vertical with open end uppermost, the air column is 30 cm long. When the tube is inverted, the length of air column becomes 45 cm. Calculate the atmospheric pressure.
View Solution