Figure shows a rope of variable mass whose linear mass density is given by , λ=Ax , where A is + ve constant and x is distance from left end . It b is placed on a smooth horizontal surface . A force F is acting on it as shown .
(i) Find total mass of the rope .
(ii) Find tension at point P.
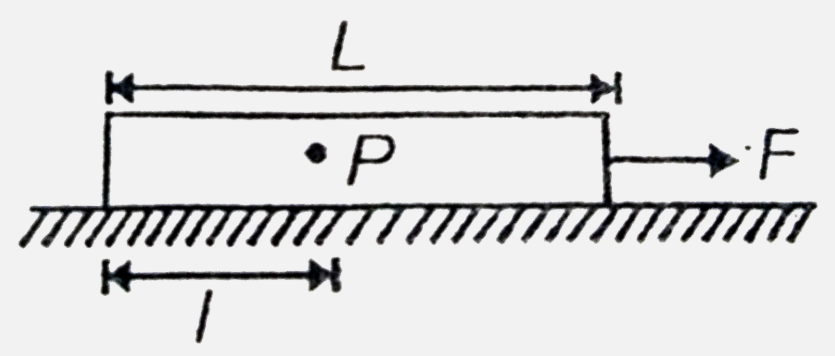
(i) Consider a differential element of thickness dx at a distance from left end . Let its mass be dm .
Now, dm=λdx=Axdx
Total mass, M∫dm=AL∫0xdx
M=AL22
(ii) Net acceleration of the rope is
a=FM=2FAL2
For system (1)
T=m1a=Al22×2FAL2
T=m1a=Al22×2FAL2 ⎡⎢⎣∵ Here m1=i∫0λdx=i∫0Axdx⎤⎥⎦
⇒T=Fl2L2

Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - Illustration
5 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - TRY YOURSELF
67 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTECHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTECHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
Find coordinates of mass center of a non-uniform rod of length L whose linear mass density lambda varies as lambda=a+bx, where x is the distance from the lighter end.
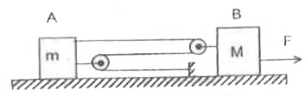
View SolutionTwo blocks A and B of masses m and M are attached with ideal string and pulley, and placed on smooth horizontal surface. Force F is applied horizontally as shown in figure. Find the ratio of the acceleration of A to that of B.
View Solution
Knowledge Check
The adjacent figure shows a non-uniform metre stick AB having the linear mass density variation λ=λ0x , where λ0 is a constant and x is the distance from end A, placed on a smooth horizontal surface. In the first experiment, the rod is pivoted at A and force F is applied perpendicular to the rod at the other end B and in the second experiment, the rod is pivoted at B and the force is applied perpendicular to the rod at the end A. If in the first case angular acceleration is αA and in the second case it is αB then
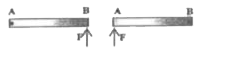 AαA=αBBαA>αBCαA<αBDdata insufficient to determine
AαA=αBBαA>αBCαA<αBDdata insufficient to determineA rope of length 5 m has uniform mass per unit length. λ=2kgm The rope is pulled by a constant force of 10N on the smooth horizontal surface as shown in figure The tension in the rope at x = 2 m from polit A is
A2 NB8 NC6 ND5 NFind centre of mass of given rod of linear mass density λ=(a+b(xl)2) , x is distance from one of its end. Length of the rod is l.
A3l4(3a+b2a+b)B3l4(2a+b3a+b)Cl4(2a+b3a+b)Dl(2a+b3a+b)
A non-uniform rope of mass M and length L has a variable linear mass density given by μ=kx, where x is the distance from one end of the wire and k is constant.
t=√(pML/9F) where F (constant) is the tension in the wire then and p
View SolutionA non-uniform wire of length l and mass M has a variable linear mass density given by μ=kx, where x is distance from one end of wire and k is a constant. Find the time taken by a pulse starting at one end to reach the other end when the tension in the wire is T.
View SolutionThe linear density of a thin rod of length 1m lies as λ=(1+2x), where x is the distance from its one end. Find the distance of its center of mass from this end.
View SolutionBlock A of mass 1kg is placed on the rough surface of block B of mass 3kg. Block B is placed on smooth horizontal surface. Blocks are given the velocities as shown. Find net work done by the frictional force. [in (−)veJ].
 .
.
View SolutionA rope of length L has its mass per unit langth λ varies according to the function λ(x)=ex/L. The rope is pulled by a constant force of 1 N on a smooth horizontal surface. The tension in the rope at x=L/2 is :

View Solution
