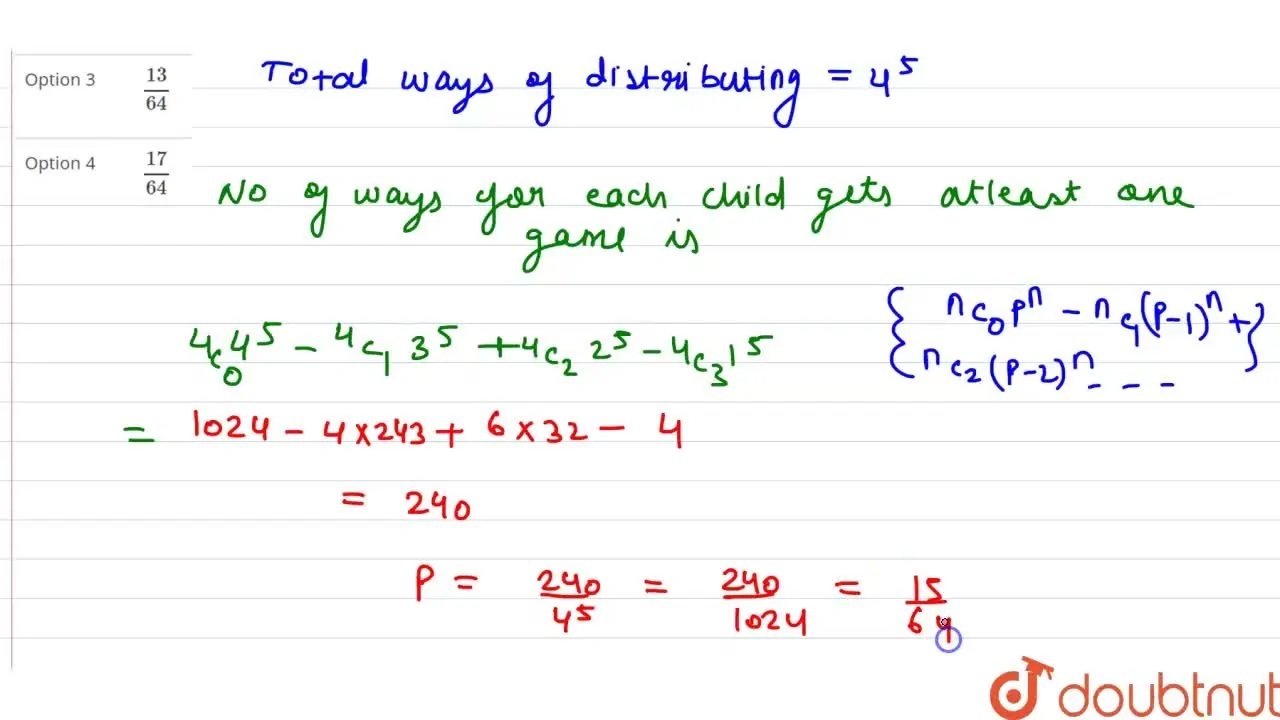5 different games are to be distributed among 4 children randomly. The probability that each child gets atleast one game is
14
1564
1364
1764
The correct Answer is:B
Step by step video, text & image solution for 5 different games are to be distributed among 4 children randomly. The probability that each child gets atleast one game is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - AAKASH INSTITUTECHAPTER - PROBABILITYEXERCISE - ASSIGNMENT (SECTION - C Objective Type Questions (More than one options are correct))21videos
PROBABILITY
- BOOK - AAKASH INSTITUTECHAPTER - PROBABILITYEXERCISE - ASSIGNMENT (SECTION - D Linked Comprehension Type Questions)21videos
PROBABILITY
- BOOK - AAKASH INSTITUTECHAPTER - PROBABILITYEXERCISE - ASSIGNMENT (SECTION - A Competition Level Questions)114videos
PROBABILITY
- BOOK - AAKASH INSTITUTECHAPTER - PRINCIPLE OF MATHEMATICAL EXERCISE - Section-D:(Assertion-Reason Type Questions)12videos
PRINCIPLE OF MATHEMATICAL
- BOOK - AAKASH INSTITUTECHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Assignment (Section - J) Aakash Challengers Questions8videos
RELATIONS AND FUNCTIONS
Similar Questions
Five different games are to be distributed among 4 children randomly. The probability that each child get at least one game is a. 1/4 b. 15/64 c. 5/9 d. 7/12
View SolutionIf 4 different biscuits are distributed among 3 children at random, the probability that the first child receives exactly one biscuit is
View SolutionIf 12 identical coins are distributed among three children at random. The probability of distributing so that each child gets atleast two coins is k then 312k7 is
View SolutionThe number of ways in which 10 identical apples can be distributed among 6 children so that each child receives atleast one apple is :
View SolutionEighteen rupee coins are distributed among 6 children at random in such a way that each child receives atleast one coin. Find the probability that the total number of coins received by first five children is atleast 8 and atmost 12.
View SolutionIf n toys are distributed among N boys randomly, then the probability that a particular boy gets r(<n) toys is
View SolutionThe total number of ways in which 11 identical apples can be distributed among 6 children such that every student gets atleast one apple,is
View SolutionTwo different families A and B are blessed with equal number of children. There are 3 tickets to be distributed amongst the children of these families so that no child gets more than one ticket. If the probability that all the tickets go to children of the family B is 112 then the number of children in each family is :
View SolutionSuppose n different games are to be given to n children. In how many ways can this be done so that eactly one child gets no game.
View SolutionIn how many ways can 20 identical toys be distributed among 4 children so that each one gets at least 3 toys?
View Solution