A solid aluminium sphere and a solid copper sphere of twice the radius are heated to the same temperature and are allowed to cool under identical surrounding temperatures. Assume that the emisssivity of both the spheres is the same. Find ratio of (a) the rate of heat loss from the aluminium sphere to the rate of heat loss from the copper sphere.
(b) the rate of fall of temperature of the aluminium sphere to the rate of fall of temperature of the copper sphere.
The specific heat copacity of aluminium =900Jkg−1.∘C−1 . and that of copper =390Jkg−1.(∘)C−1 . The density of copper =3.4 times the density of aluminium.
The correct Answer is:(a) 1:4
(b) 2.9:1
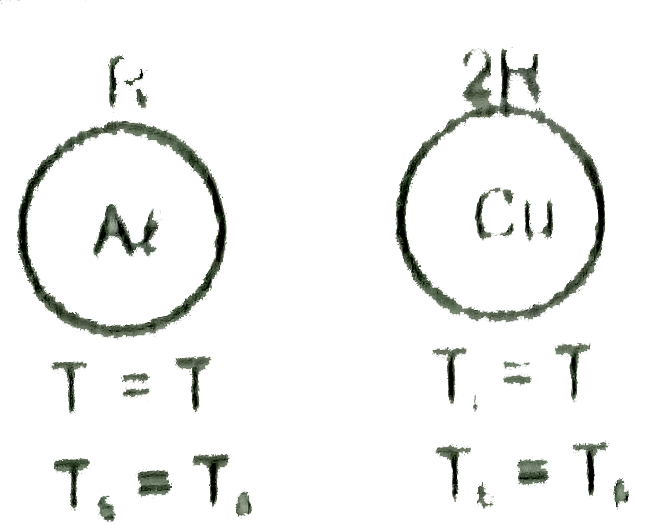
C-cooling rate H− heat loss
HAlHCu=σAAI(TAI4−T40)σeACu(TCu4−T40)
at t=0TAl=TCu=T=AAlACu=R2(2R)2=14
(b) C− cooling rate
CAlCCu=(AAlmAlSAl)(mCuSCuACu)
=(AAlACu)(mCumAl)(SCuSAl)
=(R2R)2×{(2RR)3×3.4}×390900=2.9
Topper's Solved these Questions
Similar Questions
A solid aluminium sphere and a solid copper sphere of twice the radius are heated to the same temperature and are allowed to cool under identical surrounding temperature. Assume that the emissivity of both the spheres is the same. Find the ratio of
(a) the rate of heat from the aluminium sphere to the rate of heat loss from the copper sphere and
(b) the rate of fall of temperature of the the aluminium sphere to the rate of fall temperature of teh copper sphere. The specific heat capacity of aluminium =900J/kg−∘C and that of copper =390J/kg−∘C. The density of copper is 3.4 times the density of aluminium.
View SolutionA solid aluminium sphere and a solid copper sphere of twice the radius are heated to the same temperature and are allowed to cool under identical surrounding temperatures. Assume that the emissivity of both the spheres is the same. Find ratio of (a) the rate of heat loss from the aluminium sphere to the rate of all of temperature of the copper sphere. The specific heat capacity of aluminium =900Jkg−1^(@)C^(-1).andtˆofcopper=390Jkg^(-1)^(∘)C−1 . The density of copper =3.4 times the correct wattage.
View Solution
Knowledge Check
A solid sphere and a hollow sphere of the same material and of equal radii are heated to the same temperature.
ABoth will emit equal amount of radiation per unit time in the beginning.BBoth will absorb equal amount of radiation from the surrounding in the beginning.CThe initial rate of cooling (dTdt) will be the same for the two spheres.DThe two spheres will have equal temperature at any instant.A solid sphere and a hollow sphere of the same material and of equal radii are heated to the same temperature
Aboth will emit equal amount of radiation per unit time in the beginningBboth will absorb equal amount of radiation per second from the surroundings in the beginningCthe initial rate of cooling will be the same for both the spheresDthe two spheres will have equal temperatures at any instantA solid sphere and a hollow sphere of the same material and size are heated to the same temperature and allowed to cool in the same surroundings. If the temperature difference between the surroundings and each sphere is T, then :
AThe hollow sphere will cool at a faster rate for all values of TBThe solid sphere will cool at a faster rate for all values of TCBoth spheres will cool at the same rate for all values of TDBoth spheres will cool at the same rate only for small values of T
Two spheres of same material and radius r and 2r are heated to same temperature and are kept in identical surroundings, ratio of their rate of loss of heat is
View SolutionWhen a sphere, a cube and a thin plate are heated to same temperature and then allowed to cool, the first to cool is
View SolutionWhen a sphere, a cube and a thin plate are heated to same temperature and then allowed to cool, the first to cool is
View SolutionA solid sphere of radius R and a hollow sphere of inner radius R/2 and outer radius R, made of copper ,are heated to the same temperature and are allowed to cool in the same environment .Then
View SolutionA solid sphere and a hollow sphere are heated the same temperature . Point out the true statement.
View Solution
