If rod is initially compressed by Δl length then what is the strain on the rod when the temperature
(a) is increased by Δθ (b) is decreased by Δθ
(a) Strain =Δll+αΔθ (b) Strain =∣∣∣Δll−αΔθ∣∣∣
Topper's Solved these Questions
- CALORIMETRY AND THERMAL EXPANSIONBook:RESONANCEChapter:CALORIMETRY AND THERMAL EXPANSIONExercise:Board Level Exercise
Explore 19 Videos
- CALORIMETRY AND THERMAL EXPANSIONBook:RESONANCEChapter:CALORIMETRY AND THERMAL EXPANSIONExercise:Exercise-1
Explore 1 Video
- CALORIMETRY AND THERMAL EXPANSIONBook:RESONANCEChapter:CALORIMETRY AND THERMAL EXPANSIONExercise:Solved miscellaneous problems
Explore 1 Video
- CALORIMETRYBook:RESONANCEChapter:CALORIMETRYExercise:Exercise
Explore 19 Videos
- CAPACITORBook:RESONANCEChapter:CAPACITORExercise:Exercise
Explore 45 Videos
Similar Questions
A brass rod of length 1m is fixed to a vertical wall at one end, with the other end keeping free to expand. When the temperature of the rod is increased by 120∘C, the length increases by 3cm. What is the strain?
View SolutionIn which case will the efficiency of a carnot cycle be higher : When the hot body temperature is increased by ΔT, or when the cold body temperature is decreased by the same magnitude ?
View Solution
Knowledge Check
Temperature of plate is increased by Δθ then find new
 Ainner radiusBouter radiusCthe difference in outer and inner radius and show that it is positiveDarea of plate meterial (assume coefficient of expansion is α)
Ainner radiusBouter radiusCthe difference in outer and inner radius and show that it is positiveDarea of plate meterial (assume coefficient of expansion is α)The value of a is numerically equal to the percentage change in length when the temperature of the rod is increased by
A1∘CB1KC273 CD100∘CThe moment of inertia of a rod about its perpendicular bisector is I . When the temperature of the rod is increased by ΔT , the increase in the moment of inertia of the rod about the same axis is (Here , α is the coefficient of linear expansion of the rod )
AαIΔTB2αIΔTCαIΔT2D2IΔTα
The moment of inertia of a rod about its perpendicular bisector is l, when temperature of rod is increased by ΔT, the increase in the moment of inertia of the rod about same axis (γ = temperature coefficient of volume expansion)
View SolutionThe system shown in figure consists of three springs and two rods as shown. If the temperature of the rods is increased by δ(t) calculate the energy stored in each of the springs. The springs are initially relaxed. There is no friction.
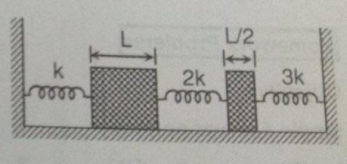
View SolutionFind the equillibrium length for the system after increasing temperature by ΔT.
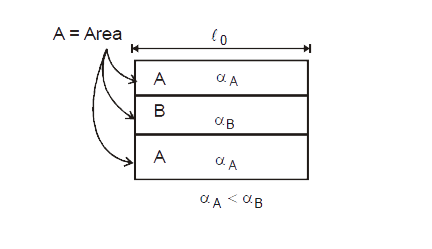
View SolutionA rod has length L0 at a reference temperature T0, coefficient of linear expansion α, Young's modulus Y, area of cross section A. Rod lie unconstrained on a smooth surface temperature of rod is increased bby ΔT. Mark the correct statement
View SolutionA unifrom rod is fixed at one end to a rigid support, its temperture is gradually increased the representaion of graph strain (e) versus increment in temperature Δθ is
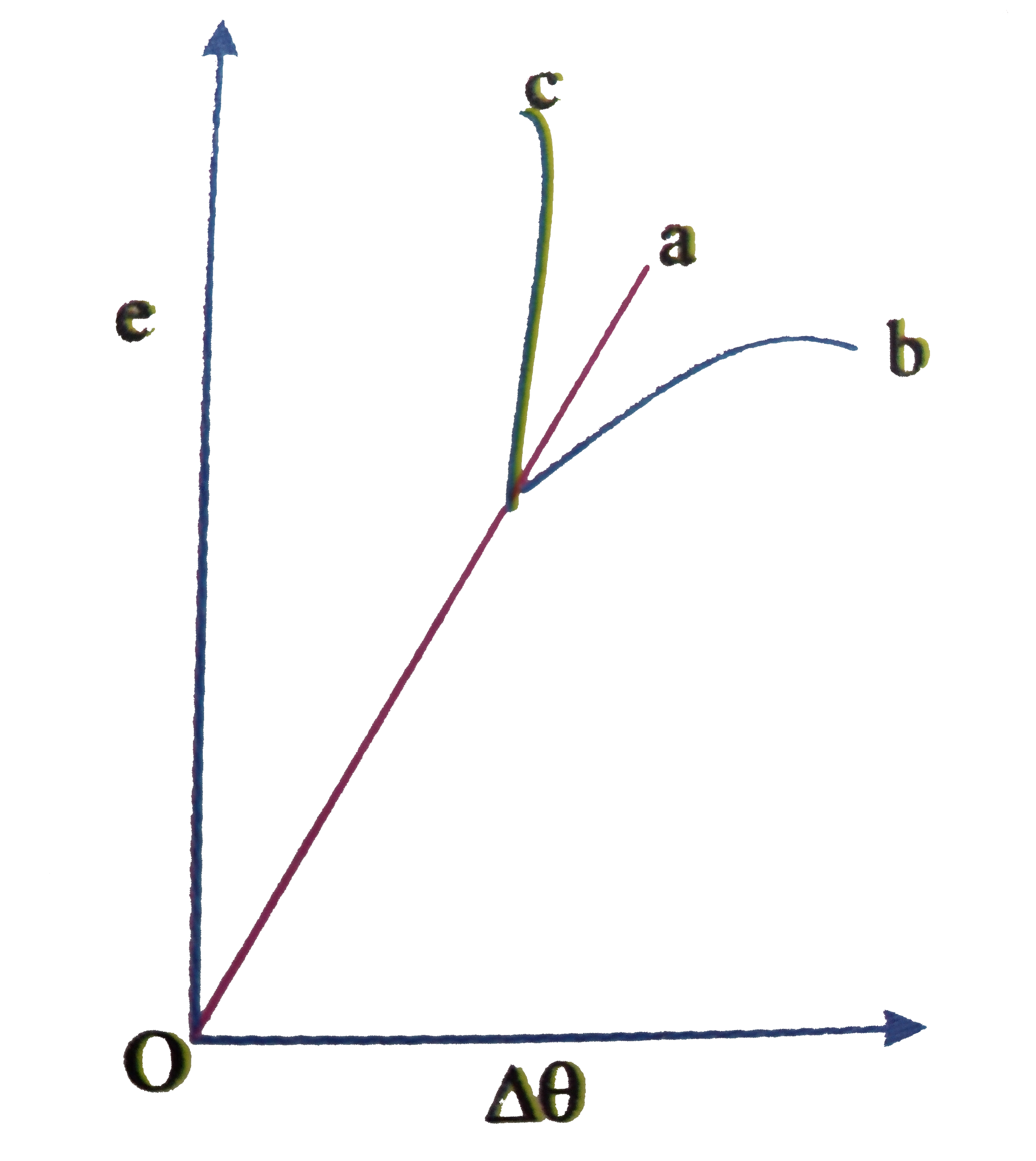
View Solution

