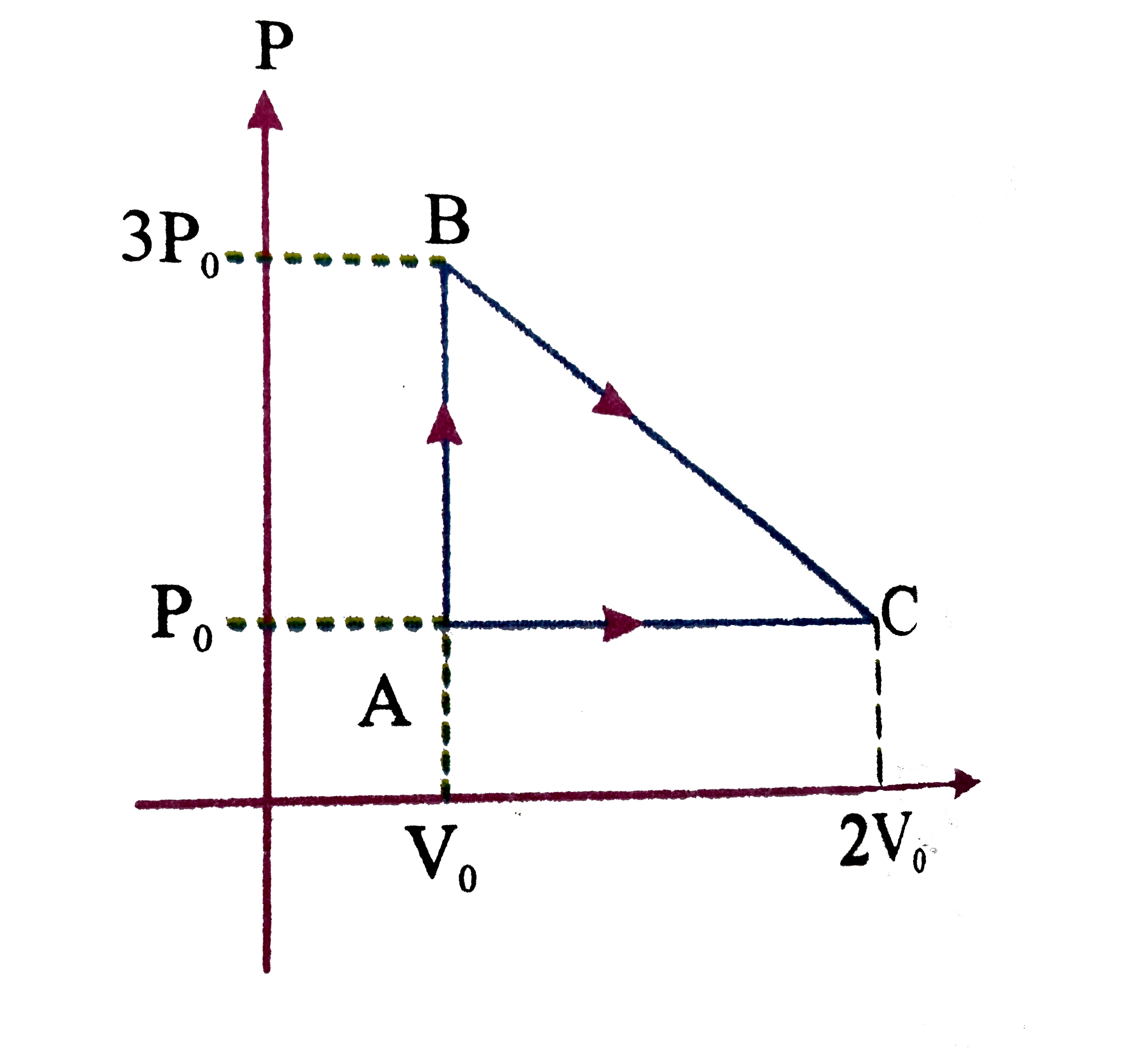
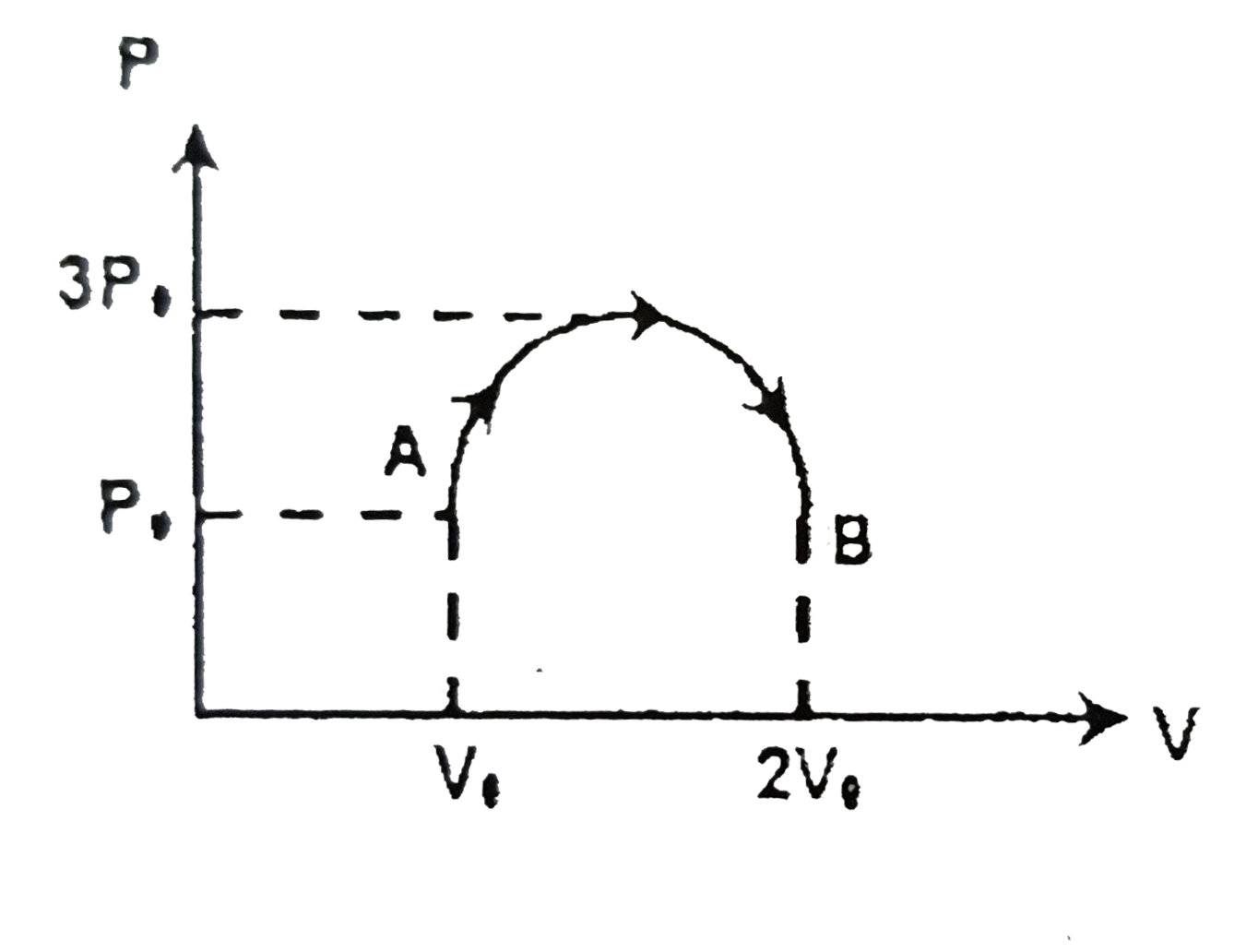
One mole of an ideal monoatomatic gas is taken round the cylic process ABCA as shown Then
the work doen by the gas
the heat rejected by the gas in the path CA and the heat absorbed by the gas in the path AB
the net heat absorbed by the gas in the path BC,
the maximum temperature attained by the gas during the cycle.
The correct Answer is:A, B, C, D
ABCA is a clockwise cyclic process.
∴ Work done by the gas
W=+ Area fo triangle ABC
=12(base)(height)
=12(2V0−V0)(3P0−P0)
W=P0V0

(b) Number of moles n=1 and gas monoatomic, therefore
CV=(3/2)R and CP=(5/2)R
⇒CVR=32 and CPR=52
Heat rejected in path CA: (process is isobaric)
∴dQCA=CpdT=CP(TA−TC)
=CP(PAVAR−PCVCR)−CPR(PAVA−PCVC)
Subsituting the values
dQCA=52(P0V0−2P0V0)=−52P0V0
Therefore, heat rejected in the process CA is 52P0V0
Heat absorbed in path AB: (process is isochoric)
∴dQAB=CVdT.
=CV(TB−TA)
=CV(PBVBR−PAVAR)=CVR(PBVB−PAVA)=32(PBVB−PAVA)
=32(3P0V0−P0V0)
dQAB=3P0V0
∴ Heat absorbed in the process Ab is 3P0V0
(c) Let dQBC be the heat absorbed in the process BC,
Total heat absorbed, dQ=dQCA+dQAB+dQBC
dQ=(−52P0V0)+(3P0V0)+dQBC
dQ=dQBC+P0V02
Change in internal energy, dU=0
∴dQ=dW
∴dQBC+P0V02=P0V0
∴dQBC=P0V02
∴ Heat absorbed in the process BC is P0V02
∴BC=P0V02
(d) Maximum temperature of the gas will be somewhere between B and C. Line BC is a straight line. Therefore P−V equation for the process BC can be written as:
P=−mV+c
(y=mx+c)
Here m=2P0V0 and C=5P0
P=−(2P0V0)V+5P0
Multiplying the equation by V.
PV=−(2P0V0).V2+5P0V
(PV=RTforn=1)
R=−(2P0V0)V2+5P0V
or T=1R[5P0V−2P0V0V2]...(1)
For T to be maximum, dTdV=0
5P0−4P0V0.V=0V=5V04
i.e at V=5V04, (on line BC) temperature of the gas is maximum. From equation (1), this maximum temperature will be
Tmax=1R[5P0(5V04)−(2P0V0)(5V04)2]
⇒Tmax=258P0V0R
Topper's Solved these Questions
- KTG & THERMODYNAMICSBOOK - RESONANCECHAPTER - KTG & THERMODYNAMICSEXERCISE - Advancel Level Problems
1 Video
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - RESONANCECHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Exercise
64 Videos
- MAGNETIC FIELD AND FORCESBOOK - RESONANCECHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Exercise
65 Videos
Similar Questions
One mole of an ideal monatomic gas is taken round the cyclic process ABCA as shown in figure. Calculate
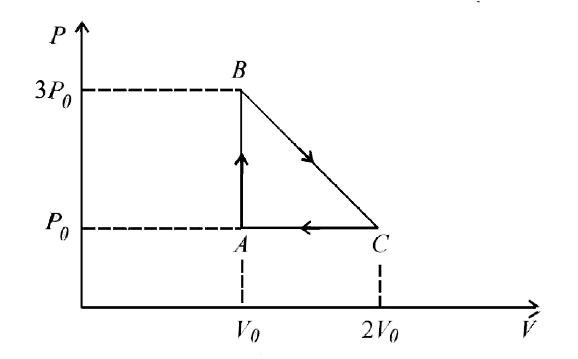
(a) the work done by the gas.
(b) the heat rejected by the gas in the path CA and the heat absorbed by the gas in the path AB,
(c) the net heat absorbed by the gas in the path BC,
(d) the maximum temperature attained by the gas during the cycle.
View SolutionOne mole of ideal monoatomic gas is taken round the cyclic process as shown in figure.
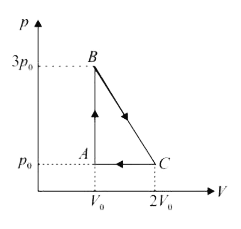
The heat rejected by the gas in the path is ………...and the heat absorbed by the gas in the path AB is ………...........
View Solution
Knowledge Check
One mole of an ideal mono-atomic gas is taken round cyclic process ABCD as shown in figure below. Calculate
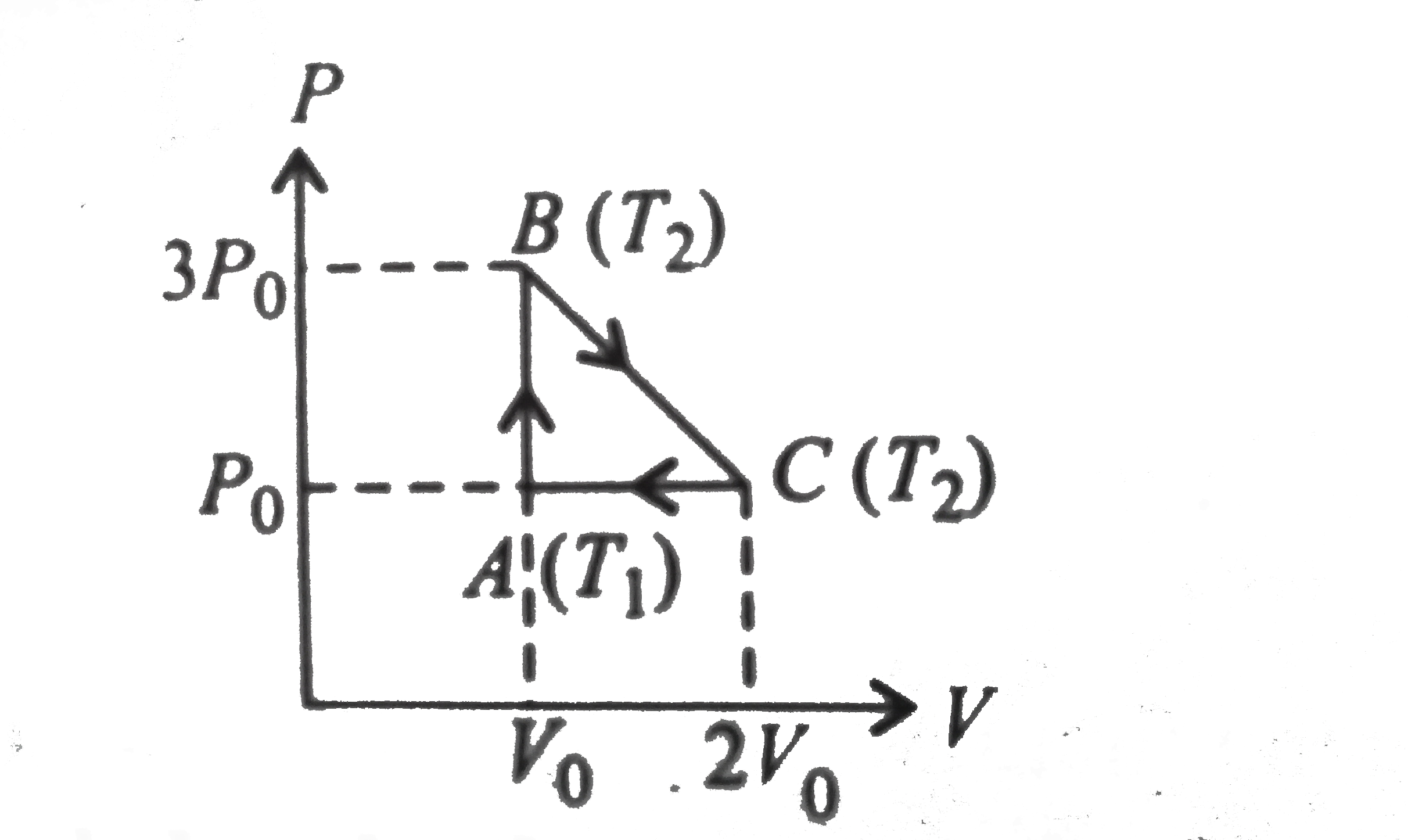 AThe work done by the gas.BThe heat rejected by the gas in the path CAand the heat absorbed by the gas in the path AB.CThe net heat absorbed by the gas in the path BC.DThe maixmum temperature attained by the gas during the cycle.
AThe work done by the gas.BThe heat rejected by the gas in the path CAand the heat absorbed by the gas in the path AB.CThe net heat absorbed by the gas in the path BC.DThe maixmum temperature attained by the gas during the cycle.One mole of an ideal monoatomic has is taken through cyclic process ABC as shown in the graph with pressure and temperature as coordinate axes. Process AB is defined as PT = constant. Take universal gas constant to be R. Then:
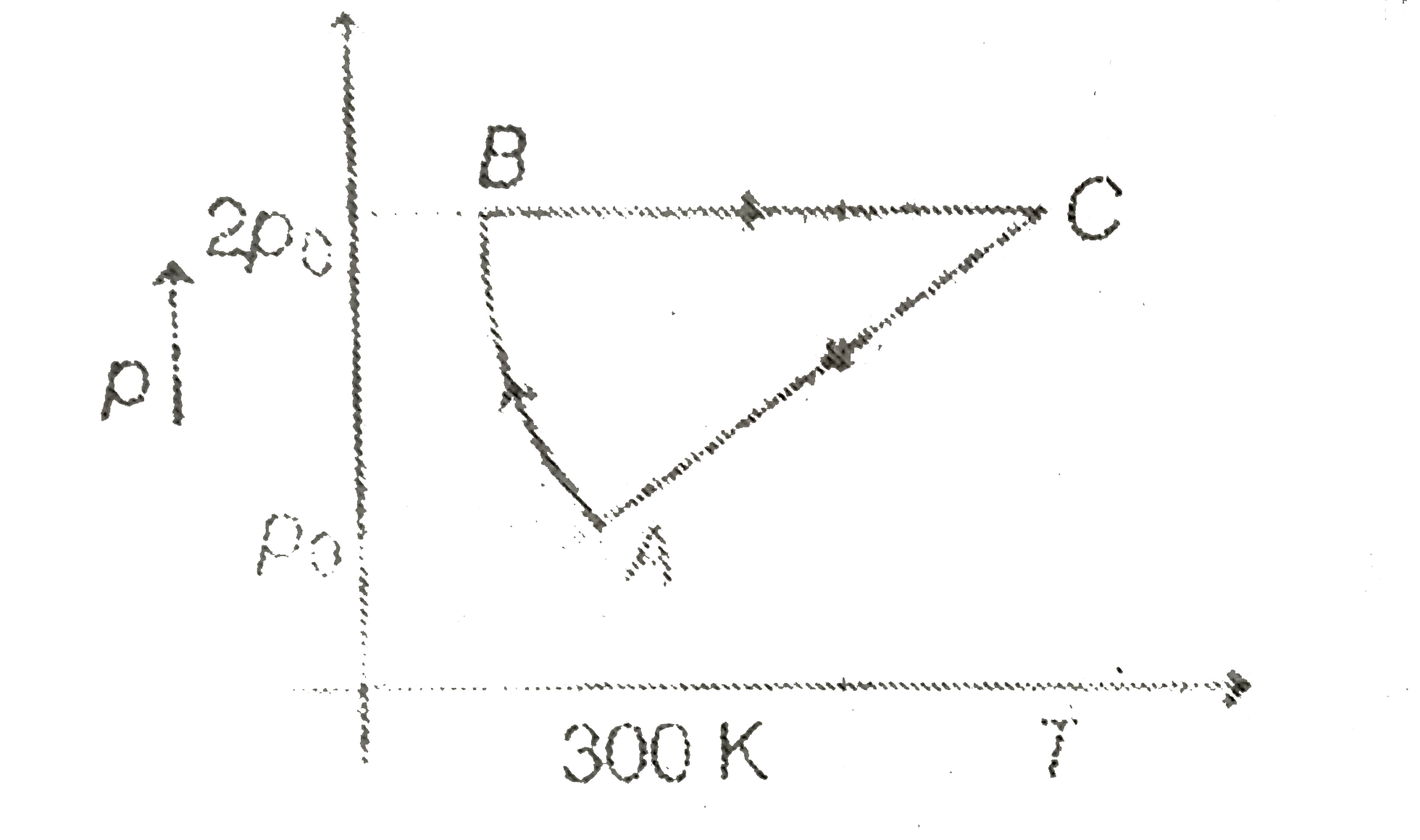
Change in internal energy of gas in the process CA isA−350RB−450RC−550RD−600ROne mole of an ideal monoatomic has is taken through cyclic process ABC as shown in the graph with pressure and temperature as coordinate axes. Process AB is defined as PT = constant. Take universal gas constant to be R. Then:
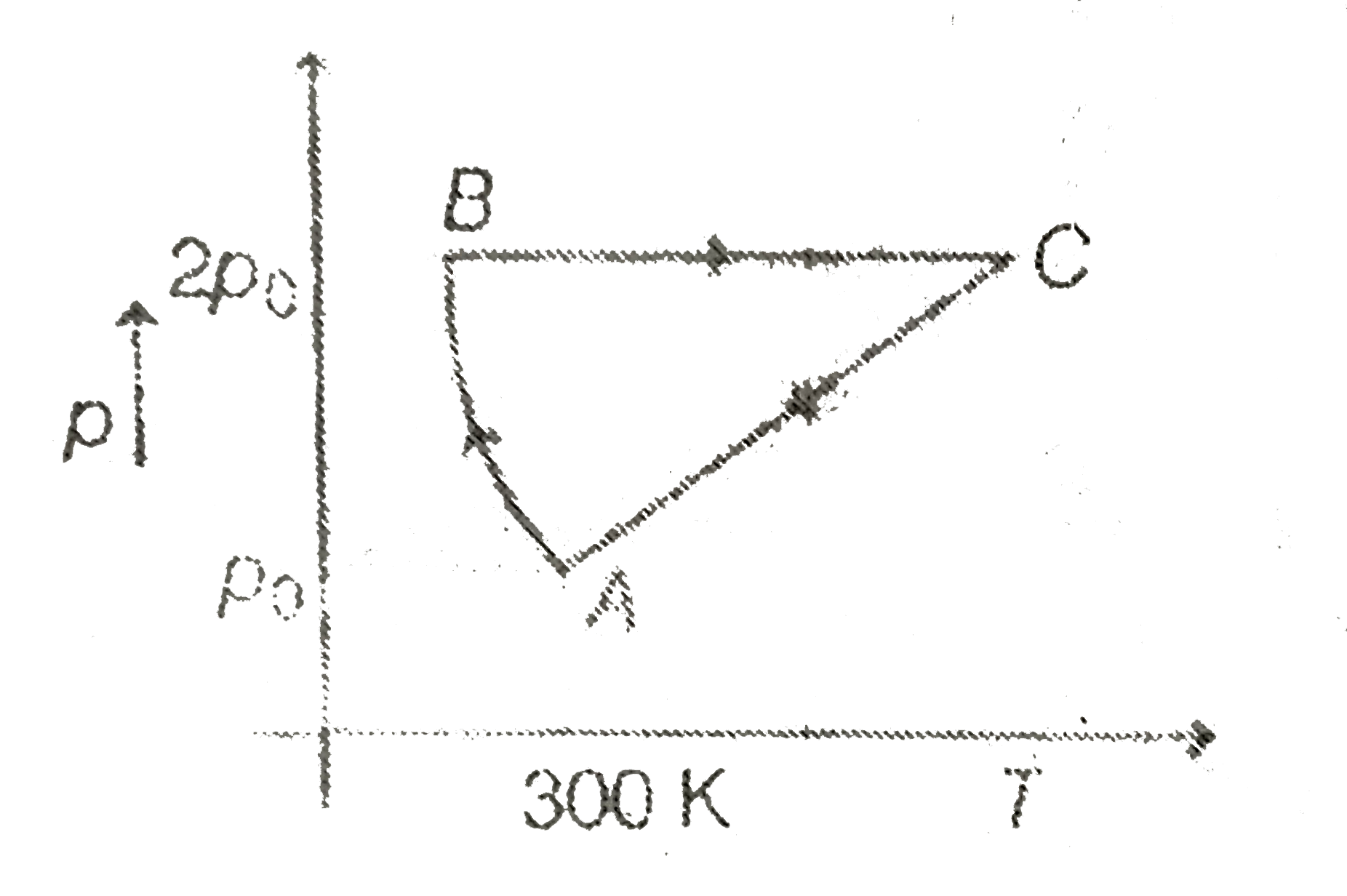
work done on gas in the process AB isA675 RB975 RC300 RD600 R
One mole of ideal monatomic gas in taken in cyclice process ABCA as shown in the figure

Calculate :
(a) The work done by the gas
(b) The heat rejected by the gas in the path CA
(c) The net heat absorbed be the by gas in the path BC
(d) Maximum temperature obtained by the gas during the cycle.
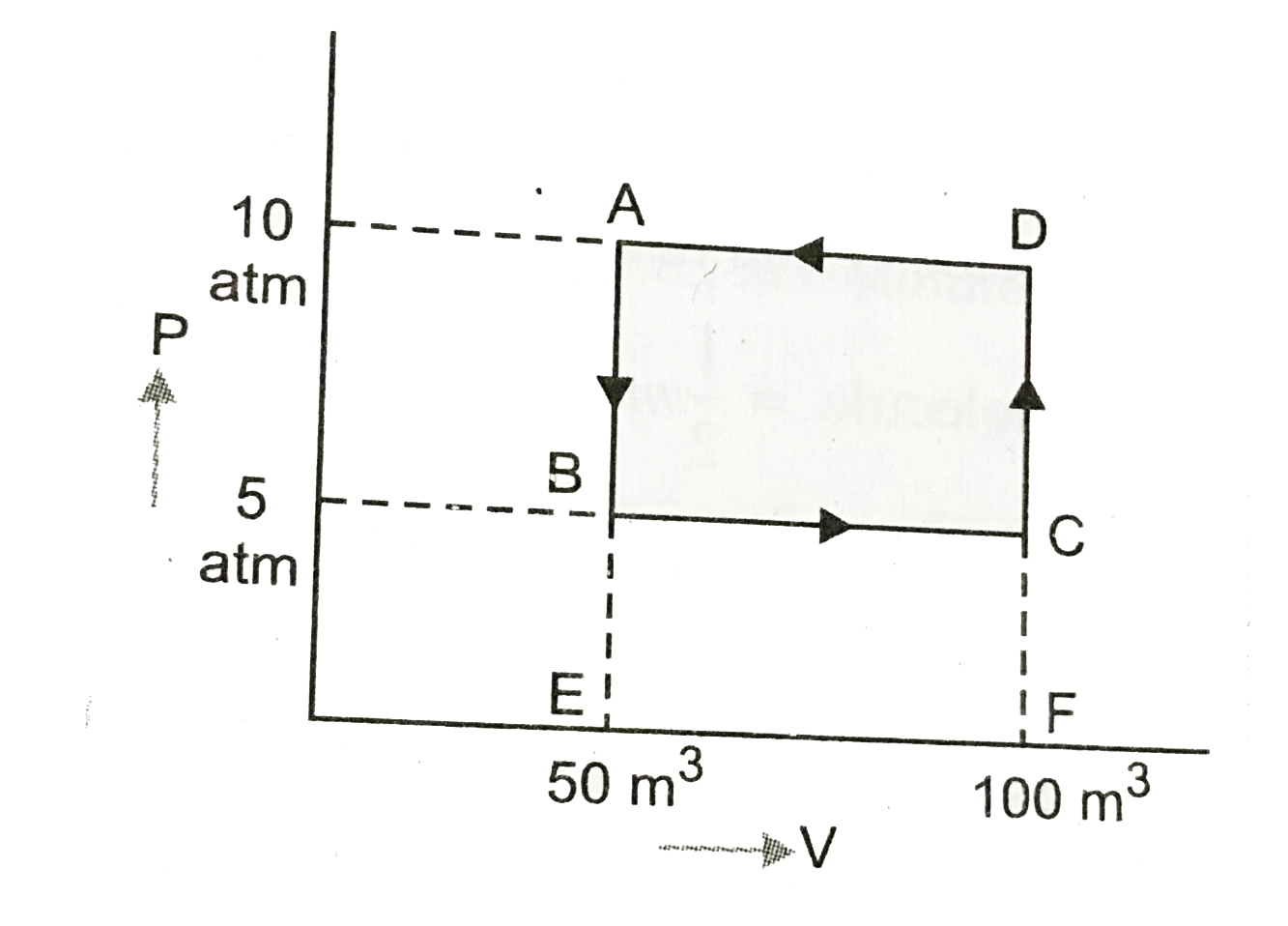
View SolutionOne mole of an ideal gas is taken through the cyclic process ABCDA, as shown in (figure). Using the graph, calculate
(i) Work done in the processes A→B,B→C,C→DandD→A
(ii) Work done in complete cycle ABCDA
(iii) Heat rejected by the gas in one complete cycle.
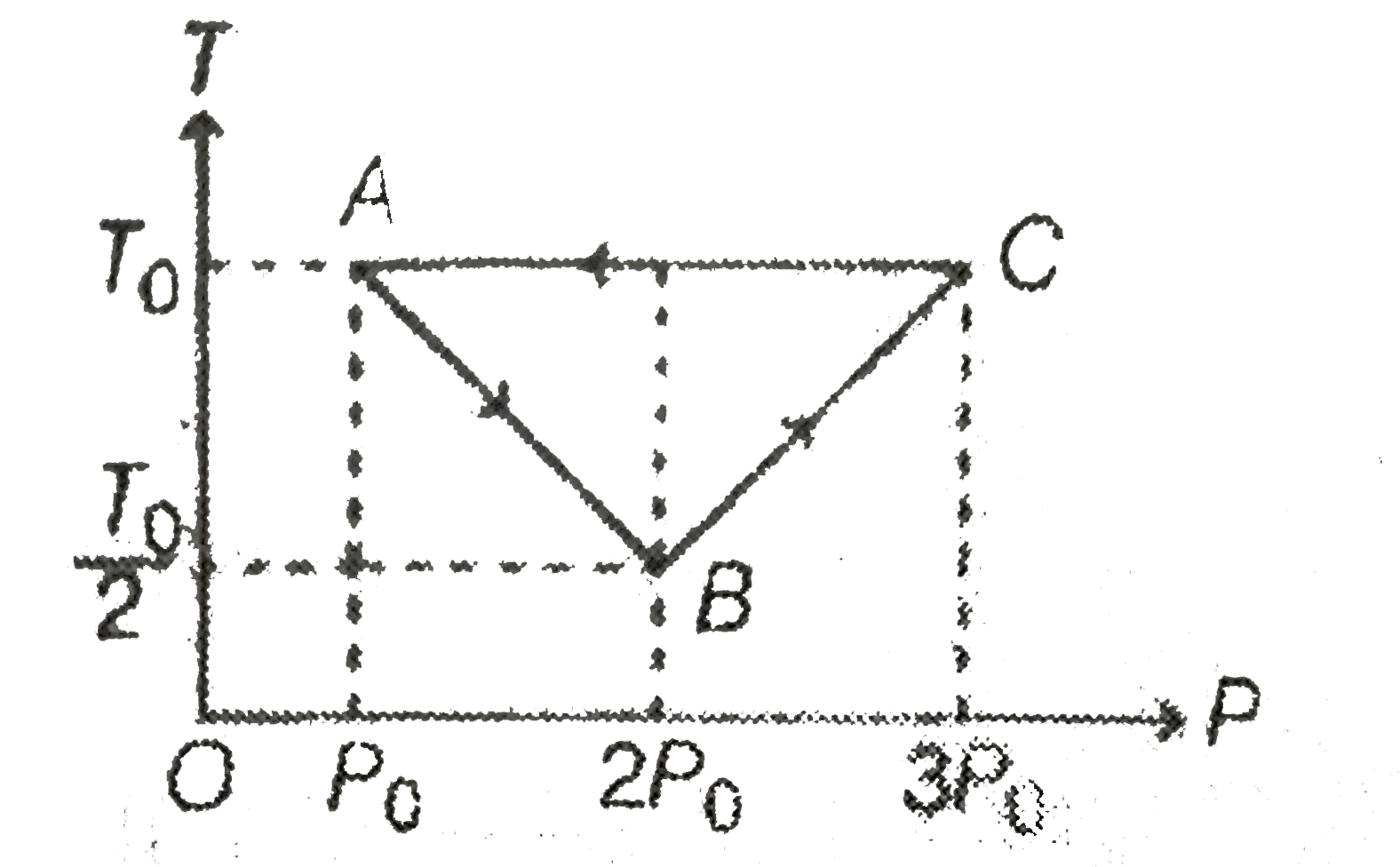
View SolutionOne mole of an ideal monoatomic gas is taken through a cyclic process as shown. Choose the correct option(s).
View SolutionA sample of an ideal monoatomic gas is taken round the cycle ABCA as shown in the figure the work done during the cycle is

View SolutionOne mole of an ideal monoatomic gas is taken through the thermodynamic process shown in the P−V diagram. The heat supplied to the system is
View Solution