A parallel plate capacitor with circular plates of radius 1m has a capacitor of 1nF. At t=0, it is connected for charging in series with a resistor R=1MΩ across a 2V battery. Calculate the magnetic field at a point P, halfway between the cnetre and the periphery of the plates, after t=10−3sec.
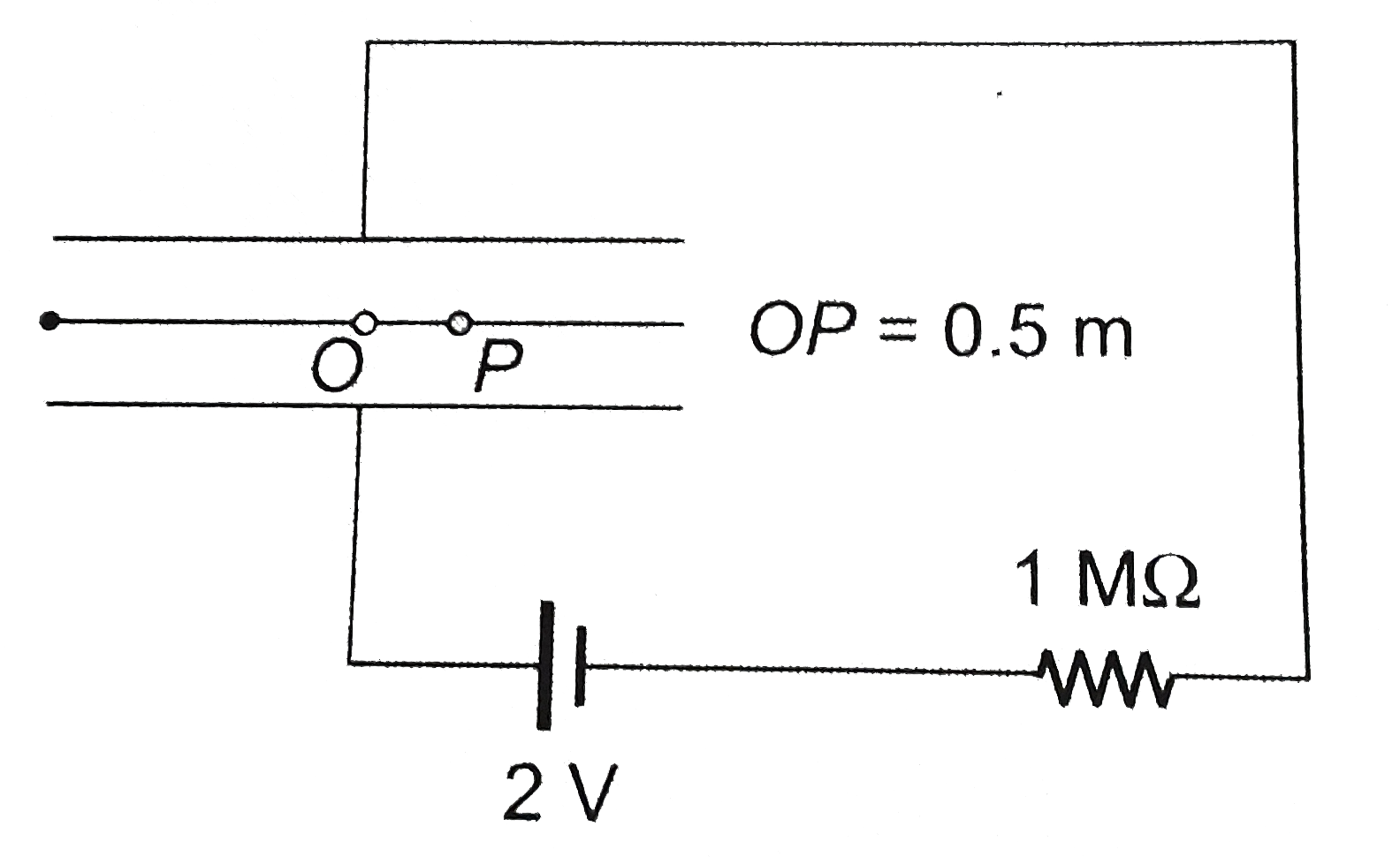
The time constant of the CR circuit is τ=CR=10−3s. Then we have
q(t)=CV[1−exp(−t/τ)]
=2×10−8[1−exp(−t/10−2]
The electric field in between the plates at time t is
E=q(t)ε0A=qπε0,A=π(1)2m2= area of the plates
Consider now a circular loop of radius (1/2)m parallel tot he plates passing through P. the magnetic field B at all points on the loop is along the loop and of the same value. the flux ΦE through this loop is
ΦE=E× area of the loop
=E×π×(12)2=πE4=q4ε0
The displacement current
id=ε0=edΦEdt=14dqdt=0.5×10−6exp(−1)
at t=10−3s. Now, applying Ampere-maxwell law to the loop we get
B×2π×(12)=π0(ic+id)=μ0(0+id)=0.5×10−6μ0exp(−1)
or, B=0.74×10−3T
Topper's Solved these Questions
- ELECTRO MAGNETIC WAVESBook:RESONANCEChapter:ELECTRO MAGNETIC WAVESExercise:Exercise
Explore 46 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCEChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 2
Explore 6 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP.No.71
Explore 1 Video
- ELECTRODYNAMICSBook:RESONANCEChapter:ELECTRODYNAMICSExercise:Advanced level problems
Explore 31 Videos
Similar Questions
A parallel plate capacitor with circular plates of radius 1m has a c apacitance of 1n F. At t=0,it is connected for charging in series with a resistance R=1MΩ across2V battery . Calculate the magnetic field at a point P, in between the plates and half way between the centre and the periphery of the plates after 10−3s.
View SolutionA parallel plate capacitor with circular plates of radius 1m has a c apacitance of 1n F. At t=0,it is connected for charging in series with a resistance R=1MΩ across2V battery . Calculate the magnetic field at a point P, in between the plates and half way between the centre and the periphery of the plates after 10−3s.
View Solution
Knowledge Check
A parallel plate capacitor has capacitance of 1.0F. If the plates are 1.0mm apart, what is the area of the plates?
A1.1×105m2B2.1×108m2C0.5×108m2D1.6×108m2Find the charge on parallel plate capacitor having circular plates of radius 8 cm and plate separation 1 mm. The potential difference is 100 V:
A1.78×10−5 CB2×10−9CC1.78×10−8CD4.3×104C
A parallel plate capacitor has circular plates of 0.08m radius and 1.0×10−3m separation If a P.D.of 100 volt is applied,the charge will be
View SolutionA parallel plate capacitor with circular plates of radius R is being charged as shown. At the instant shown, the displacement current in the region between the plates enclosed between R2 and R is given by
View SolutionA parallel plate capacitor with circular plates of radius 0.12m is being charged. A circular loop of radius 0.24 m is concentric with the capacitor and half way between the plates. The displacement current through the loop is 2.0 A. At what rate is the electric field between the plates changing?
View SolutionA parallel plate capacitor has capacitance of 1.0F. If the plates are 1.0mm apart, what is the area of the plates?
View SolutionA parallel plate air capacitor is made using two square plates each of side 0.2 m, spaced 1 cm apart. It is connected to a 50V battery.
What is the charge on each plate ?
View SolutionA parallel plate air capacitor is made using two square plates each of side 0.2 m, spaced 1 cm apart. It is connected to a 50V battery.
What is the energy stored in the capacitor ?
View Solution