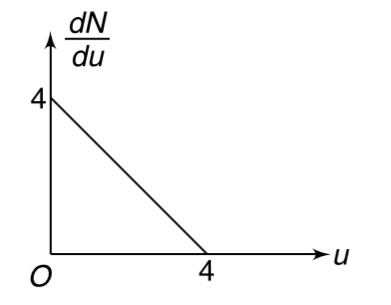
A hypothetical gas sample has its molecular speed distribution graph as shown in the figure. The speed (u) and dNdu have appropriate units. Find the root mean square speed of the molecules. Do not worry about units.
A
√53
B
√83
C
√73
D
None of these
Video Solution
Text Solution
The correct Answer is:B
The equation of the straight line is
dNdu=−u+4
u2rms=∫u2dN∫dN=4∫0u2dNdudu4∫0dNdudu
=4∫0u2(−u+4)duarea under the graph
u2rms=∫u2dN∫dN=4∫0u2dNdudu4∫0dNdudu
4∫0(−u3)du+44∫0u2du12×4×4=[−u44+4.u33]408
u2rms=83⇒urms=√83
|
Updated on:21/07/2023
Similar Questions
Knowledge Check
- Question 1 - Select One
The root mean square speed of gas molecules
Ais same for all gases at the same temperatureBdepends on the mass of the gas molecule and its temperatureCis independent of the density and pressure of the gasDdepends only on the temperature and volume of the gas - Question 2 - Select One
The root mean square speed of the molecules of a gas is
Aindependent of its pressure but directly proportional to its Kelvin temperatureBdirectly proportional to two square root of both its pressure and its Kelvin temperatureCindepdent of its pressure but directly proportional to the square root of its Kelvin temperature.Ddirectly proportional to its pressure and its Kelvin temperature. - Question 3 - Select One
Four molecules of ags have speeds 1,2,3 and 4 km/s.The volue of the root mean square speed of the gas molecules is
A12√15km/sB12√10km/sC2.56km/sD√152km/s
The ratio of the root mean square speeds of the molecules of an ideal gas at 270 K and 30 K will be _______ .
View SolutionTwo molecules of a gas have speeds of 9×106ms−1 and 1×106ms−1, respectively. What is the root mean square speed of these molecules.
View SolutionA mixture of two gases is contained in a vessel. The Gas 1 is monoatomic and gas 2 is diatomic and the ratio of root mean square speeds of the molecules of two gases is
View SolutionGraph shows a hypothetical speed distribution for a sample of N gas particle (for V>V0,dNdV=0)
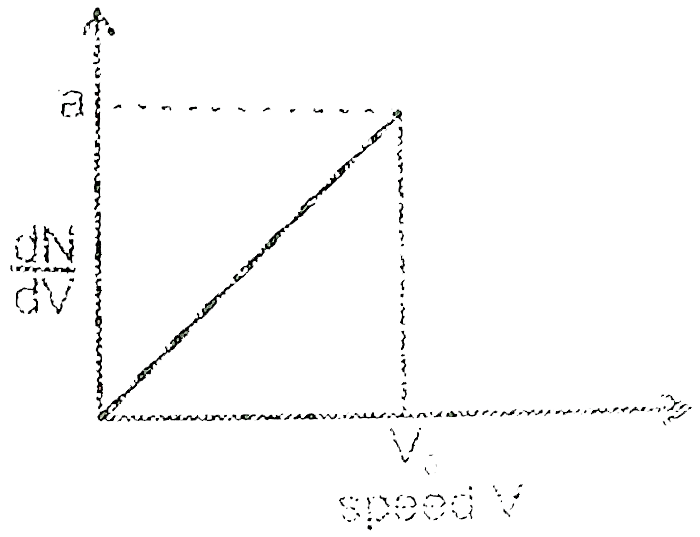 View Solution
View SolutionIn the distribution of molecular speeds of a gas is as per the figure shown below, then the ratio of the most probale, the average, and the root mean square speeds, respectively, is
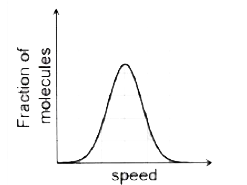 View Solution
View Solution

