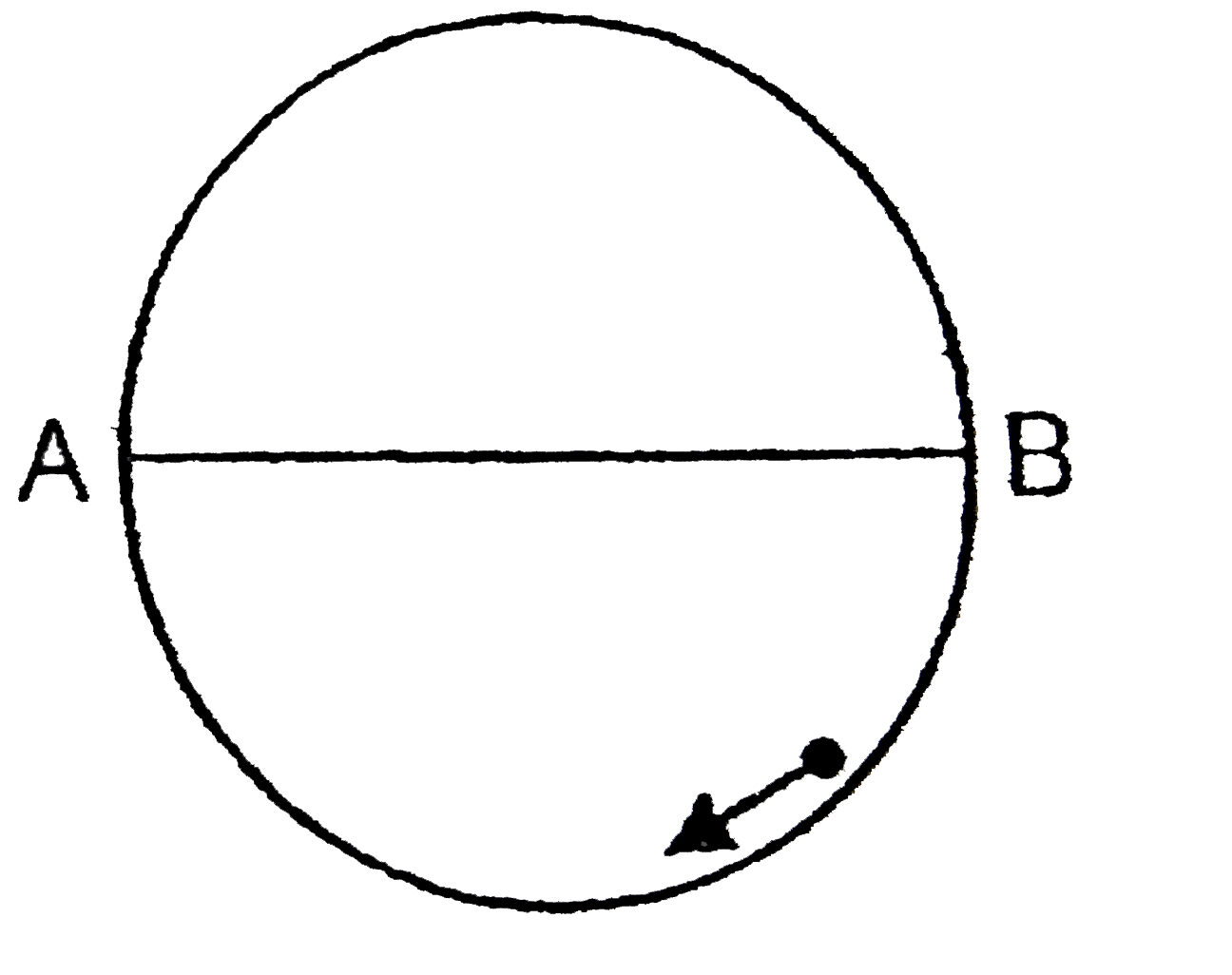
A particle of mass m oscillates inside the smooth surface a fixed pipe of radius R. The axis of the pipe is horizontal and the particle moves from B to A and back. At an instant the kinetic energy of the particle is K (say at position of the particle shown in figure ). Then choose the correct value of force applied by particle on the pipe at this instant.
KR
5KR
3KR
2KR
The correct Answer is:C
Let velocity of particle at point P be v.
From conservation of mechanical energy
12.mv2=K=mgh
Let N be the normal reaction between the particle and the pipe at this instant.
Then N−mgsinθ=mv2R
But, mv2R=2KR and sinθ=hR
Hence, N=mg(hR)+2KR=KR+2KR
('∴K=mgh)
Hence, N=3KR= force on the pipe.

Similar Questions
A graph between kinetic energy and momentum of a particle is plotted as shown in the figure. The mass of the moving particle is :

View SolutionA heavy particle of mass m is in motion on a smooth surface of hemisphere of radius R and there is no friction. At the initial instant the particle is at the topmost point A and has an initial velocity v0 At what point will the particle leave the surface of the hemisphere ? Also determine the value of v0 for which the particle will leave the sphere at the initial instant.
View Solution
Knowledge Check
A particle of mass m oscillates inside a smooth spherical shell of radius R and starts its motion from point B. At given instant the kinetic energy of the particle is K. Then the force applied by particle on the shell at this instant is :−
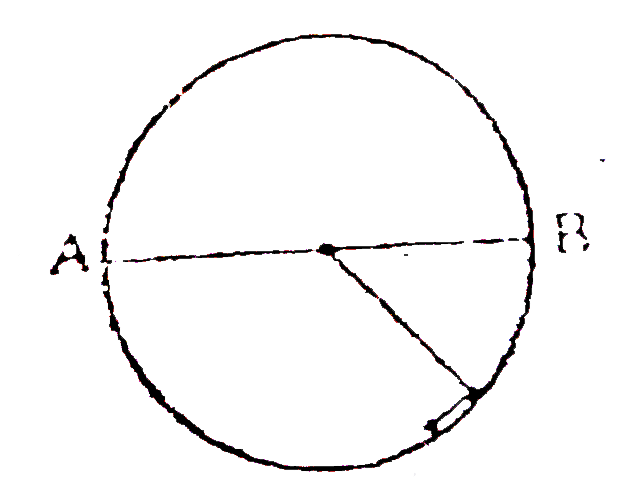 AKRB2KRC3KRDK2R
AKRB2KRC3KRDK2RThe kinetic energy K of a particle moving along x - axis varies its position (x) as shown in figure.

The magnitude of force acting on particle at x = 9m isAzeroB5 NC20 ND7.5NThe kinetic energy K of a particle moving along x axis varies with its position (x) as shown in the figure. The magnitude of force acting on particle at x = 9 m is -
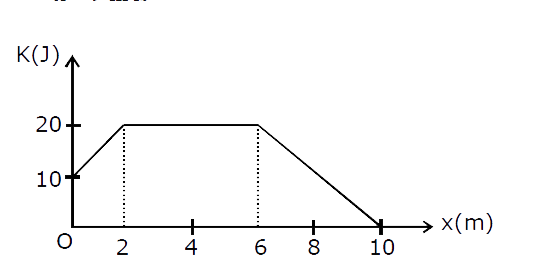 AzeroB5 NC20 ND7.5 N
AzeroB5 NC20 ND7.5 N
The kinetic energy K of a particle moving along x - axis varies with its position (x) as shown in figure

The magnitude of force acting on particle at x = 9 mis
View SolutionA particle of mass m is moved from A to B as show in figure. Then potential energy of the the particle
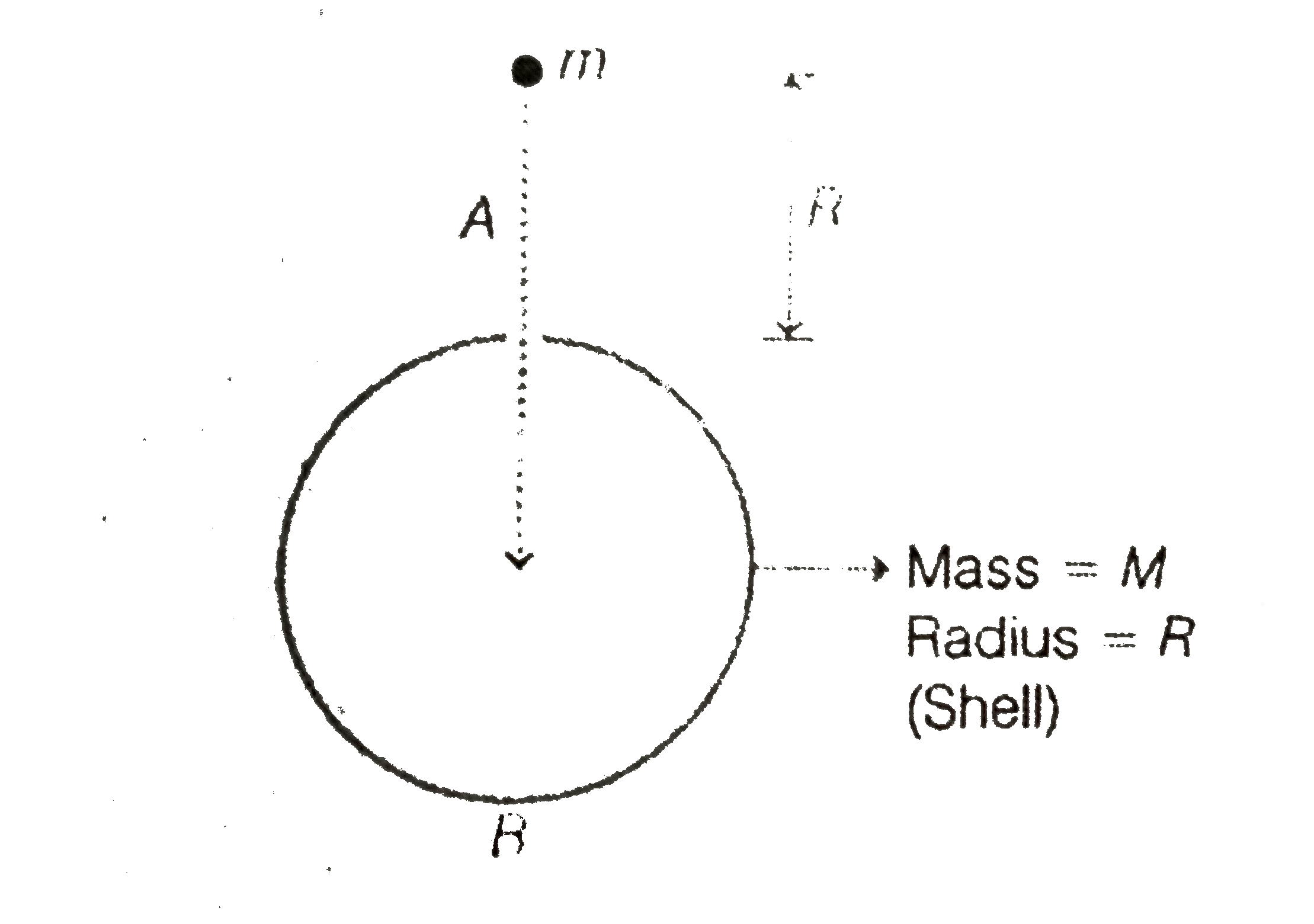
View SolutionA particle of mass m oscillates along the horizontal diameter AB inside a smooth spherical shell of radius R. At any instant K.E. of the partical is K. Then force applied by particle on the shell at this instant is:

View SolutionA particle of mass m executing S.H.M. about its mean position. The total energy of the particle at given instant is
View SolutionA particle of mass m is executing SHM about its mean position. The total energy of the particle at given instant is
View Solution