A man walking downhill with velocity V0 finds that his umbrella gives him maximum protection from rain when he holds it such that the stick is perpendicular to the hill surface. When the man turns back and climbs the hill with velocity V0, he finds that it is most appropriate to hold the umbrella stick vertical. then the actual speed of raindrops in terms of V0 is : (the inclination of the hill is θ=37∘)

√63V03
√71V03
√73V03
√87V03
The correct Answer is:C
Take x axis along the incline and y direction perpendicular to it.

Velocity of rain relative to the man is perpendicular to the incline in the case (i.e., along the umbrella stick. This keeps canopy perpendicular to the rainfull and provides maximum safety.
→Vrm=→Vr−→Vm
=(Vxˆt+Vyˆj)−(V0ˆi)=(Vx−V0)ˆi+Vyˆj
Since →Vrm has no x component.
When the man is walking up. →Vrm us directed vertically downward.
→Vrm=(Vxˆi+Vyˆi)−(V0ˆi)
=V0ˆi+Vyˆj+V0ˆi
=2V0ˆi+Vyˆj
From diagram
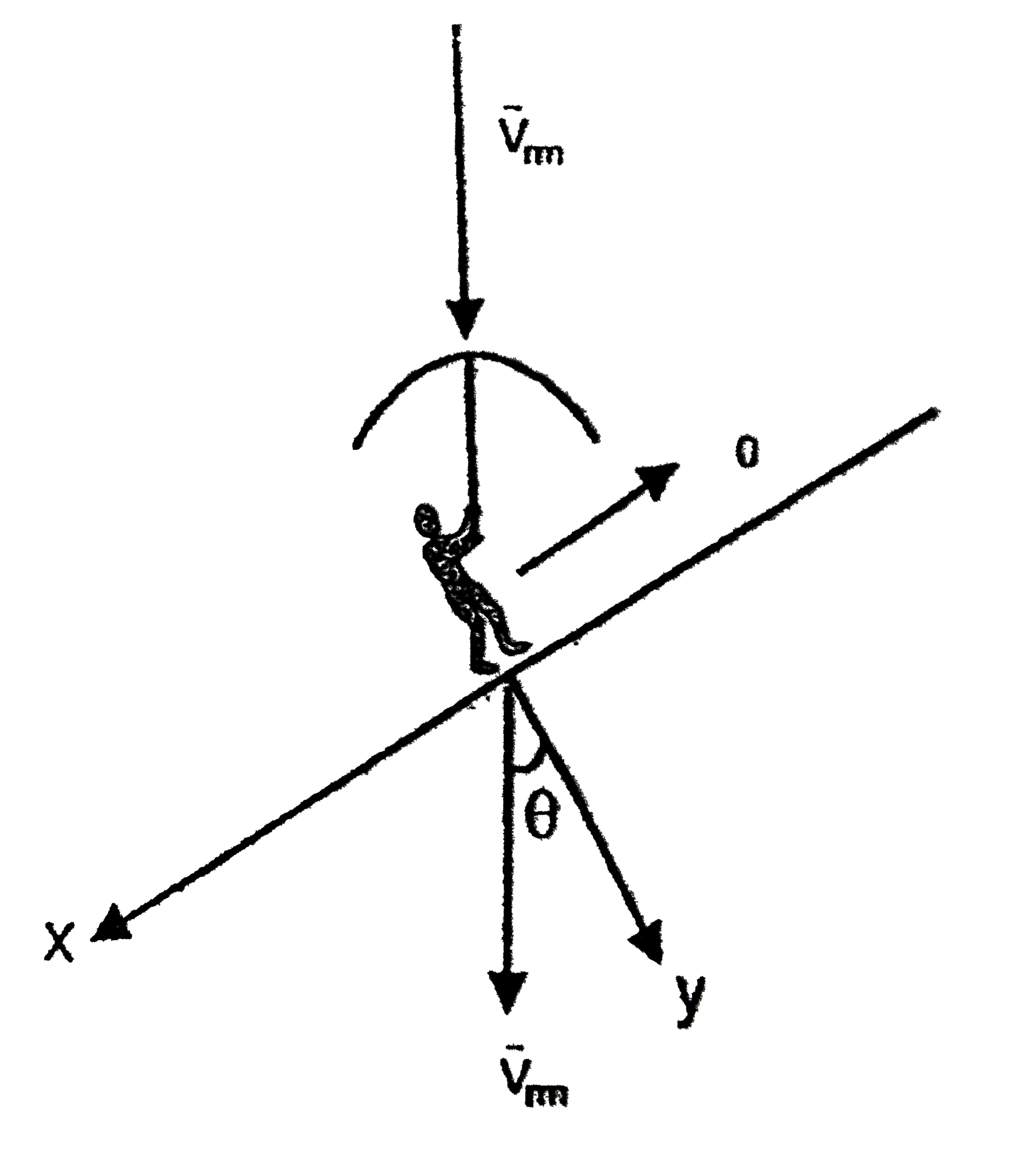
tanθ=2V0Vy
342V0Vy⇒Vy=8V03
∴Vr=√V2x+V2y=√733V0
Similar Questions
A person standing on a road has to hold his umbrella at 600 with the verticcal to keep the rain away. He throws the umbrella an starts running at 20ms−1. He finds that rain drops are hitting his head vertically. Find the speed of the rain drops wigh respect to (a) the road (b) the moving person.
View SolutionA man moving in rain holds his unbrella inclined to the vertical even though the rain drops are falling vertically downwards . Why ?
View Solution
Knowledge Check
A man runs along a horizontal road holding his umrella vertical in order to afford maximum protection form rain. The rain is actually.
AFalling verticalBComming from front of the manCComing from the back of the manDEither of (a), (b) or (c)A man moves on a cycle with a velocity of 4 km/hr. The rain appears to fall on him with a velocity of 3 km/hr vertically. The actual velocity of the rain is
A7 km/hrB5 km/hrC4/3 km/hrD3/4 km/hrRain is falling vertically and a man is moving with velocity 6ms−1. Find the angle at which the man should hold his umbrella to avoid getting wet.
Aθ=tan−1(25)Bθ=tan−1(45)Cθ=tan−1(35)Dθ=sin−1(25)
A man standing on a road has to hold his umbrella at 300 with the veetical to keep the rain away. The throws the umbrella and starts running at 10 km/h. He finds tht raindrops are hitting his head vertically. Find the speed of raindrops with respect to a. the road, b. the moving man.
View SolutionA man standing on a road has to hold his umbrella at 30∘ with the vertical to keep the rain away. He throws the umbrella and starts running at 10km/hr. He finds that rain drop are hitting his head vertically. Find the speed of rain drops with respect to (a) road (b) the moving man.
View SolutionA man running with velocity 3m/s finds that raindrops are hitting him vertically with a speed of 4m/s.
Magnitude of velocity of the raindrops is
View SolutionA Person is walking in rain feels the velocity of rain as twice to his velocity.At which angle he should hold the umbrella with vertical if he moves forward, if it is raining vertically downwards
View SolutionIf rain falls vertically with a velocity Vr and wind blows with a velocity Vw from east to west, then a person standing on the roadside should hold the umbrella in the direction
View Solution
