In adiabatic container with adiabatic piston contains 4gmN2 gas and 0.8gm He gas are separated by a weakly conducting light partition. Both piston and partition are free ro move. Initial temperature of N2 and He gases are '3T0' and 'T0' respectively. Initially system is at Rest and in equilibrium. Final temperature of the gas is.

2T0
3T02
7T04
5T02
The correct Answer is:A
In adiabatic …………..
428(7R2)(3T0−T)=(0.8)4(5R2)(T−T0)
T=2T0
Similar Questions
A gas is found to obey P2V= constant. The inital temperature and volume of gss are T0 and V0. If the gas expands to volume 3V0, then the final temperature of gas is √nT0. Find n.
View SolutionA thermally insulated vessels contains two liquids with initial temperature T1 and T2 and specific heats C0 and 2C0, separted by a non conducting partition. The partition is removed, and the difference between the initial temperature of one of the liquids and the temperature T established in the vessel turns out to be equal to half the difference between the initial temperatures of the liquids. Determine the ratio of M1/M2 of the masses of the liquids.

View Solution
Knowledge Check
A cylindrical adiabatic container of total volume 2V0 divided into two equal parts by a conducting piston which is free to move as shown in figure. Each part containing identical gas at pressure P0. Initially temperature of left and right part is 4T0andT0 respectively. An external force is applied on the piston of area 'A' to keep the piston at rest. The value of external force required when thermal equilibrium is reached is.
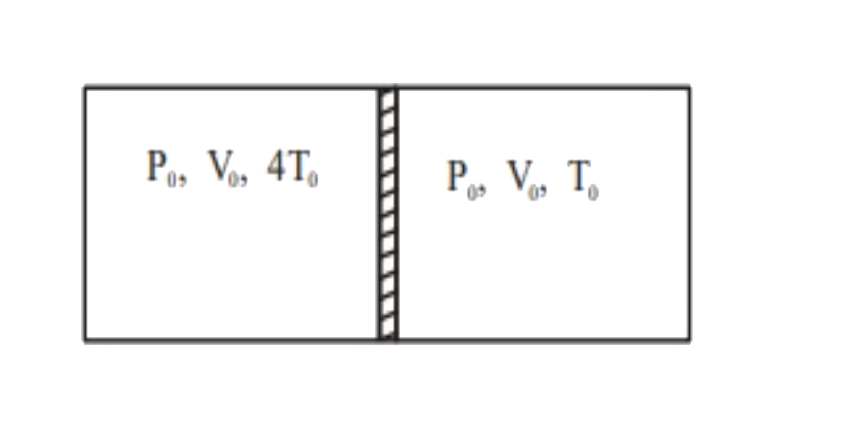 A85P0AB25P0AC56P0AD65P0A
A85P0AB25P0AC56P0AD65P0AIn an adiabatic expansion of a gas initial and final temperatures are T1and T2 respectively, then the change in internal energy of the gas is
ARλ(T2−T1)BRλ−1(T1−T2)CR(T1−T2)DZeroA gas is found to obey the law P2V=constant. The initial temperature and volume are T0andV0. If the gas expands to a volume 3V0, its final temperature becomes
AT03BT0√3C3T0D√3T0
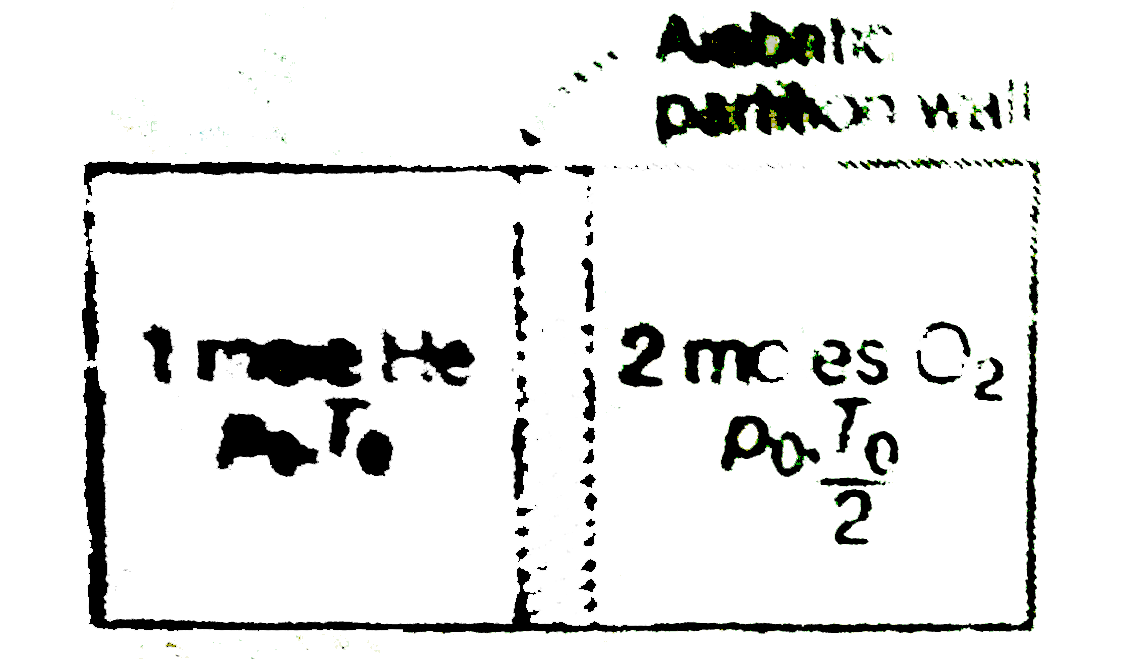
Consider the adjacent figure. A piston divides a cylindrical container into two equal parts. The lets part contains 1 mole of helium gas and the right part contains two moles or oxygen gas. The initial temperatures and pressures of the gases in the left chamber are T0 and p0 and the right chamber are T02 and p0 respectively as shown in the figure. The piston as well as the walls of the container are adiabatic. After removal of the piston, gases mix homoganeously and the final pressure becomes p=4n13p0. Find the value of n.
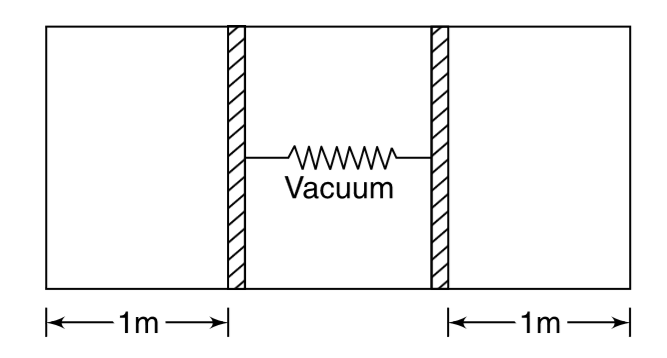
View SolutionA cylindrical container is divided into three parts by two tight fitting pistons. The pistons are connected by a spring. The region between the pistons is vacuum and the other two parts have same number of moles of an ideal gas. Initially, both the gas chambers are at temperature T0 and the spring is compressed by 1 m. Length of both gas chambers is 1 m in this position. Now the temperature of the left and right chambers are raised to 4T03 and 5T03 respectively. Find the final compression in the spring in equilibrium. Assume that the pistons slide without friction
View SolutionA gas is found to obey the law p2V = constant. The initial temperature and volume are T0 and V0 . If the gas expands to a volume 3V0, its final temperature becomes
View SolutionA gas is found to obey the law P2V= constant. The initial temperature and volume are T0 and V0∘ If the gas expands to a volume 3V0, then
View SolutionTen moles of a diatomic perfect gas are allowed to expand at constant pressure. The initial volume and temperature are V0 and T0 respectively. If 72RT0 heat is transferred to the gas, then the final volume and temperature are
View Solution