If the segment between thelines x+6y−13=0 and x−y+3=0 is bisected at (6,8) then length of segment is :
A
√268
B
√244
C
√212
D
√252
Video Solution
Text Solution
The correct Answer is:B
If the segment ………….
Let the segment is AB as shown in the figure.
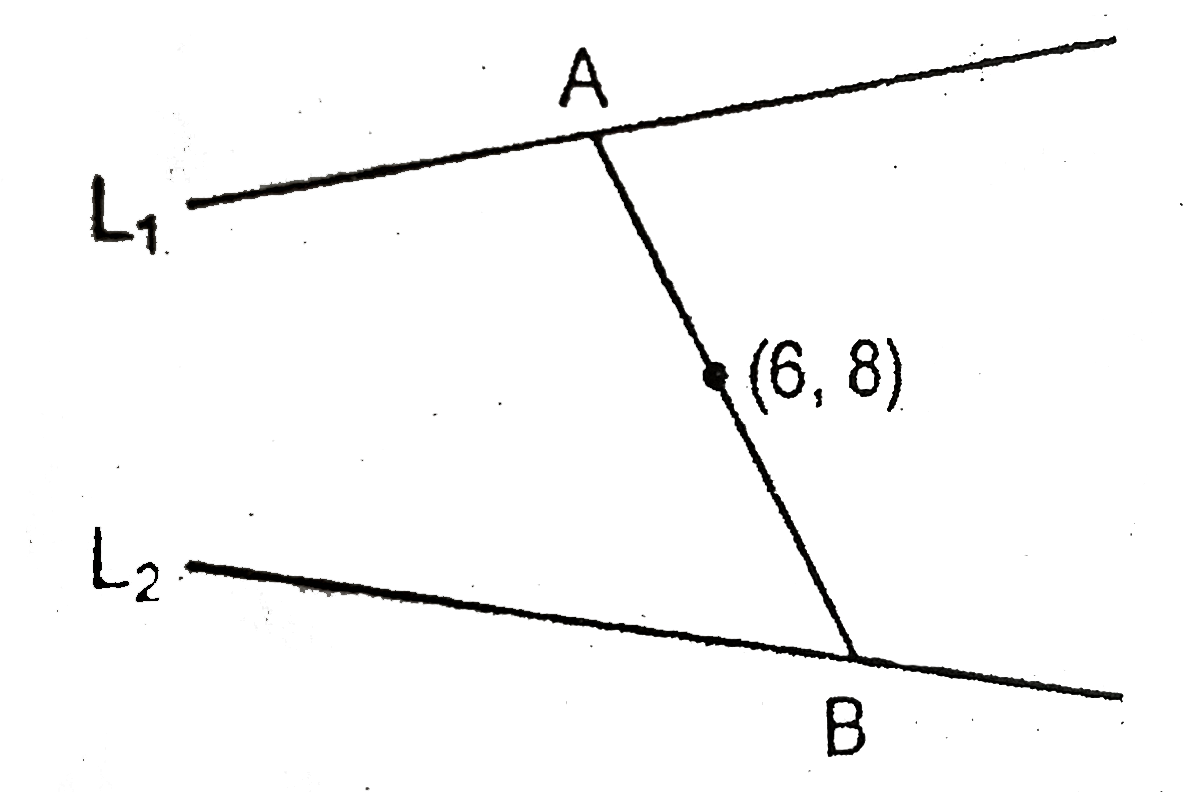
Let A=(13−6y1,y1)
B=(y2−3,y2)
∵ mid point of AB=(5,8)
∴13−6y1+y2−32=6 ....(i)
and y1+y22 .....(ii)
on solving (i) and (ii)
A=(1,2)
B=(11,14)
LAB=√244
|
Topper's Solved these Questions
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:PART : 1MATHEMATICS SEC - 1
Explore 1 Video
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:PART : 1MATHEMATICS
Explore 9 Videos
- TEST PAPERBook:RESONANCEChapter:TEST PAPERExercise:CHEMISTRY
Explore 37 Videos
- TEST SERIESBook:RESONANCEChapter:TEST SERIESExercise:MATHEMATICS
Explore 131 Videos
Similar Questions
Knowledge Check
If the segment intercepted between the lines x+6y−13=0andx−y+3=0 is bisected at (6, 8), then the square of the length of segment is
A268B244C212D252If the segment of the line between the lines x−y+2=0 and x+y+4=0 is bisected at the origin, equation of the line is
Ay+3x=0Bx+3y=0Cy−3x=0Dx−3y=0A line is such that its segment between the straight lines 5x−y−4=0and3x+4y−4=0 is bisected at the point (1,5), then its equation is
A83−35y+92=0B35x−83y+92=0C35x+35y+92=0DNone of these
Find the distance between the line 3x−4y+9=0and6x−8y−17=0
View SolutionThe distance between the parallel lines 3x+4y+3=0 and 6x+8y+11=0 is
View SolutionA line is such that its segment between the lines 5x−y+4=0and 3x+4y−4=0 is bisected at the point (1, 5). Obtain its equation.
View SolutionThe equation ofthe plane which bisects the angle between the planes 3x−6y+2z+5=0 and 4x−12y+3z−3=0 which contains the origin
View SolutionA line is such that its segments between the straight lines 5x−y=4 and 3x+4y−4=0 is bisected at the point (1,5). Its equation is
View Solution