In the figure ADB & BEF are two fixed circular paths. A block of mass m enters in the tube ADB through point A with minimum velocity to reach point B. From there it moves on another circular path of radius R'. There it is just able to complete the circle.
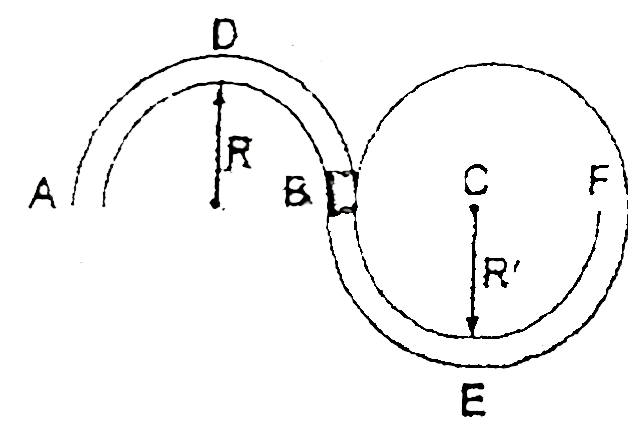
velocity at A must be √4Rg
velocity at A must be √2Rg
R'R=23
the normal reaction ast point E is 6mg
The correct Answer is:B, C, D
In the figure…………….
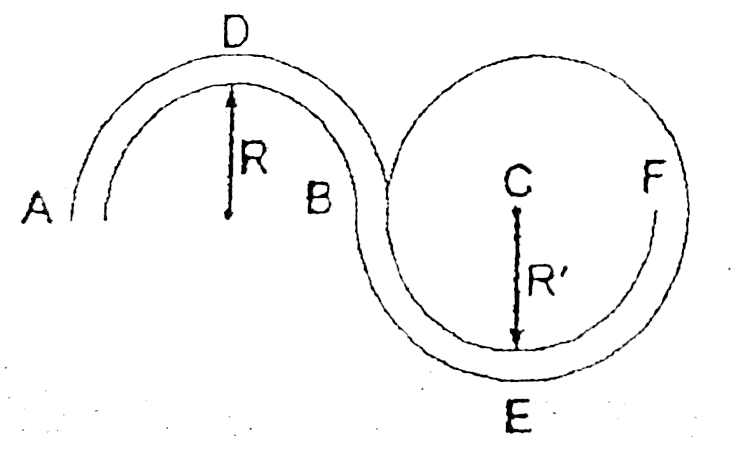
For minimum velocity at A :
12mV2A=mgR⇒VA=√2gR
Now , 12mV2B+mgR'=12mV2E
As , VB=√2gR
For looping the loop ,
VE=√5gR'
∴12m2gR+mgR'=12m5gR'
∴R'R=23
And also, N−mg=mV2ER'
N−mg=m5gR'R'
N=6mg
Similar Questions

As shown in figure BEF is a fixed vertical circular tube. A block of mass m starts moving in the tube at point B with velocity V towards E. It is just able to complete the vertical circle. Then.
View SolutionA car of maas M is moving on a horizontal circular path of radius r. At an instant its speed is v and is increasing at a rate a.
View Solution
Knowledge Check
In a vertical circle of radius r , at what point in its path a particle has tension equal to zero if it is just able to complete the vertical circle
AHighest pointBLowest pointCAny pointDAt a point horizontally from the centre of circle of radius rA particle of mass m is moving on a circular path of radius r with uniform speed v , rate of change of linear momentum is
AZeroBIndependent of speedCProportional to radius rDProportional to v2A block follows the path as shown in the figure from height h. If radius of circular path is t, then relation holds good to complete full circle is.
 Ah<5r/2Bh>5r/2Ch=5r/2Dh≥5r/2
Ah<5r/2Bh>5r/2Ch=5r/2Dh≥5r/2
Charged particle of charge q mass m moves in a circular path of radius r under the action of force F .The equivalent current is
View SolutionCharged particle of charge q mass m moves in a circular path of radius r under the action of force F .The equivalent current is
View SolutionA particle of mass 'm' is moving on a circular path of radius 'r' with uniform speed 'v'. Rate of change of linear momentum is
View SolutionA small stone of mass 200 g is tied to one end of a string of length 80 cm . Holding the other end in hand , the stone is whirled into a vertical circle What is the minimum speed that needs to be imparted at the lowest point of the circular path , so that the stone is just able to complete the vertical circle ? what would be the tension at the lowest point of circular path ? (Takeg=10m/s2) .
View SolutionA Particle of mass 'M' moves in a uniform circular path of radius 'r' with a constant speed 'v' then its centripetal acceleration is .
View Solution
