The circles $x^{2} + y^{2} - 2 x - 4 y + 1 = 0$ and $x^{2} + y^{2} + 4 y - 1 = 0$

A

touch internally

B

touch externally

C

have $3 x + 4 y - 1 = 0$ as the common tangent at the point of contact.

D

have $3 x + 4 y + 1 = 0$ as the common tangent at the point of contact.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B, C

The circles …………..
$S_{1} = x^{2} + y^{2} - 2 x - 4 y + 1 = 0$ ………..(1)
$S_{2} = x^{2} + y^{2} + 4 x + 4 y - 1 = 0$ ……… (2)
$c_{1} \equiv (1, 2)$ , $r_{1} = 2$
$c_{2} \equiv (- 2, - 2)$ , $r_{2} = 3$
$c_{1} c_{2} = \sqrt{9 + 16}$
$c_{1} c_{2} = r_{1} + r_{2}$
Hene circle touch each other extermally

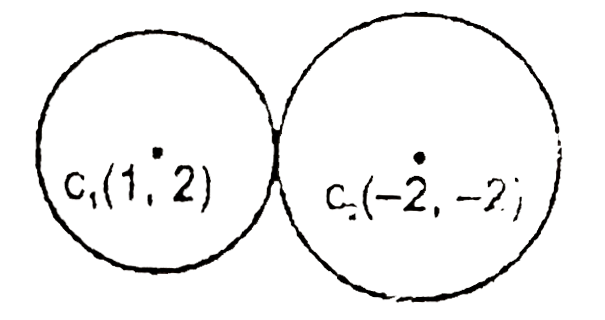
Equation of tangent at point of contact
$S_{1} - S_{2} = 0$
$6 x + 8 y - 2 = 0$
$3 x + 4 y - 1 = 0$

Updated on:21/07/2023

|

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

The length of the common chord of the circles $x^{2} + y^{2} - 2 x - 1 = 0$ and $x^{2} + y^{2} + 4 y - 1 = 0$ , is
A $\sqrt{15 / 2}$
B $\sqrt{15}$
C $2 \sqrt{15}$
Dnone of these
Two circles $x^{2} + y^{2} - 2 x - 4 y = 0$
and $x^{2} + y^{2} - 8 y - 4 = 0$
Atouch externally
Btouch internally
Cdo not touch
Dnone
The circles $x^{2} + y^{2} - 2 x - 15 = 0$ and $x^{2} + y^{2} + 4 y + 3 = 0$ have
Ano common tangent
Bone common tangent
Cthree common tangents
Dfour common tangents

RESONANCE-TEST PAPERS-MATHEMATICS

Home
Ask Doubt
Profile