A sphere of mass m and radius r is released from a wedge of mass 2m as show. ABC is hemispherical position of radius R. Find the impules imparted to the system consicting wedge and sphere by the vertical wall w1w2 till the time sphere reaches at the bottom most position of spherical portion for the first time. Friction between wedge asnd horizontal surface is absent is sufficient to avoid slipping between them.
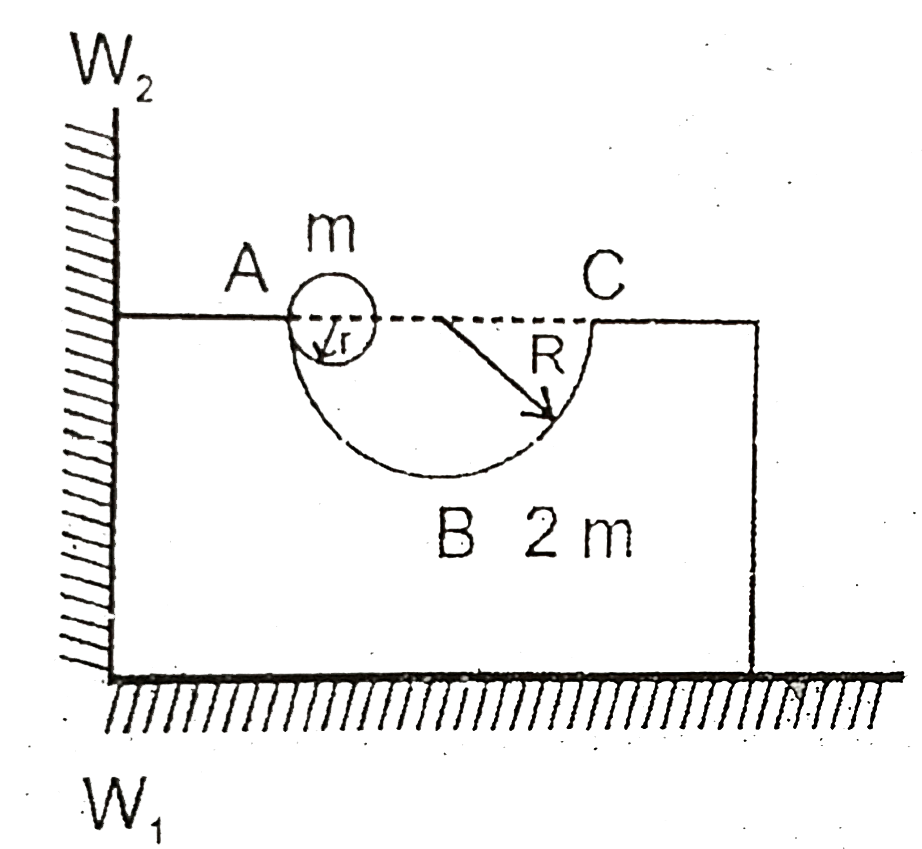
m√2g(R−r)7
m√10g(R−r)7
2m√5g(R−r)7
3m√2g(R−r)7
The correct Answer is:B
A sphere of ……………
mg(R−r)=710mV2=7P210m

P=m√10g(R−r)7 = Impulse on the system by wall
Similar Questions
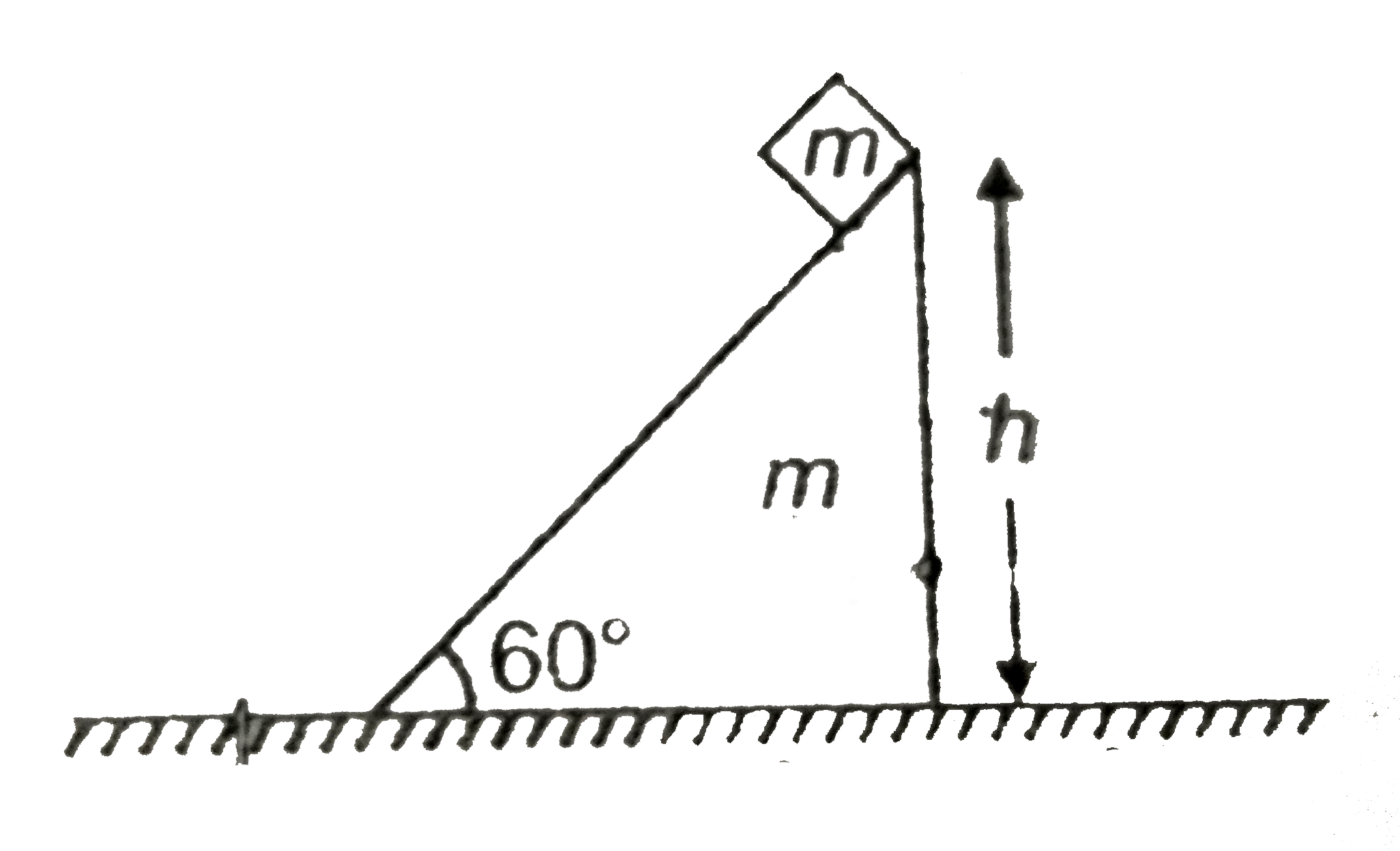
A block of mass m is released from a wedge of mass m as shown in figure . Find the time taken by the block to reach the end of the wedge.
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.

Force of friction between sphere and plank is
View Solution
Knowledge Check
A uniform solid sphere of mass m and radius r is suspended symmetrically by a uniform thin spherical shell of radius 2r and mass m.
AThe gravitational field at a distance of 1.5r from the centre is 29Gmr2BThe gravitational field at a distance of 2.5r from centre is 825Gmr2CThe gravitational field at a distance of 1.5r from centre is zeroDThe gravitational field between the sphere and spherical shell is uniform.A ball of mass m is released from A inside a smooth wedge of mass m as shown in figure. What is the speed of the wedge when the ball reaches point B?
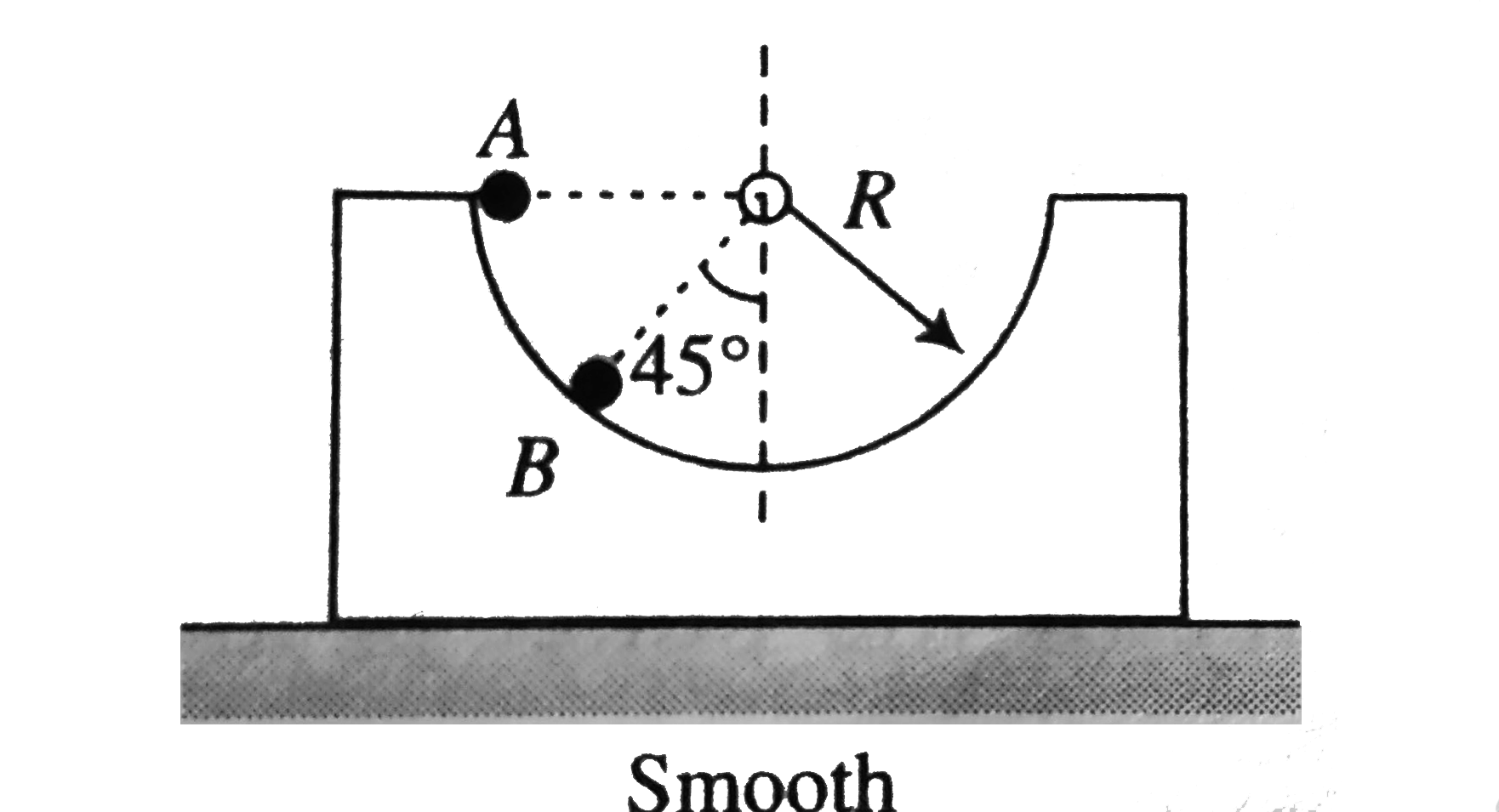 A(a) (gR3√2)1/2B(b) √2gRC(c) (5gR2√3)1/2D(d) √32gR
A(a) (gR3√2)1/2B(b) √2gRC(c) (5gR2√3)1/2D(d) √32gRThree solid spheres each of mass m and radius R are released from the position shown in figure. The speed of any one sphere at the time of collision would be
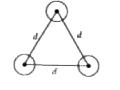 A√Gm(1d−3R)B√Gm(3d−1R)C√Gm(2R−1d)D√Gm(1R−2d)
A√Gm(1d−3R)B√Gm(3d−1R)C√Gm(2R−1d)D√Gm(1R−2d)
A solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.
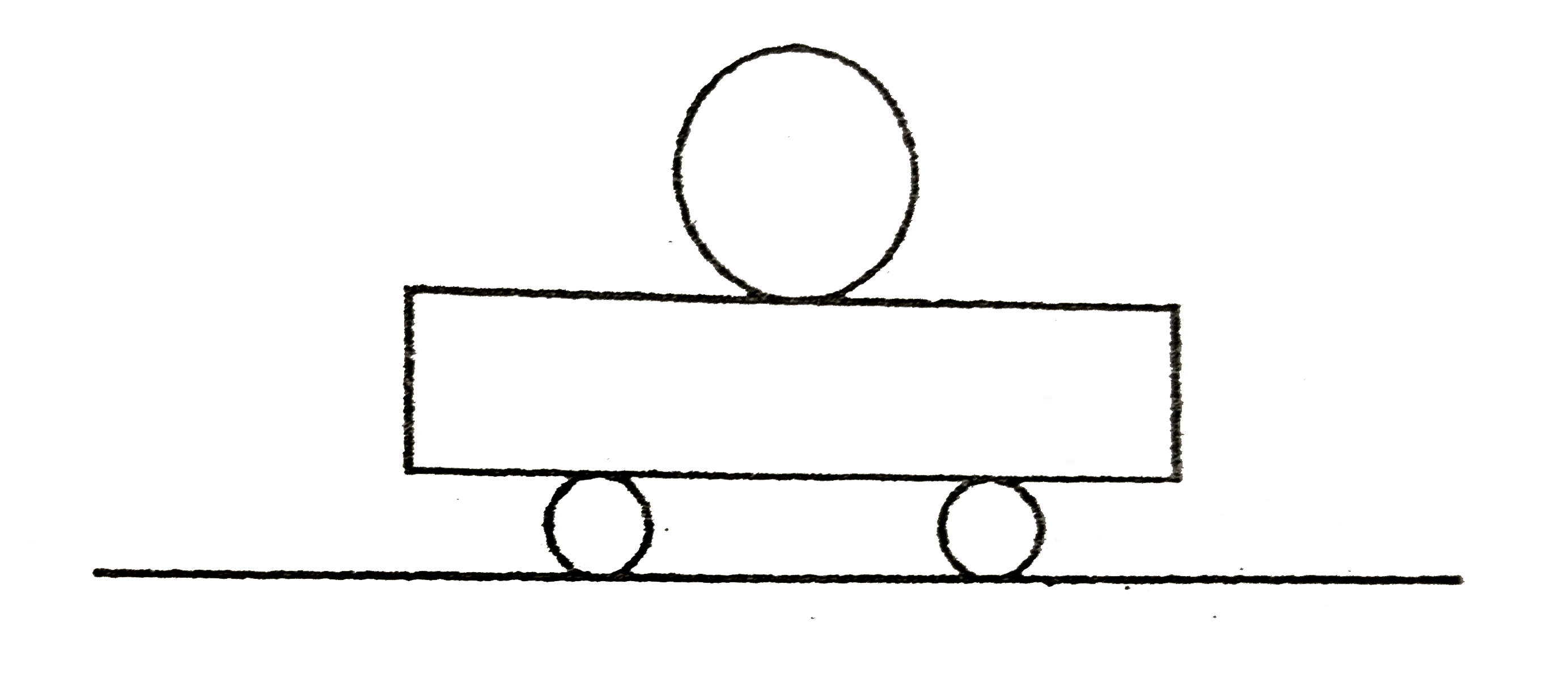
Acceleration of centre of mass of sphere is
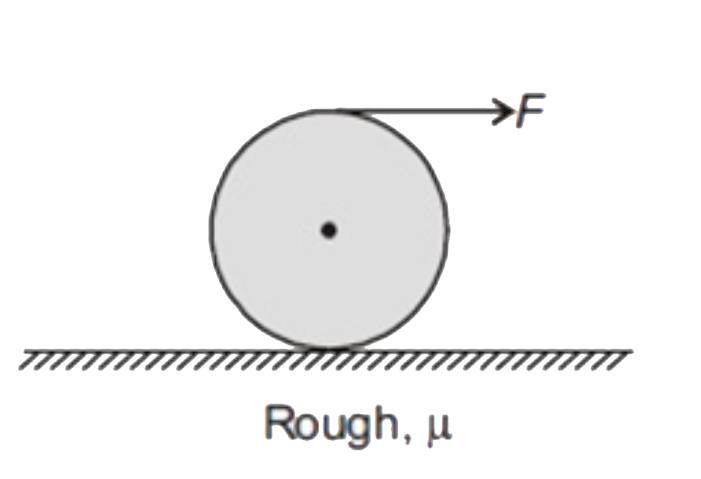
View SolutionA solid sphere of mass M and radius R is pulled by a force F as shown in figure . If the sphere does not slip over the surface , then frictional force acting on the sphere is
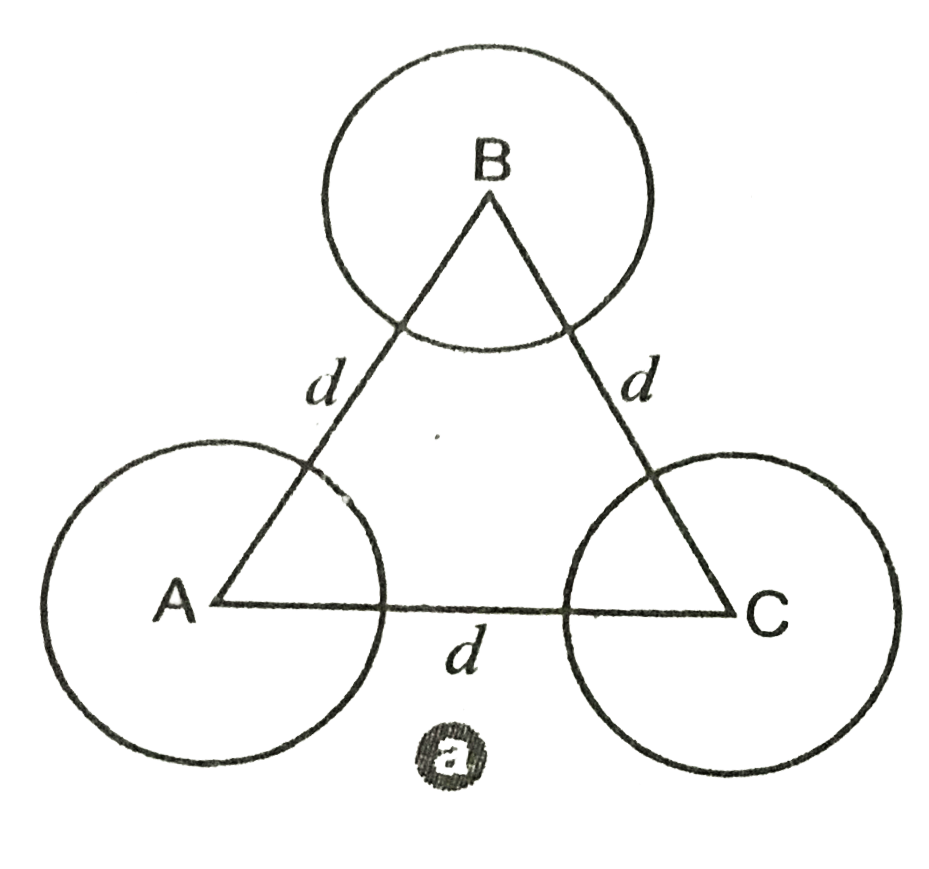
View SolutionThree solid spheres each of mass m and radius R are released from the position shown in Fig. What is the speed of any one sphere at the time of collision?
View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View SolutionA sphere of mass m held at a height 2R between a wedge of same m and a rigid wall, is released from, Assuming that all the surfaces are frictionless. Find the speed of the bodies when the sphere hits the ground.
 .
.
View Solution
