An insect of mass m is initially at one end of a stick of length L and mass M, which rests on a smooth floor. The coefficientg of friction between the insect and the stick is k. The minimum time in which the insect can reach the other end of the stick is t. Then t2 is equal to
2L/kg
2Lm/kg(M+m)
2LM/kg(M+m)
2Lm/kgM
The correct Answer is:C
An insect …………..
Maximum froce of friction =kmg
∴ maximum acceleration of insect =a1=kmgm=kg
and maximum acceleration of stick =a2=kmgM
∴ acceleration of insect with respect to stick
=a=a1−(−a2)=kg(1+mM)
∴L=12at2ort2=2La=2MLkg(M+m)
Similar Questions
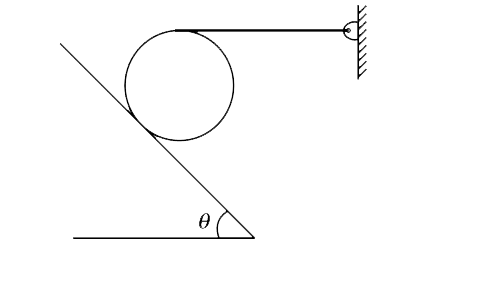
A horizontal stick of mass m has its right end attached to a pivot on a wall, while its left end rests on the top of a cylinder of mass m which in turn rests on an incline plane inclined at an angle θ. The stick remains horizontal. The coefficient of friction between the cylinder and both the plane and the stick is μ. Find the minimum value of μ as function of θ for which the system stays in equilibrium.
View SolutionWhen a stick of length L mass M intially upright on a fricitionless floor starts falling the
View Solution
Knowledge Check
A man of mass m walks from end A to the other end B of a boat of mass M and length l. The coefficient of friction between the man and the boat is μ an neglect any resistive force between the boat and the water.
AIf the man runs at his maximum acceleration, the acceleration of the boat is (m/M)μg.BThe minimum time take by the man to reach the other end of the boat is √2MI(M+m)μgCIf man runs at his maximum acceleration the acceleration of boat is mm+MμgDThe minimum time take by the man to reach the other end of the boat is √2ml(M+m)μgA bar of mass m1 is placed on a plank of mass m2 which rests on a smooth horizontal plane . The coefficient of friction between the surfaces of bar and plank is k . The plank is subjected to a horizontal force F depending on time t as F = at , where a is a constant . The moment of time t0 at which the plank starts sliding is :
 Aakgm1+m2B(m1+m2)kgaC(m1+m2)gkaDka(m1+m2)g
Aakgm1+m2B(m1+m2)kgaC(m1+m2)gkaDka(m1+m2)gA man of mass M stands at one end of a plank of length L which lies at rest on a frictionless surface. The man walks to the other end of the planck. If the mass of the planck is M2, then the distance that the man moves relative to the ground is
A3L4BL4C4L5DL3
A uniform stick of length l and mass m lies on a smooth table. It rotates with angular velocity ω about an axis perpendicular to the table and through one end of the stick. The angular momentum of the stick about the end is
View SolutionA boy of mass m is standing at one end of a boat of mass M and length l. The boy walks to the other end, the displacement of the
View SolutionA man of mass M stands at one end of a plank of length L Which lies at rest on a frictionless surface . The man walks to the other end of the plank. If the mass of the plank is 3M, the distance that the man moves relative to the ground is
View SolutionA man of mass M stands at one end of a stationary plank of length L, lying on a smooth surface. The man walks to the other end of the plank. If the mass of the plank is M/3, the distance that the man moves relative to the ground is
View SolutionA uniform rod of length l and mass 2m rests on a smooth horizontal table. A point of mass m moving horizontally at right angle to the rod with velocity v collides with one end of the rod and sticks to it, then:
View Solution