If tension in string A and string B are TA and TB then find out TATB (assume that stringe are light and g=10m/s2) :
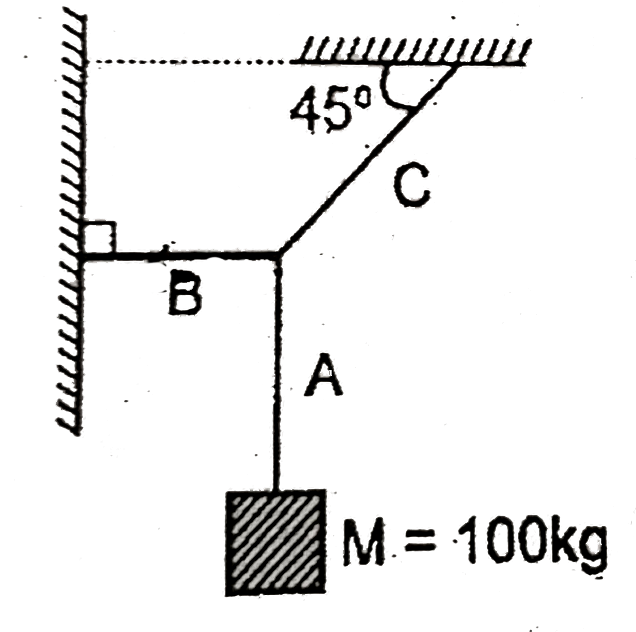
The correct Answer is:1
If tension …………
Tc√2=TA=TB
+
Similar Questions
Knowledge Check
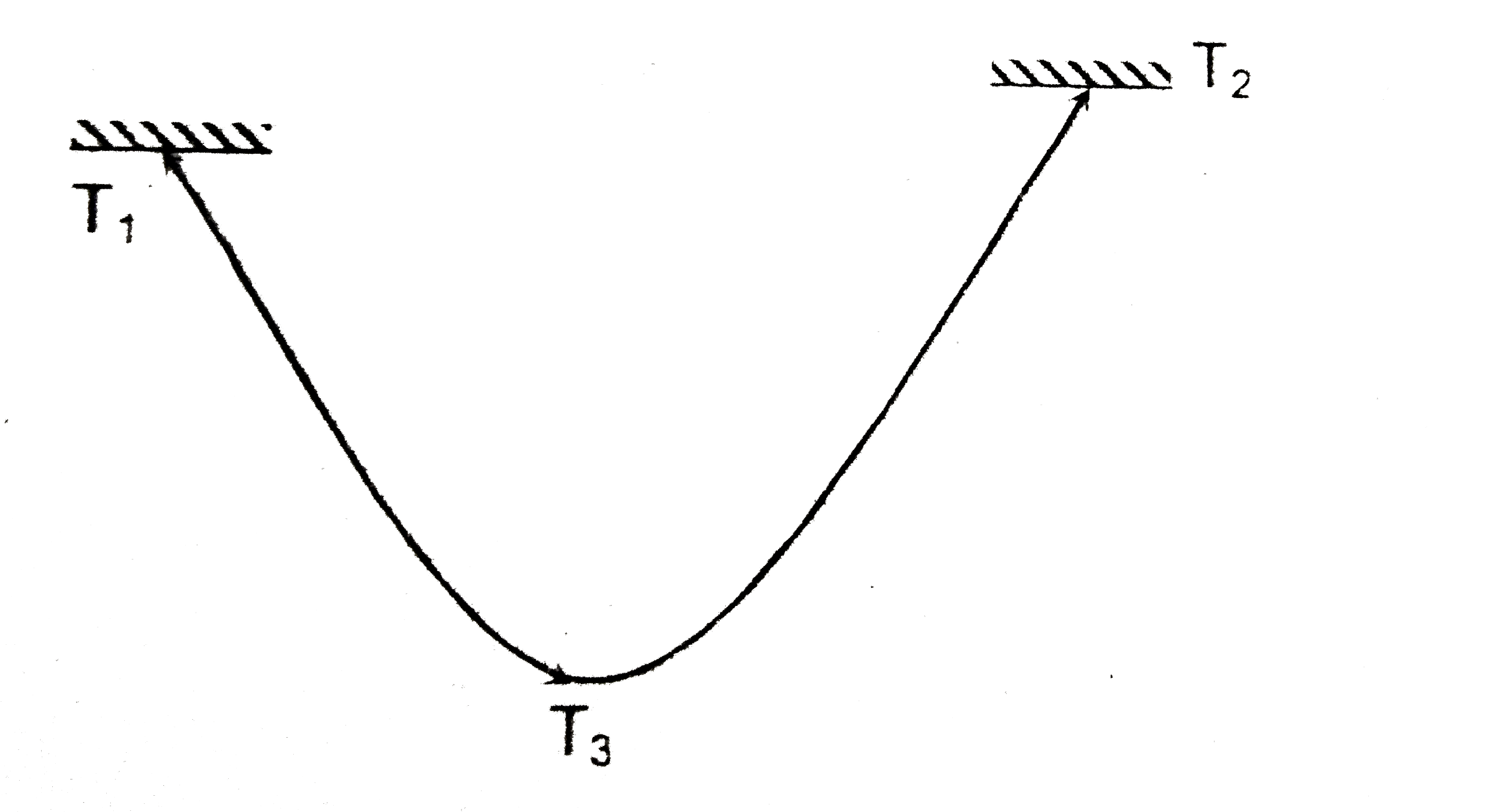 ltbrltgt A string of mass m (can be non uniform as well) is suspended through two points which are not in same horizontal level. Tension in the string at the end points are T1 and T2 and at the lowest point is T3. Mass of string in terms of T1,T2 and T3 can be represented a (uniform gravity 'g' exists downwards)A√T21−T23+√T22−T23gB(T1+T2−2T3)gC√T21+T22gD√T21+T23+√T22+T23g
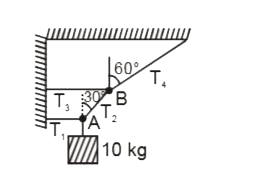
ltbrltgt A string of mass m (can be non uniform as well) is suspended through two points which are not in same horizontal level. Tension in the string at the end points are T1 and T2 and at the lowest point is T3. Mass of string in terms of T1,T2 and T3 can be represented a (uniform gravity 'g' exists downwards)A√T21−T23+√T22−T23gB(T1+T2−2T3)gC√T21+T22gD√T21+T23+√T22+T23gIn fig tension in the string that connects the masses A and B is T1 and that in the string connecting B and C is T2 then T1T2 is:
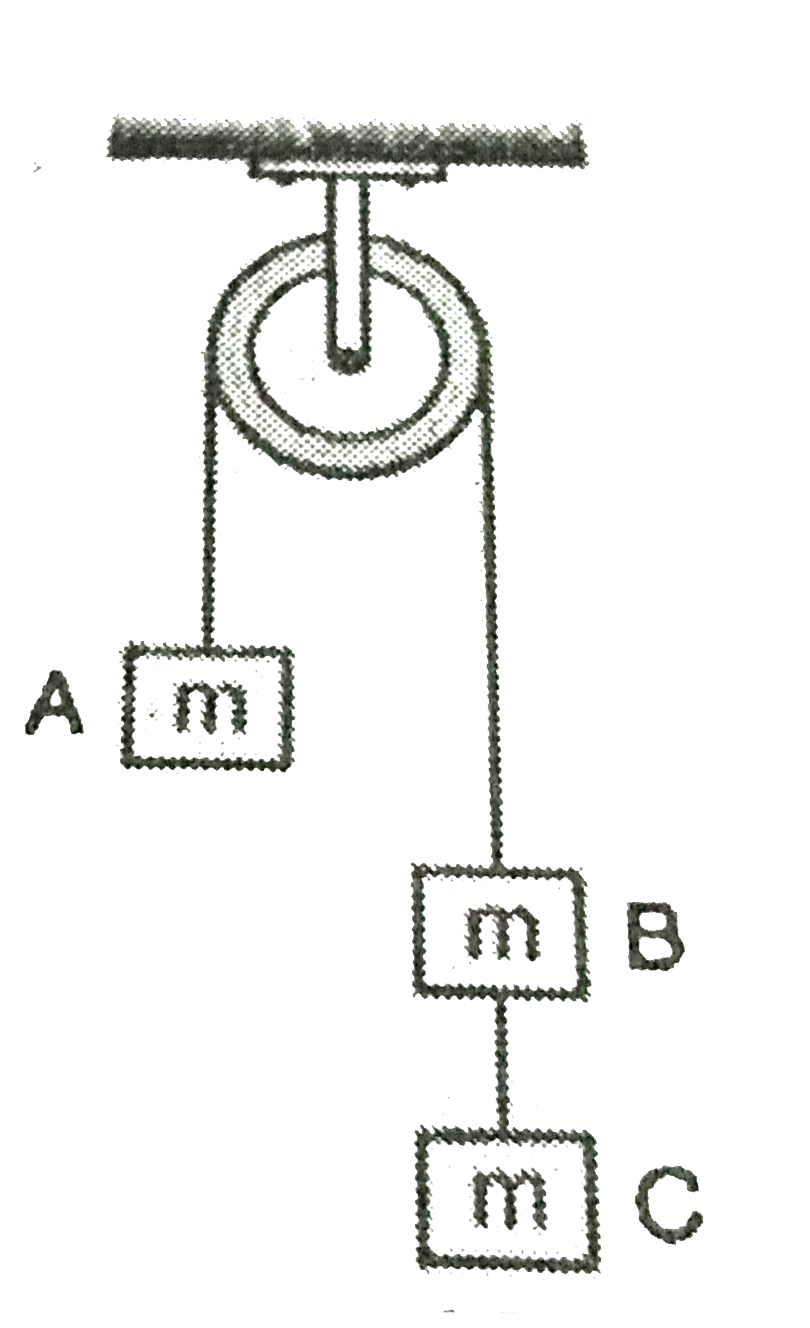 A2B0.5C4D0.25
A2B0.5C4D0.25A lift can move upward or downward. A light inextensible string fixed from ceiling of lift when a frictionless pulley and tensions in string T1. Two masses of m1andm2 are connected with inextensible light string and tension in this string T2 as shown in figure. Read the questionbs carefully and answer
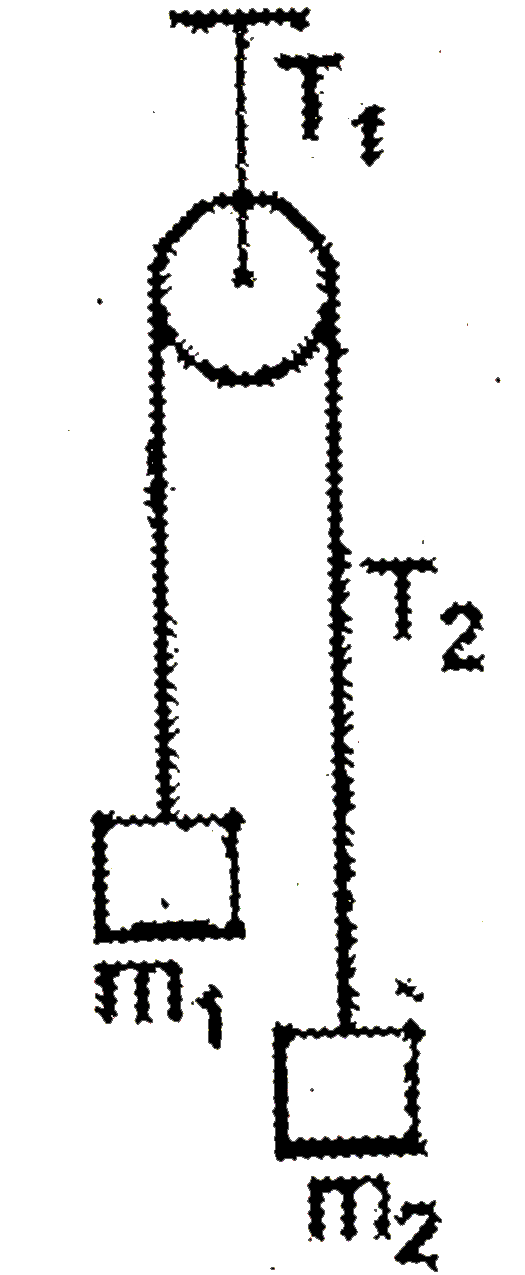
If m1+m2=m and lift is moving with constant velocity then value of T1 :A≥mgB=mgC≤mgD>mg
A particle of mass m is attached to a vertical rod with two inextensible strings AO and BO of equal lengths l. Distance between A and B is also l. The setup is rotated with angular speed ω with rod as the axis.
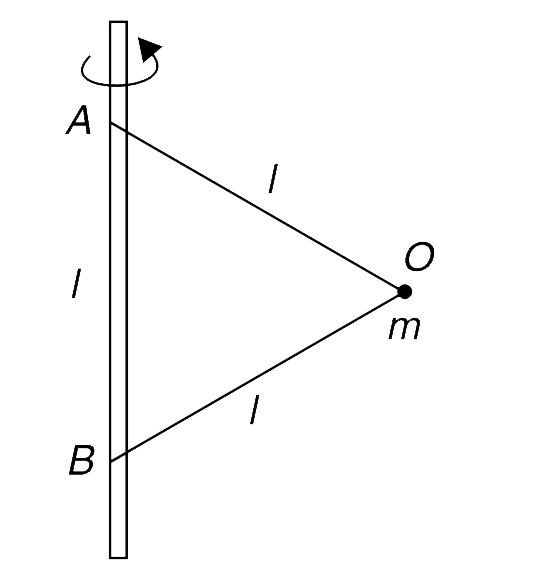
(a) Find the values of ω for which the particle remains at point B.
(b) Find the range of values of ω for which tension (T1) in the string AO is greater than mg but the other string remains slack
(c) Find the value of ω for which tension (T1) in string AO is twice the tension (T2) in string BO
(d) Assume that both strings are taut when the string AO breaks. What will be nature of path of the particle moment after AO breaks ?
View SolutionDetermine the tensions T1 and T2 in the string as shown in figure.
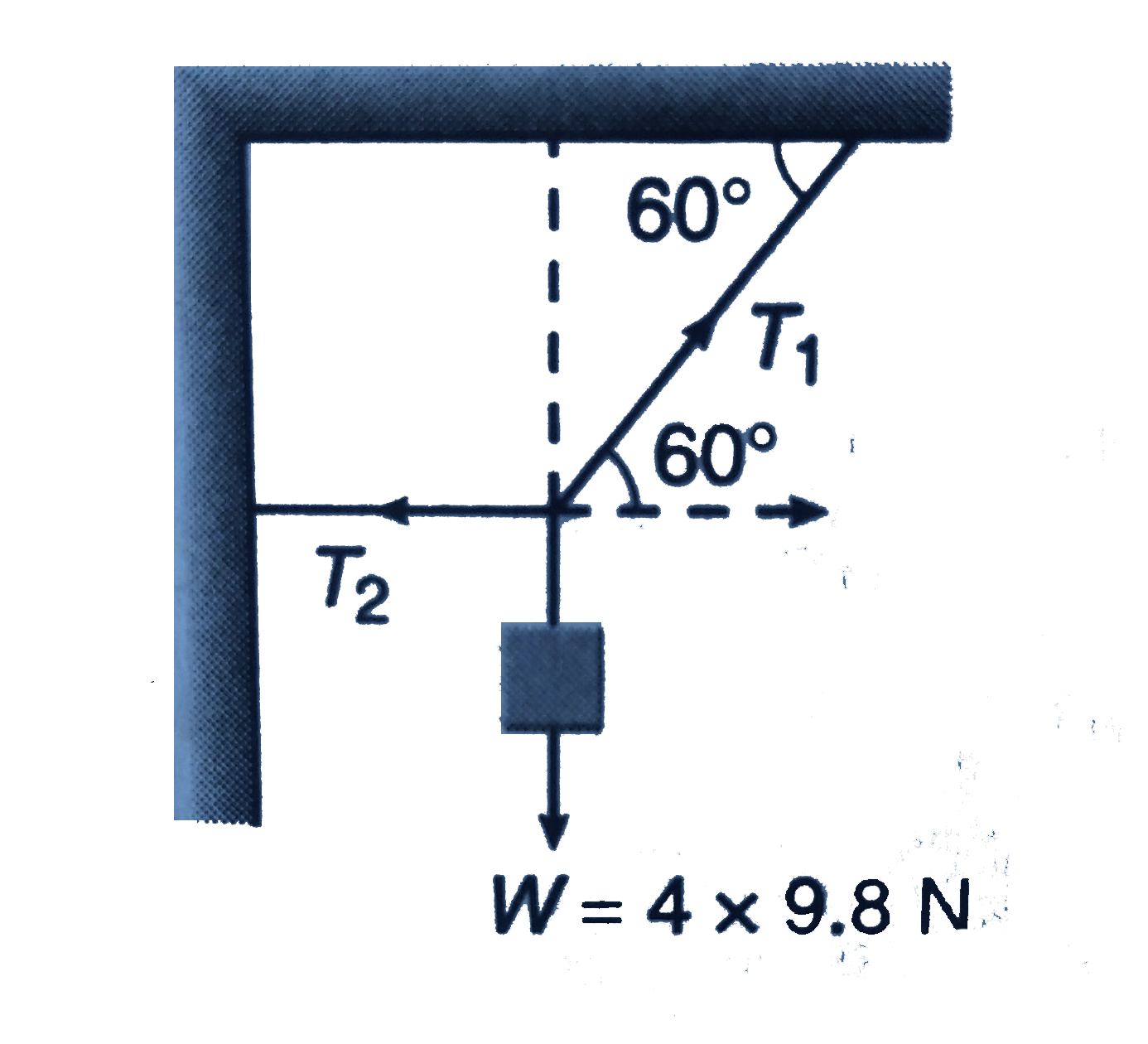
View SolutionThe system shown in figure is in equilibrium. Find the magnitude of tension in each string, T1,T2,T3 and T4(g=10m/s−2)
View SolutionA lift can move upward or downward. A light inextensible string fixed from ceiling of lift when a frictionless pulley and tensions in string T1. Two masses of m1andm2 are connected with inextensible light string and tension in this string T2 as shown in figure. Read the questionbs carefully and answer

If m1 is very small as compared to m2 and lift is moving with constant velocity then value of T2 is nearly :
View SolutionA lift can move upward or downward. A light inextensible string fixed from ceiling of lift when a frictionless pulley and tensions in string T1. Two masses of m1andm2 are connected with inextensible light string and tension in this string T2 as shown in figure. Read the questionbs carefully and answer
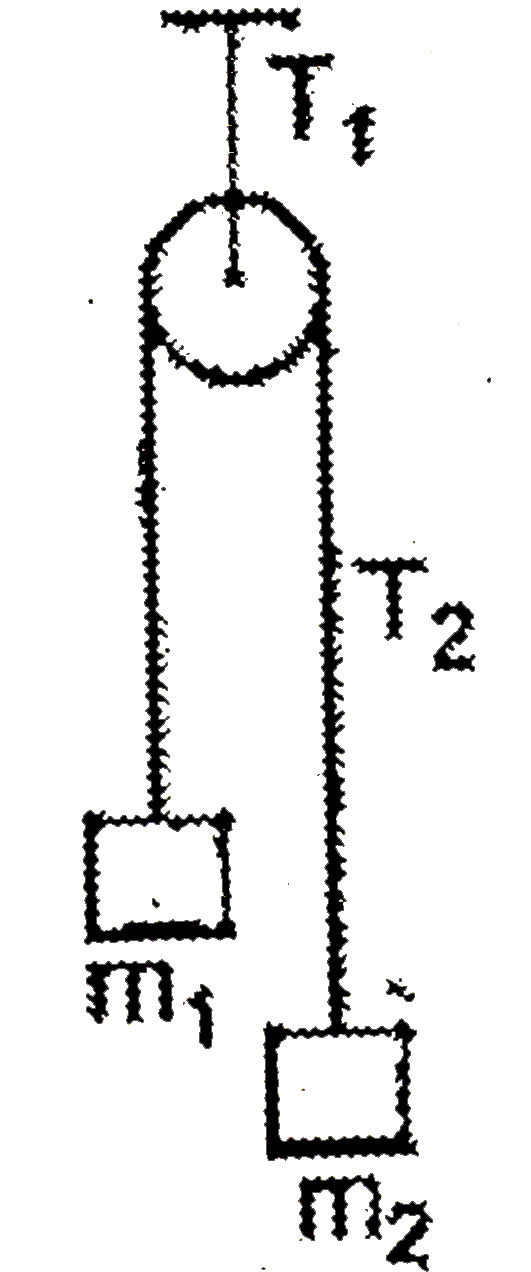
If m1=m2andm1 is moving at a certain instant with velocity v upward with respect to lift and the lift is moving in upward direction with constant acceleration (a<g) then speed of m1 with respect to lift :
View Solution



