Assume that a tunnel is dug across the earth (radius=R) passing through its centre. Find the time a particle takes to reach centre of earth if it is projected into the tunnel from surface of earth with speed needed for it to escape the gravitational field to earth.
The correct Answer is:t=sin−1(1√3)√Reg
let x= distance of the particle form the surface
acceleration
vdvdx=GMR3(R−x)
⇒vvevdv=∫x0g(1−xR)dx
⇒v=√v2e+2g(x−x22R)=dxdt
⇒∫t0dt=∫0Rdx√2g[R+x−x22R]
⇒t=∫0Rdx√gR[3R2−(x−R)2]
let x-R=√3Rsinθ
dx=√3Rcosθdθ
∴t=√Rg∫dθ=√Rgsin−1(x−R√3R)R0
⇒t=√Rgsin−1(1√3)
Topper's Solved these Questions
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:Exercise 5 A (Previous Year Questions)
Explore 26 Videos
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:Exercise 5 B (Previous Year Questions)
Explore 9 Videos
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:Exercise 4 A (Conceptual Subjective Exercise)
Explore 14 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:subjective
Explore 14 Videos
- KINEMATICS-2DBook:ALLENChapter:KINEMATICS-2DExercise:Exercise (O-2)
Explore 48 Videos
Similar Questions
Assume that a tunnel is dug across the earth (radius=R) passing through its centre. Find the time a particle takes to cover the length of the tunnel if (a) it is projected into the tunnel with a speed of √(gR) (b) it is relased from a height R above the tunnel (c ) it is thrown vertically upward along the length of tunnel with a speed of √gR.
View SolutionAssume that there is a tunnel in the shape of a circular arc through the earth. Wall of the tunnel is smooth. A ball of mass m is projected into the tunnel at A with speed v. The all comes out of the tunnel at B and escapes out of the gravity of the earth. Mass and radius of the earth are M and R respectively and radius of the circle shaped tunnel is also . Find minimum possible value of v (call it v0) If the ball is projected into the tunnel with speed v0, calculate the normal force applied by the tunnel wall on the ball when it is closest to the centre of the earth. It is given that the closest distance between the ball and the centre of the earth is R2

View Solution
Knowledge Check
A tunnel is made inside earth passing throgh centre of earth. A particle is dropped from the surface of earth. Select the correct statement :
 AKinetic energy of particle is maximum at centre and its potential energ is zero at centerBVelocity of particle is proportional to x [where x is distance of particle from center of earthCKinetic energy of particle is maximum when it reaches on the other side of tunnelDKinetic energy of particle is maximum at center
AKinetic energy of particle is maximum at centre and its potential energ is zero at centerBVelocity of particle is proportional to x [where x is distance of particle from center of earthCKinetic energy of particle is maximum when it reaches on the other side of tunnelDKinetic energy of particle is maximum at centerA hole is drilled along the diameter of the earth and pen is dropped into it. The time taken by it is reach other end of the earth is
A162.2 minB84.6 minC21.2 minD42.3 minIf g is the acceleration due to gravity at the earth's surface and r is the radius of the earth, the escape velocity for the body to escape out of earth's gravitational field is
AgrB√2grCg/rDr/g
Assume that a frictionless tunnel is made in the earth along its diameter, a particle in projected in the tunnel from the surface of the earth with an initial speed v0=√gR, where g is the acceleration due to gravity on the earth's surface & R is the radius of the earth, if time taken by the particle to reach the centre of the earth is πn√4Rg the value of n is?
View SolutionA ball of mass m is dropped from a height h in a tunnel, made across the earth (mass = M, radius = R) passing through its center. If h<<R such that the motion of the particle through h can be considered uniformly accelerated at g, then the time period of the particle is
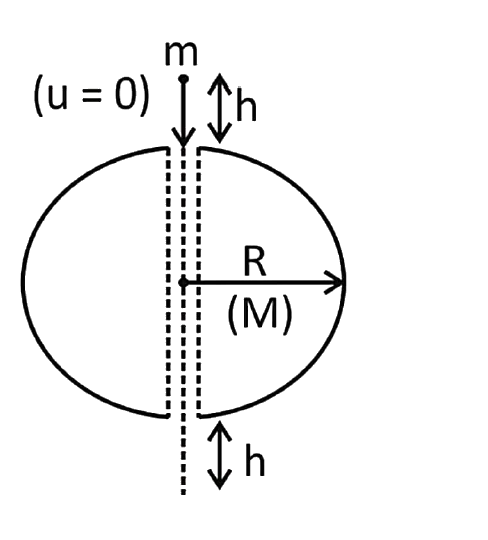
View SolutionA hole is drilled from the surface of earth to its centre. A particle is dropped from rest in the surface of earth in terms of its escape velocity on the surface of earth ve is :
View SolutionIn the above question, escape speed from the centre of earth is :
View SolutionA tunnel has been dug through the centre of the earth and a ball is released in it. It will reach the other end of the tunnel after
View Solution
