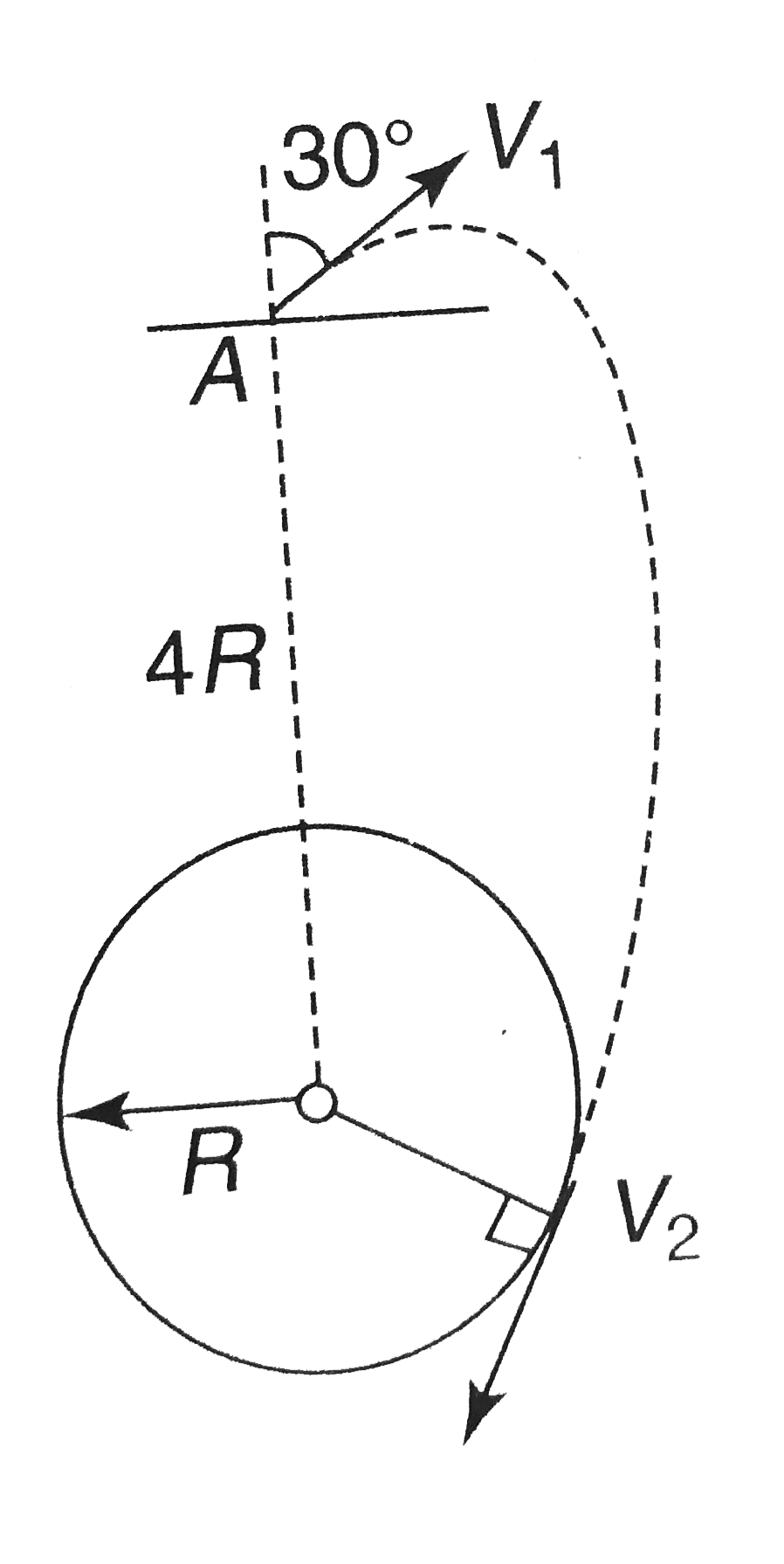
A particle is projected from point A, that is at a distance 4R form the centre of the earth, with speed V1 in a direction making 30∘ with the line joining the centre of the earth and point A, as shown. Consider gravitational interaction only between thesetwo. (Use GMR=6.4×107m2/s2). The speed V1 if particle pasess grazing the surface of the earth is
8000√2
800
800√2
None of these
The correct Answer is:A
Conserving angular momentum :m(v1cos60∘)4R=mv2R⇒v2v1=2
Conserving energy of the system :GMm4R+12mv21=GMmR+12mv22
⇒12v22−12v21=34GMR⇒v21=12GMR⇒v1=1√2√64×106=8000√2m/s
Topper's Solved these Questions
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:Exercise 1 (Check your Grasp)
Explore 28 Videos
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:Exercise 2 (Brain Teasers)
Explore 27 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:subjective
Explore 14 Videos
- KINEMATICS-2DBook:ALLENChapter:KINEMATICS-2DExercise:Exercise (O-2)
Explore 48 Videos
Similar Questions
A particle is projected from point A, which is at a distance 4R from the centre of the earth, with speed v1 in a direction making 30∘ with the line joining the centre of the earth and point A, as shown. Find the speed v1 if particle passes grazing the surface of the earth. Consider gravitational interaction only between these two. Express you answer in the form 1000X√2~ms and find value of X. (Use GMR= 6.4×107m2s2 )
'(##CEN_KSR_PHY_JEE_C10_033_Q03##)'
View SolutionAn asteroid was fast approaching the earth. Scientists fired a rocket which hit the asteroid at a distance of 5 R from the centre of the earth (R = radius of the earth). mmediately after the hit the asteroid’s velocity (V0) was making an angle of θ=30∘ with the line joining the centre of the earth to the asteroid. The asteroid just grazed past the surface of the earth. Find V0 [Mass of the earth = M]

View Solution
Knowledge Check
A body at rest starts from a point at a distance r (gtR) from the centre of the Earth. If M and R stand for the speed of the body when it reaches the Earth surface is
A√2GMRB√2GMR−rC√2GM(r−R)RrDZeroA particle is projected vertically with speed V from the surface of the earth . Maximum height attained by the particle , in term of the radius of earth R,V and g is ( V < escape velocity , g is the acceleration due to gravity on the surface of the earth )
A3RV22gR−2V2B2RV23gR−V2CRV22gR−V2DRV2gR−2V2If d is the distance between the centre of the earth of mass M1 and the moon of mass M2, then the velocity with which a body should be projected from the mid point of the line joining the earth and the moon, so that it just escape is
A√G(M1+M2)dB√G(M1+M2)2dC√2G(M1+M2)dD√4G(M1+M2)d
The distance between earth and moon is d and the mass of earth is 81 times that of the moon. If the location of. neutral point from the centre of the earth on the line joining the centres of the earth and moon is nd10, then find n.
View SolutionTwo satellites S1 and S2 revolve around the earth at distances 3R and 6R from the centre of the earth. Find the ratio of their (a) linear speeds and (b) angular speeds.
View SolutionThe gravitational field intensity at a point 10 × 103 km from the centre of the earth is 4.8 N kg−1 . The gravitational potential at that point is
View SolutionA satellite S1 of mass m is revolving at a distance of R from centre of earth and the other satellite S2 of mass 4m is revolving at a distance of 4R from the centre of earth. The time periods of revolution of two satellites are in the raito 1 : n. Find the value of n.
View SolutionThe gravitational field intensity at a point 10,000km from the centre of the earth is 4.8Nkg−1. The gravitational potential at that point is
View Solution