Two spheres P and Q of equal radii have densities ρ1 and ρ2, respectively. The spheres are connected by a massless string and placed in liquids L1 and L2 of densities σ1 and σ2 and viscosities η1 and η2, respectively. They float in equilibrium with the sphere P in L1 and sphere Q in L2 and the string being taut(see figure). If sphere P alone in L2 has terminal velocity →Vp and Q alone in L1 has terminal velocity →VQ, then
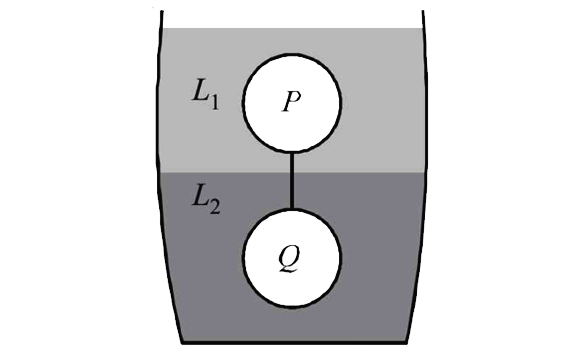
∣∣→VP∣∣∣∣→VQ∣∣=η1η2
∣∣→VP∣∣∣∣→VQ∣∣=η2η1
→VP.→VQ>0
→VP.→VPQ<0
The correct Answer is:A, D
Step by step video, text & image solution for Two spheres P and Q of equal radii have densities rho_1 and rho_2, respectively. The spheres are connected by a massless string and placed in liquids L_1 and L_2 of densities sigma_1 and sigma_2 and viscosities eta_1 and eta_2, respectively. They float in equilibrium with the sphere P in L_1 and sphere Q in L_2 and the string being taut(see figure). If sphere P alone in L_2 has terminal velocity vecV_p and Q alone in L_1 has terminal velocity vecV_Q, then by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Comprehension)5videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Assertion Reason)1videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (MCQ)13videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B19videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)22videos
ERROR AND MEASUREMENT
Similar Questions
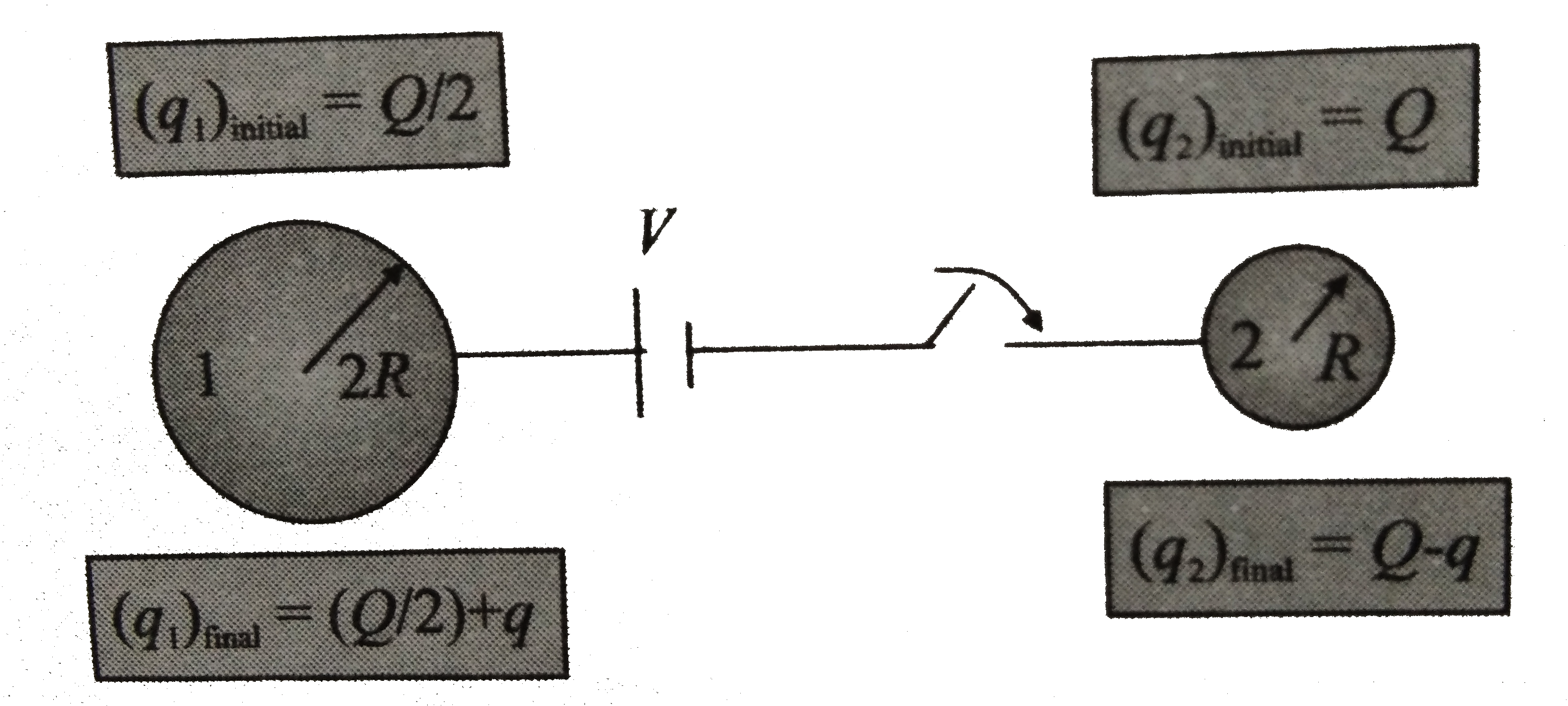
There are two spheres of radii R and 2R having charges Q and Q/2, respectively. These two spheres are connected with a cell of emf V volts as show in. When the switch is closed, find the final charge on each sphere.
 View Solution
View SolutionConsider two solid spheres P and Q each of density 8gmcm−3 and diameters 1cm and 0.5cm, respectively. Sphere P is dropped into a liquid of density 0.8gmcm−3 and viscosity η=3 poiseulles. Sphere Q is dropped into a liquid of density 1.6gmcm−3 and viscosity η=2 poiseulles. The ratio of the terminal velocities of P and Q is
View Solution
Knowledge Check
- Question 1 - Select One or More
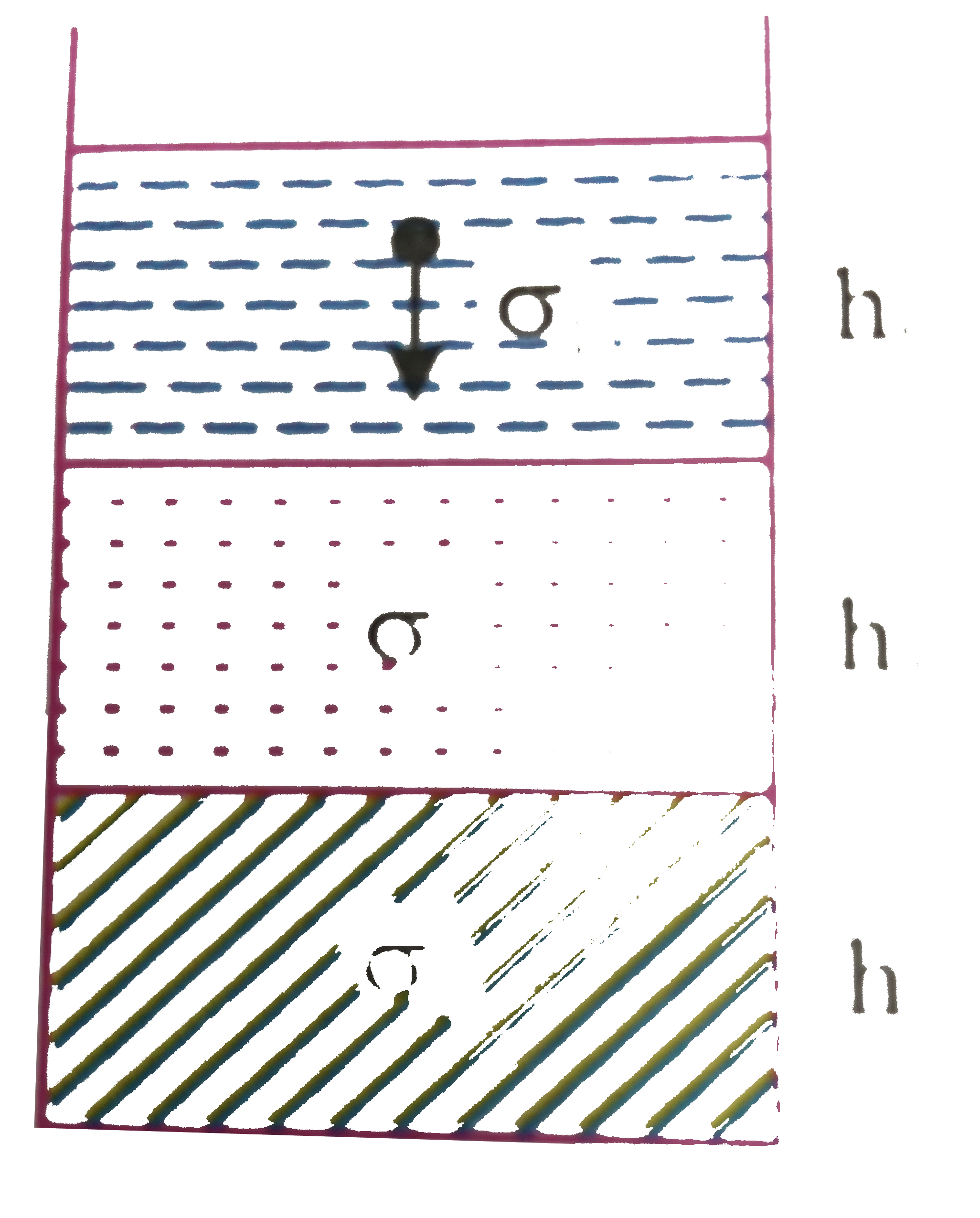
A ball moves successively through three liquids, at rest as shown, of densities σ1,σ2 and σ3 and viscosity coefficient η1,η2 and η3 and respectively with the same terminal velocity thenAη3>η2>η1Bσ1η1=σ2η2=σ3η3Cη1η3>η3η2Dη2σ1−η1σ2η3σ1−η1σ3=η2−η1η3−η1 - Question 2 - Select One
Two conducting spheres of radii r1 and r2 having charges Q1 and Q2 respectively are connected to each other. There is
Ano change in the energy of the systemBan increase in the energy of the systemCalways a decrease in the energy of the systemDa decrease in the energy of the system unless Q1r2=Q2r1 - Question 3 - Select One
Two wires of equal diameters, of resistivities ρ1 and ρ2 and length l1 and l2, respectively of the combination is
Aρ1l1+ρ2l2l1+l2Bρ1l2+ρ2l1l1−l2Cρ1l2+ρ2l1l1+l2Dρ1l1+ρ2l2l1−l2
The insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
View SolutionTwo wires of same radius having lengths l1, and l2 and resistivities ρ1 and ρ2 are connected in series. The equivalent resistivity will be
View SolutionThe insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
View SolutionTwo wires of equal diameters of resistivies ρ1 and ρ2 and lengths l and l respectively are joined in series. The equivalent resistivity of the combination is
View SolutionTwo spherical conductors of radii R1andR2 are separated by a distance much larger than the radius of eighter sphere. The spheres are connected by a conducting wire as shown in (Fig. 3.128). If the charges on the spheres in equilibrium are q1andq2, respectively, what is the ratio of the field strength at the surfaces of the spheres ?
 .View Solution
.View Solution
