The focal length of convex tens is f and the distance of an object from the principal focus is x. The ratio of the size of the real image to the size of the object is
fx
xf
f+xf
ff+x
The correct Answer is:A
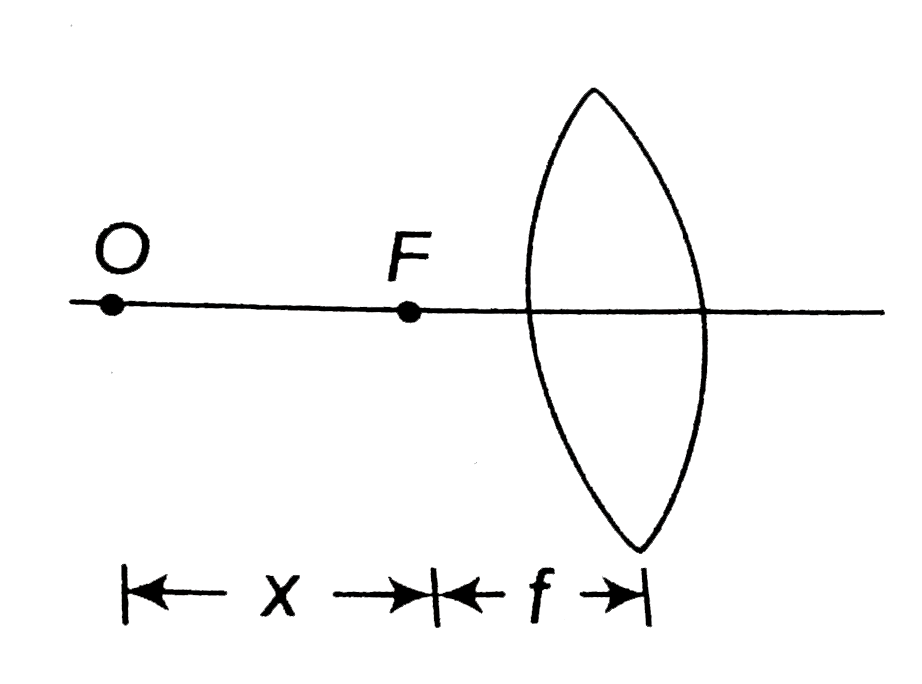
1v−1−(f+x)=1f
1v=1f−1f+x=xf(f+x)⇒vf(f+x)x
IO=vu=f(f+x)−x(f+x)=−fx
Related Playlists
- BOOK - CP SINGHCHAPTER - REFRACTION AT SPHERICAL SURFACESEXERCISE - EXERCISES105videos
REFRACTION AT SPHERICAL SURFACES
- BOOK - CP SINGHCHAPTER - REFLECTION OF LIGHTEXERCISE - EXERCISES67videos
REFLECTION OF LIGHT
- BOOK - CP SINGHCHAPTER - REFRACTION OF LIGHT BY PLANE SURFACESEXERCISE - Exercises110videos
REFRACTION OF LIGHT BY PLANE SURFACES
Similar Questions
What is the distance of an object from a concave mirror of focal length 20 cm so that the size of the real image is three times the size of the object ?
View SolutionAssertion : The focal length of the mirror is f and distance of the object from the focus is u , the magnification of the mirror is f/u.
Reason : Magnification =Size of the imageSize of objectView SolutionFind the distance of object from a concave mirror of focal length 10 cm so that image size is four time the size of the object.
View SolutionDraw a labelled ray diagram for the formation of image by a convex lens of focal length 15 cm when the object is placed at a distance of 25 cm from the lens. Determine the size of the image formed, if size of the object is 4 cm.
View SolutionFind the distance of object form a concave morror of focal length 10 cm so that image size is four times the size of the object.
View SolutionAn object is placed …………. Of a convex lens to get a real image with the size of the object.
View SolutionThe focal length of convex lens is 30 cm and the size of image is quarter of the object, then the object distance is
View SolutionCalculate two possible distances of an object from a convex lens of focal length 20 cm so as to obtain an image of double the size of the object.
View SolutionWhat distance should an object be placed in front of a convex lens of focal length 0.4 m so that the image is thrice the size of the object ?
View SolutionAt what distance should an object be placed from a convex lens of focal langth 15cm to obtain an image three times the size of the object ?
View Solution


