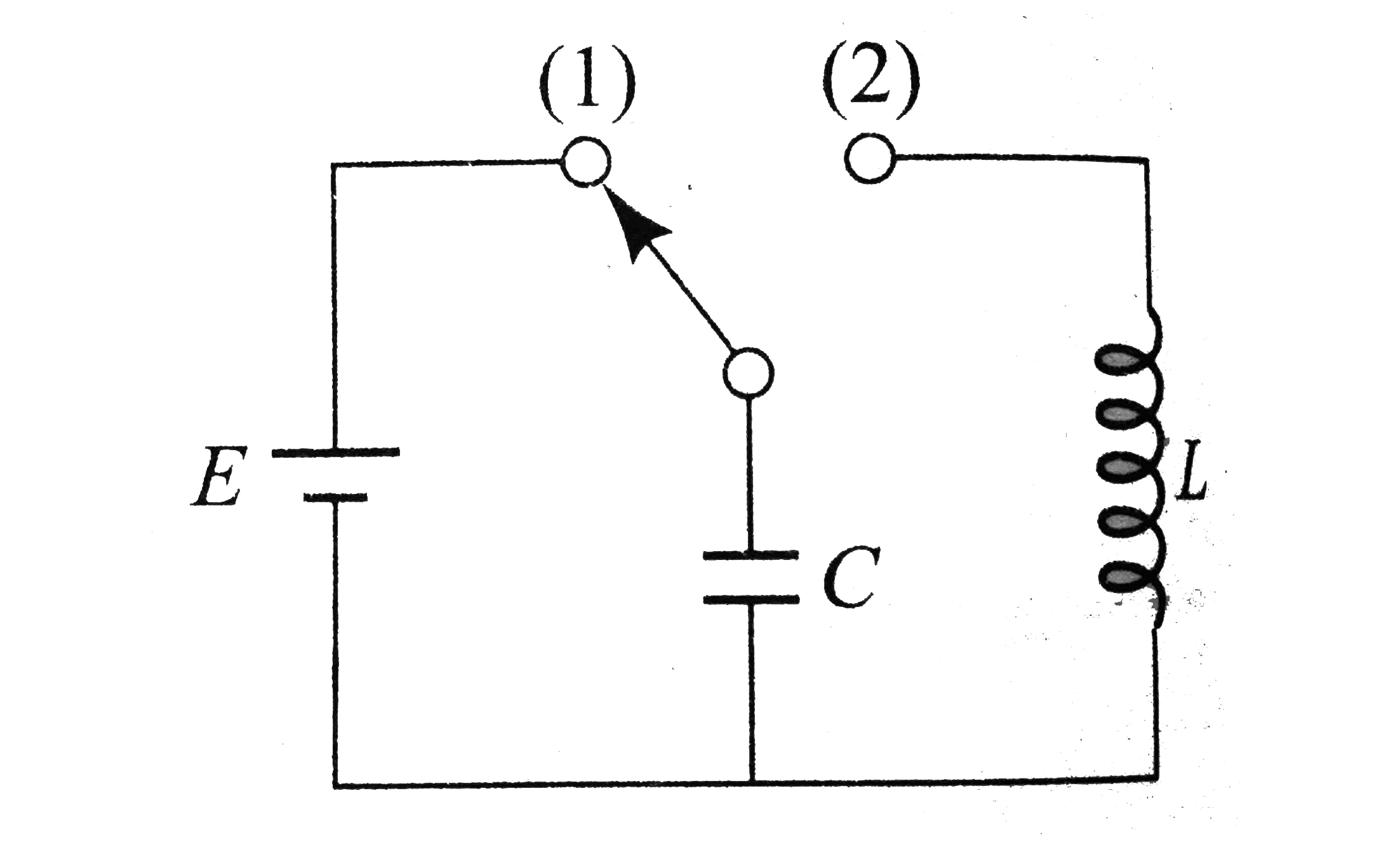
In the following electrical network at t<0, key is placed on (1) till the capacitor got fully charged. Key is placed on (2) at t=0. Time when the energy in both the capacitor and inductor will be same for the first time is
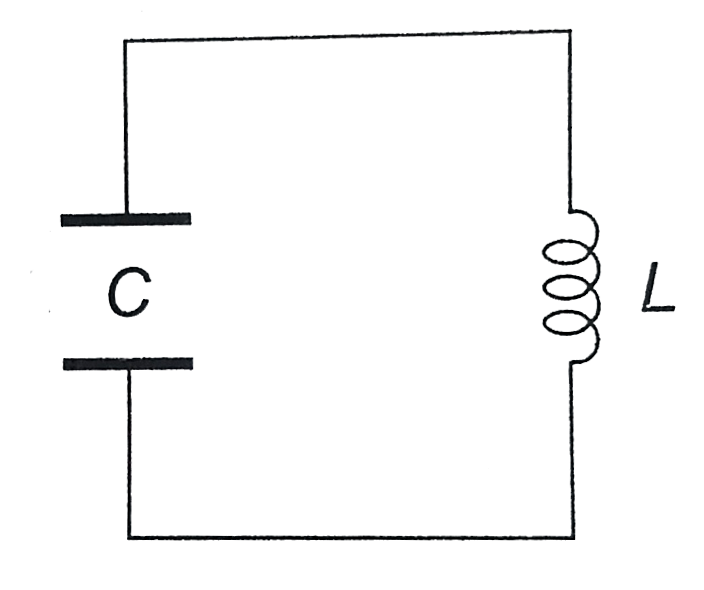
At t=0 , change on capacitor q0=CE
Change on capacitor in terms of t
q=q0cosωt , ω=1√LC
UL+UC=q202C
UL=UC
2UC=q202C implies UC=q204C implies q22C=q204C
q=(q0)'√2
q=q0cosωt
q0√2=q0cosωt implies cosωt=1√2=cos(π)4
ωt=π4 implies t=π4ω=π4√LC
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the following electrical network at t=<0 Fig key is placed on (1) till the capacitor got fully charged. Key is placed on (2) at t=0. Time when the energy in both the same for the time is
 Aπ4√LCB3π4√LCCπ3√LCD2π3√LC
Aπ4√LCB3π4√LCCπ3√LCD2π3√LCIn the circuit shown key is closed at t=0 with capacitor initially uncharged.
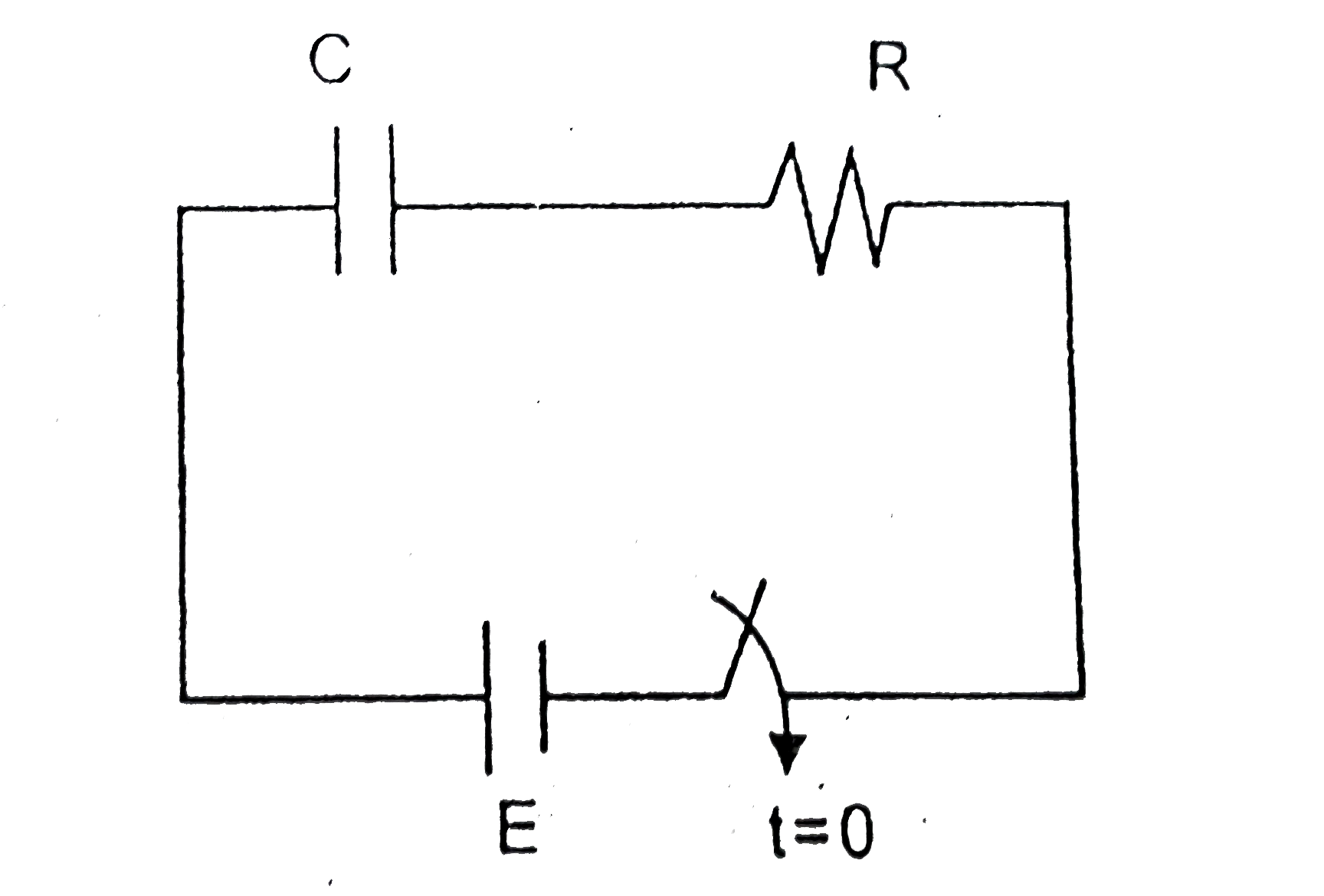 ARate of increase of capacitors energy, just after the switch is closed is E2RBMaximum power supplied by the cell is E2RCAt t=RCIn2, capacitor is charged up to half of the energy stored by it in steady stateDAt t=RCIn2, potential difference across capacitor is same that across resistor.
ARate of increase of capacitors energy, just after the switch is closed is E2RBMaximum power supplied by the cell is E2RCAt t=RCIn2, capacitor is charged up to half of the energy stored by it in steady stateDAt t=RCIn2, potential difference across capacitor is same that across resistor.The circuit is completed at t=0, then heat loss in R=4Ω resistance, till the capacitor gets fully charged.
 A64μJB384μJC320μJD576μJ
A64μJB384μJC320μJD576μJ
An Uncharged capacitor C is connected to a battery through a resistance R. Show that by the time the capacitor gets fully charged, the energy dissipated in R is the same as the energy stored in C.
View SolutionA circuit contains 50 μF capacitor and 20 mH inductor connected together with the help of a key which is open initially. Charge stored in the capacitor is 50 mC. Key is closed at t=0 . Calculate the minimum time interval in which energy stored in the inductor becomes equal to the energy stored in capacitor . Neglect any resistance in the circuit .
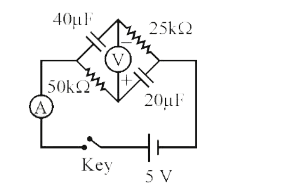
View SolutionIn the circuit shown below, the key is pressed at time t = 0. The correct statement is
View SolutionIn the given at t=0, switch S is closed.
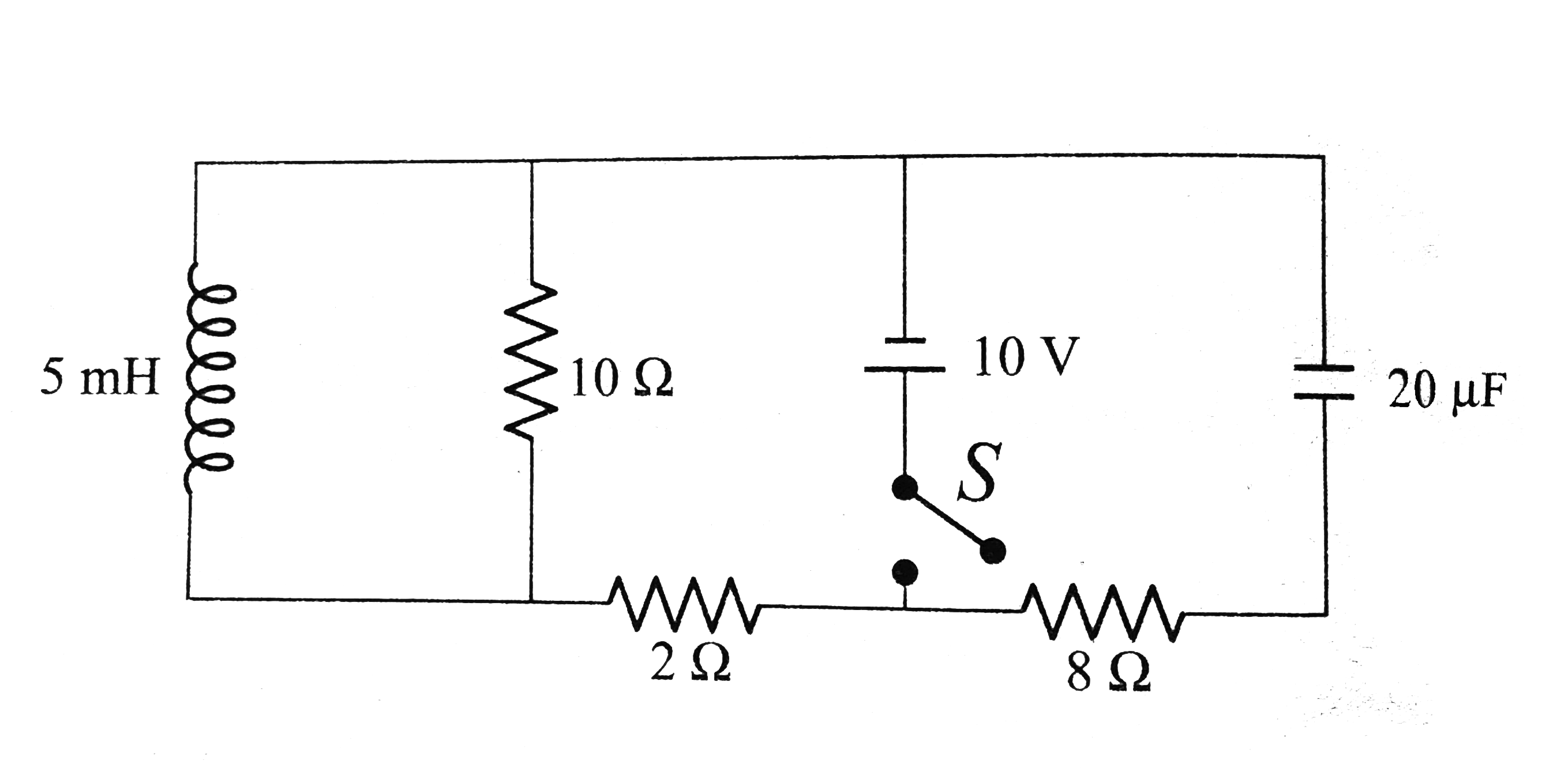
The energy stored in the capacitor and inductor, respectively, at t→∞ will be
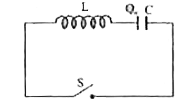
View SolutionAt t<0, the capacitor is charged and the switch is opened.At t=0 the switch is closed.The shortest time T at which the charge on the capacitor will be zero is given by:
View Solution