A small circular loop of radius a is placed inside a large square loop of edge L(>>a) . The loops are coplanar and concentric. Find mutual inductance.
To find the mutual inductance between a small circular loop of radius a and a large square loop of edge L (where L>a), we can follow these steps:
Step 1: Understand the Configuration
We have a small circular loop of radius a placed inside a large square loop with edge length L. Both loops are coplanar and concentric.
Step 2: Determine the Magnetic Field Due to the Square Loop
The magnetic field B at the center of the square loop due to the current I flowing through it can be calculated. The magnetic field at the center of a square loop can be derived using the formula:
B=μ0I4πD⋅(sinα+sinβ)
Where:
- D is the distance from the center to the side of the square loop.
- α and β are the angles subtended by the sides of the square at the center.
For a square loop, D=L2 and both angles α and β are 45∘.
Step 3: Calculate the Magnetic Field
Using sin45∘=1√2:
B=μ0I4π⋅L2⋅(2⋅sin45∘)=μ0I2πL⋅√2
Thus, the magnetic field at the center of the square loop is:
B=μ0I√22πL
Step 4: Calculate the Total Magnetic Field
Since the square loop has four sides contributing equally to the magnetic field at the center, the total magnetic field Bnet is:
Bnet=4⋅μ0I√22πL=2μ0I√2πL
Step 5: Calculate the Magnetic Flux Through the Circular Loop
The magnetic flux Φ through the circular loop is given by:
Φ=Bnet⋅A
Where A is the area of the circular loop:
A=πa2
Thus, the total flux is:
Φ=2μ0I√2πL⋅πa2=2μ0I√2a2L
Step 6: Relate Flux to Mutual Inductance
The mutual inductance M is defined as:
Φ=M⋅I
From this, we can express M:
M=ΦI=2μ0√2a2L
Final Result
Thus, the mutual inductance M between the small circular loop and the large square loop is:
M=2√2μ0a2L
We have a small circular loop of radius a placed inside a large square loop with edge length L. Both loops are coplanar and concentric.
The magnetic field B at the center of the square loop due to the current I flowing through it can be calculated. The magnetic field at the center of a square loop can be derived using the formula:
- D is the distance from the center to the side of the square loop.
- α and β are the angles subtended by the sides of the square at the center.
Using sin45∘=1√2:
Since the square loop has four sides contributing equally to the magnetic field at the center, the total magnetic field Bnet is:
The magnetic flux Φ through the circular loop is given by:
The mutual inductance M is defined as:
Thus, the mutual inductance M between the small circular loop and the large square loop is:
Topper's Solved these Questions
Similar Questions
A small square loop of wire of side l is placed inside a large squre loop of wire of side L(>>l). The loops are coplanar and their centre coincide. What is the mutual inductance of the system ?
View SolutionA small square loop of wire of side l is placed inside a large square loop of wire of side (L>>l). The loops are coplanar and their centres coincide. If the mutual inductance of the system is p√qμ0πl2L, then find (p+q).
View Solution
Knowledge Check
A small square loop of wire of side l is placed inside a large square loop of wire of side L(L>>l). The loops are co-planer and their centres coincide. The mutual inductance of the system is proportional to
AlLBl2LCLlDL2lA very small circular loop of radius a is initially coplanar & concentric with a much larger circular loop of radius b (>>a). A constant current is passed in the large loop which is kept fixed in space & the small loop is rotated with angular velocity omega about a diameter. The resistance of the small loop is R & its self inductance is negligible. The current in the larger loop is clockwise.
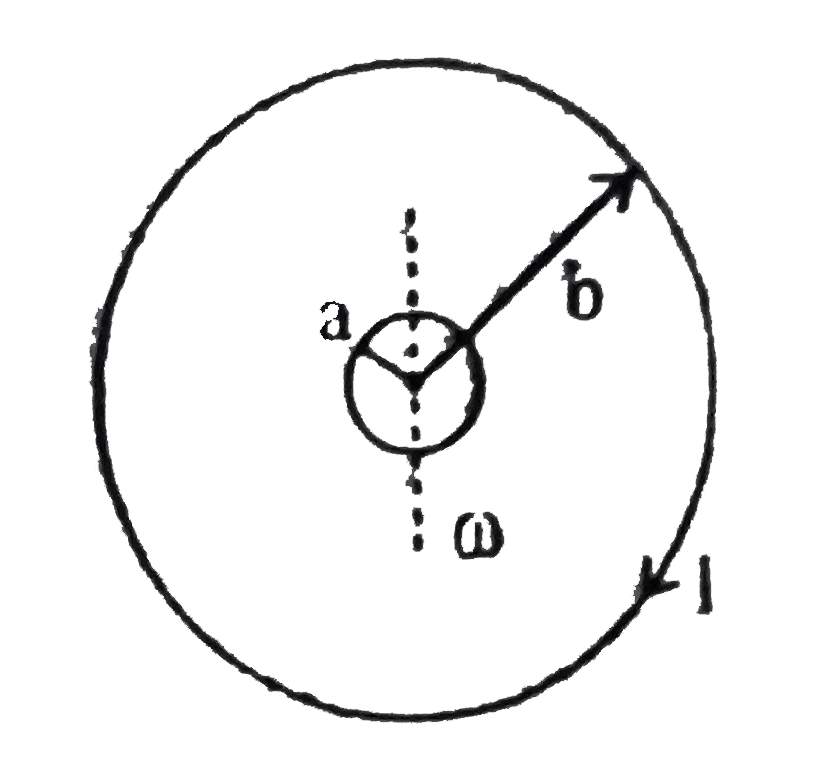
Find the current in the small loop as a function of time.Aπa2μ0Iωsinωt2bRBπa2μ0Iωcosωt2bRCπb2μ0Iωsinωt2aRDπb2μ0Iωcosωt2aRA very small circular loop of radius a is initially coplanar & concentric with a much larger circular loop of radius b (>>a). A constant current is passed in the large loop which is kept fixed in space & the small loop is rotated with angular velocity omega about a diameter. The resistance of the small loop is R & its self inductance is negligible. The current in the larger loop is clockwise.
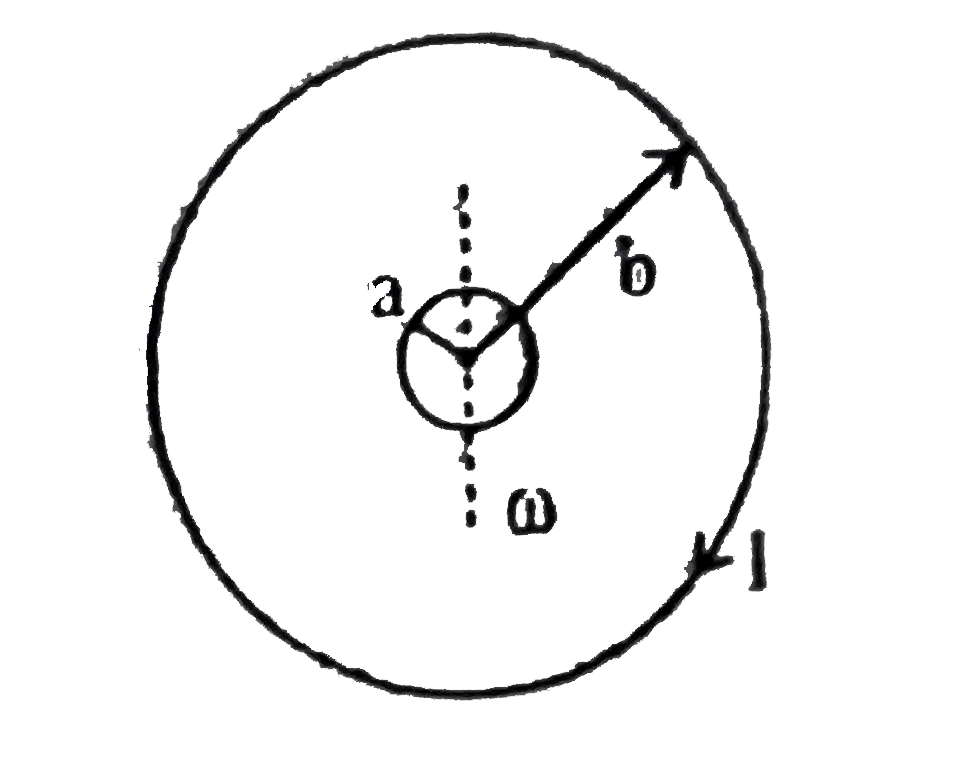
Calculate how much torque must be exerted on the small loop to rotate it.AωR(πb2μ0Isinωt2b)2BωR(πb2μ0I2b)2sinωtcosωtCωR(πa2μ0Isinωt2b)2DNone of these
A small square loop of wire of side l is placed inside a large square loop of wire of side L(L>>l) .The loops are coplanar and their centers coincide.The mutual inductance of the system is proportional to
View SolutionA small square loop of wire of side I is placed inside a large square loop of wire of side L(L>> ) .The loops are coplanar and their centers coincide.The mutual inductance of the system is proportional to
View SolutionA small square loop of wire of side I is placed inside a large square loop of wire of side L(L>> I ) .The loops are coplanar and their centers coincide. The mutual inductance of the system is proportional to
View SolutionA small square loop of side 'a' and one turn is placed inside a larger square loop of side b and one turn (b>>a). The two loops are coplanar with their centres coinciding. If a current I is passed in the square loop of side 'b', then the coefficient of mutual inductance between the two loops is :
View SolutionA circular loop of radius r is placed at the center of current carrying conducting square loop of side a. If both loops are coplanar and a >> r, then the mutual inductance between the loops will be
View Solution
