A long wire carries a current of uniform density. Let i be the total current carried by the wire. Show that the magnetic energy per unit length stored within the wire equals μ0t216π . Note that it does not depend on the wire diameter.
Video Solution
Text Solution
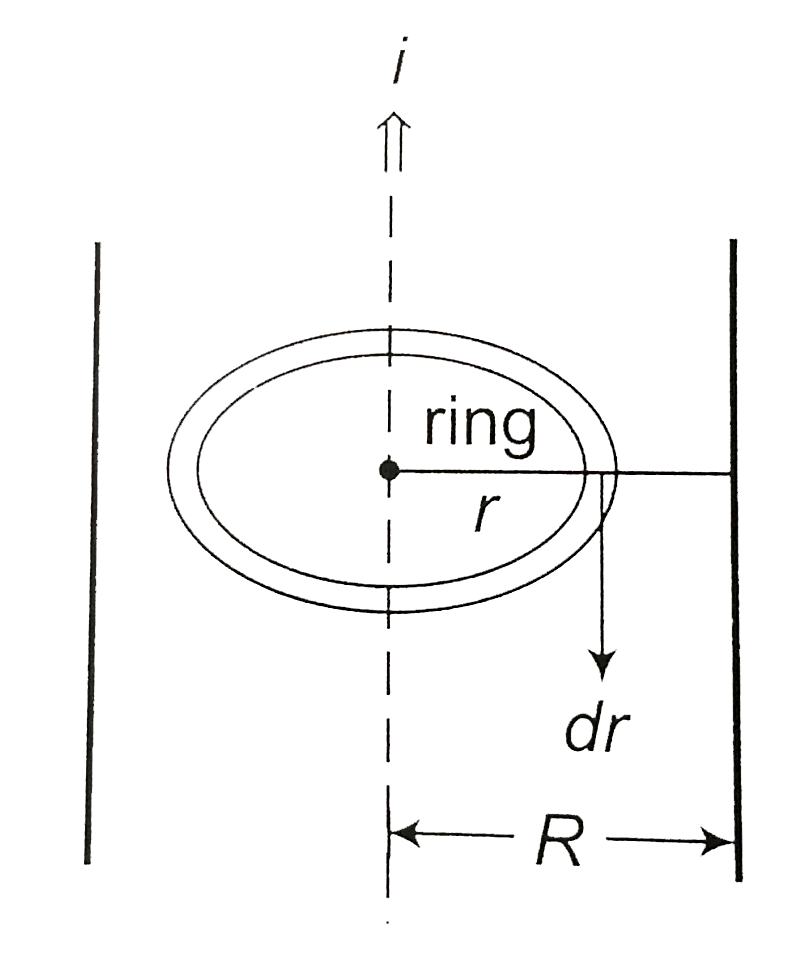
Consider a ring of radius r and thickness dr . dA=2πrdr
B=μ0ir2πR2
uB22μ0=μ20t2r22μ0.4π2R4=μ0i2r28π2R4
Consider unit length of wire
dV=dA×1=2πrdr
dU=udV=μ0i2r28ππ2R4.2πrdr
=μ0i2r3dr4πR4
U=μ0i24πR4∫R0r3dr=μ0i216π
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
For the current carrying wire, show that the magnetic field at P is
 Aμ0i4π(3π2R+√2d)⊙Bμ0i4π(3π2R−√2d)⊗Cμ0i4π(3π2R−√2d)⊙Dμ0i4π(3π2R+√2d)⊗
Aμ0i4π(3π2R+√2d)⊙Bμ0i4π(3π2R−√2d)⊗Cμ0i4π(3π2R−√2d)⊙Dμ0i4π(3π2R+√2d)⊗The resistance of a current carrying wire depends on
Athe area of cross-section of the conducting wire.Bthe length of conducting wire.Cthe material of the wire.DAll the above capacitorTwo parallel wires carrying current 1 A and 3 A respectively are 1 m apart. If the current is in opposite direction, the force per unit length on both the wires will be:
A6×10−5 repulsiveB6×10−5Nm attractiveC6×10−7Nm repulsiveD6×10−5Nm attractive
A long straight wire carries a current of 35A. What is the magnetic of the field →B at a point 20cm from the wire?
View SolutionA long copper wire carries a current of 10 ampere . Calculate the magnetic flux per metre of the wire for a plane surface S inside the wire as shown in the figure.
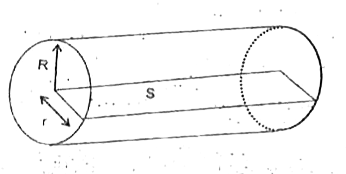
View SolutionA long copper wire carries a current of I ampere. Calculate the magnetic flux per meter of the wire for a plane surface S inside the wire as shown in Fig.

View SolutionThe direction of the force on a current carrying wire placed in a magnetic field depends on
View SolutionThe direction of the force on a current carrying wire placed in a magnetic field depends on
View Solution
