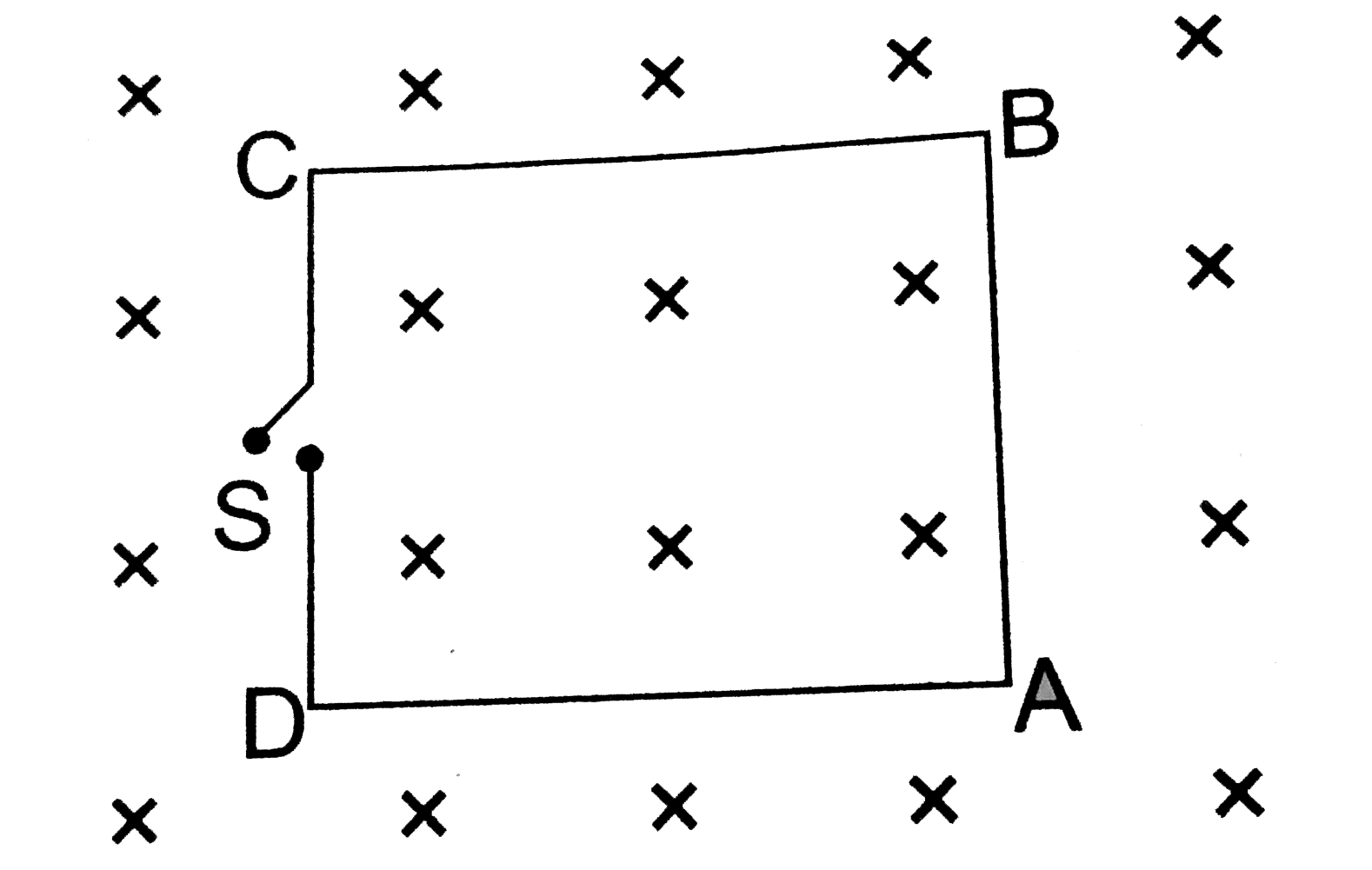
The magnetic field in the cylindrical region shown in figure increases at a constant rate of 20.0mT/sec . Each side of the square loop abcd and defa has a length of I.00cm and a resistance of 4.00Ω . Find the cuurent (magnitude and sense) in the wire ad if:
(a) the switch SI is closed but S2 is open
(b) SI is but S2 is closed
(c) both SI and S2 are open and
(d) both SI and S2 are closed
(a)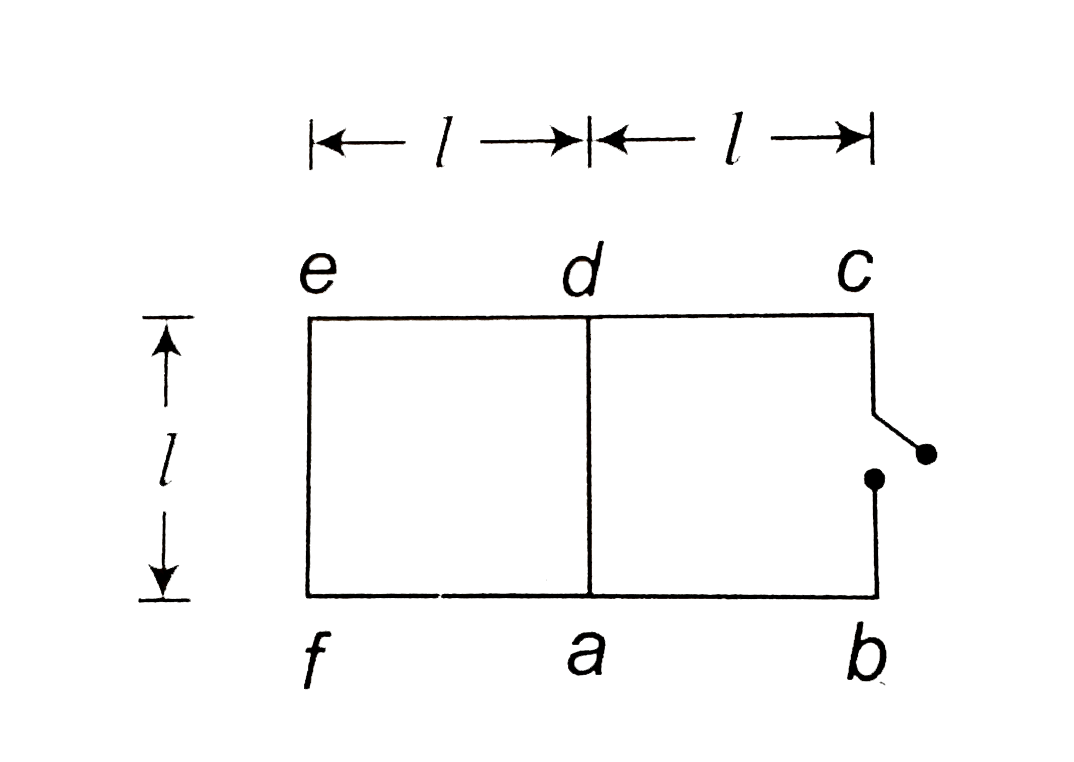 
dBdt=20mT/sec=20×10−3T/sec
Flux through loop adef
ϕ=BA
e=dϕdt=dBdtl2
=(20×10−3)(1×10−2)2=20×10−7V
Resistance of loop R=4×4=16Ω
Current in the loop I=eR=20×10−716=1.25×10−7A
Since flux is increasing, induced current will be anticlockwise i.e. a to b
(b) Same current, anticlockwise in the loop abcd , d to a
(c) No current
(d) Current in ad : zero
Topper's Solved these Questions
Similar Questions
The magnetic field in the cylinderical region shown in figure increases at a constant rate of 10.0mT/s Each side of the square loop abcd and defa has a length of 2.00 cm and resistance of 2.00Ω. Correctly match the current in the wire 'ad' in four different situations as listed in column-I with the values given in column-II
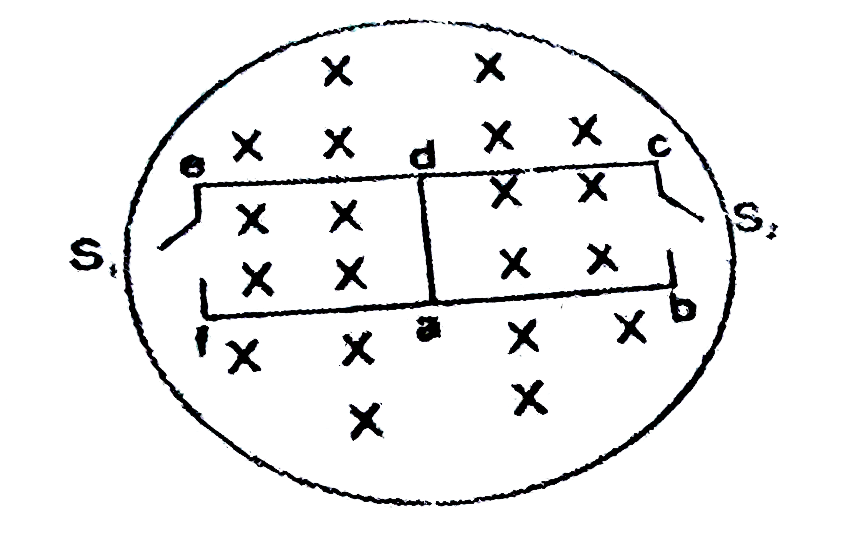
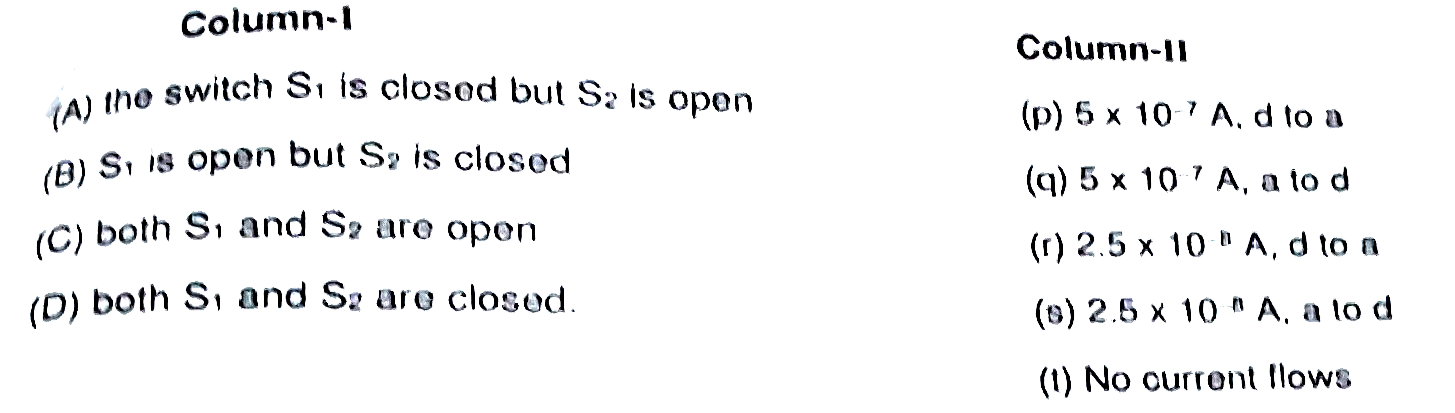
View SolutionFind heat produced in the circuit shown in figure on closing the switch S.
View Solution
Knowledge Check
- Question 1 - Select One
The magnetic field in the cylindrical region shown in figure increase at a constant rate of 20mT/sec. Each side of the square loop ABCD has a length of 1cm and resistance of 4Ω. Find the current in the wire AB if the switch S is closed
A1.25×10−7A,(anticlockwise)B1.25×10−7A (clockwise)C2.5×10−7A(anticlockwise)D2.5×10−7A(clockwise) - Question 2 - Select One
In the circuit shown in figure, switch S is initially closed and S is open. Find V-V
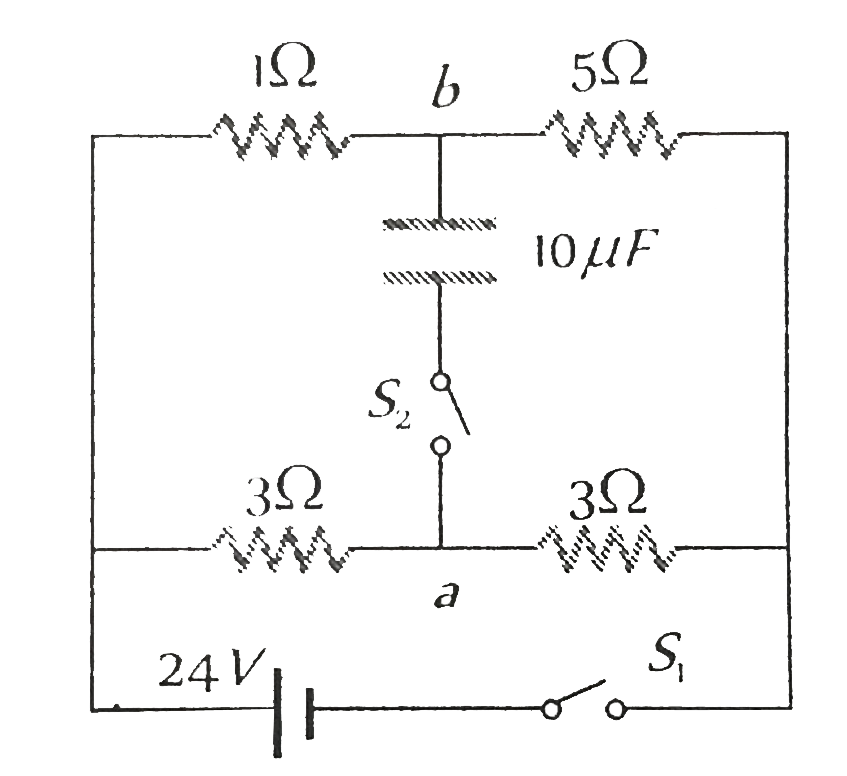A4VB8VC12VD16V - Question 3 - Select One
In the circuit shown in the figure The steady state currents i1andi2 in the coils after the switch S is closed are
Ai1=EL2R(L1+L2)Bi1=EL1R(L1+L2)Ci2=EL2R(L1+L2)Di2=E√L1L2RL2
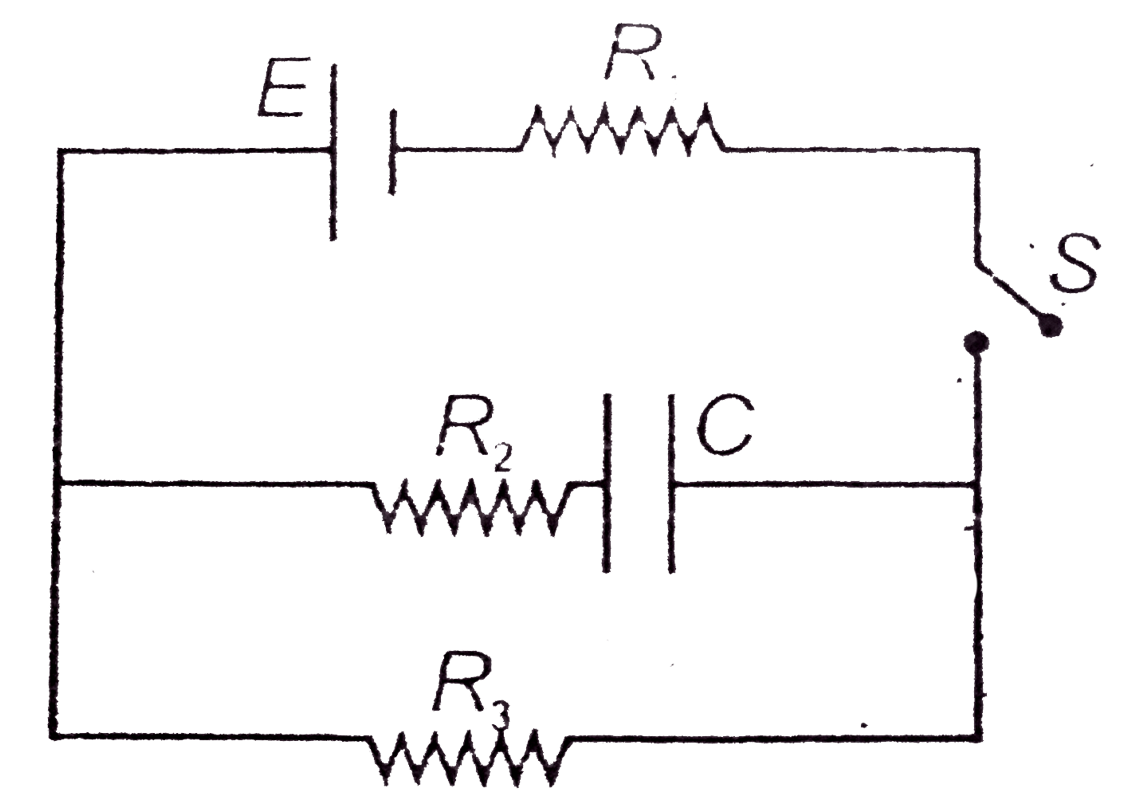
Find time constant of the circuit when (a) S is closed . (b) S is open.
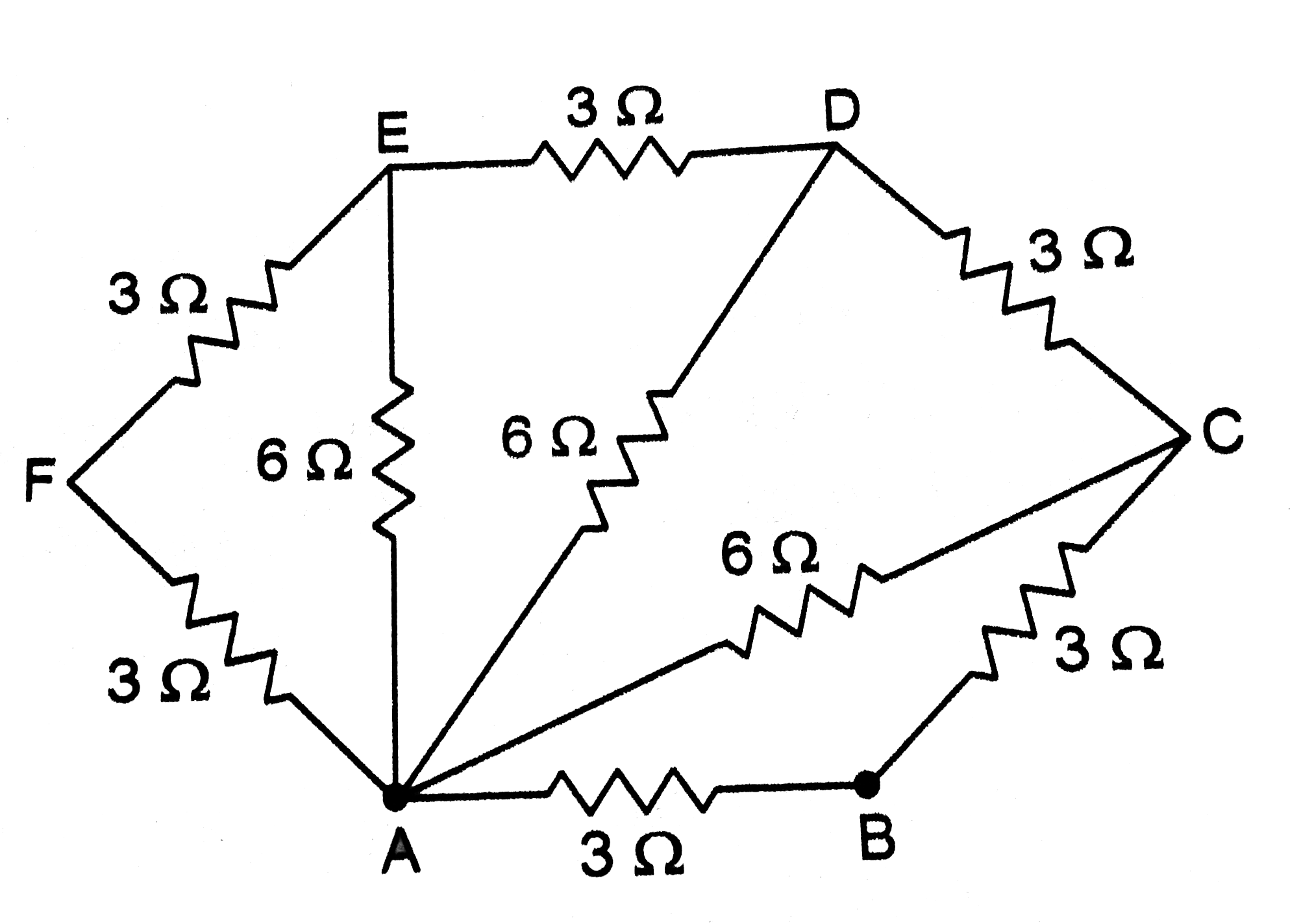
View SolutionFind the equivalent resistance of the network shown in figure between the points a and b when (a) the switch S is open and (b) the switch S is closed .
View SolutionIn given circuit initially switch Sw1 is closed and Sw2 is open, Now Sw1 is opened and Sw2 is closed, what is the heat liberated in resistance R?
View SolutionIn the circuit shown in figure-3.238, find the current in 6Ω resistance just after closing the switch S.
View SolutionFind the effective resistance of the network shown in Fig.4.15 between the points A and B when (i) the switch S is open (ii) switch S is closed.
View Solution