In Thomson's experiment for determining e/m the potential different between the cathod and the anod (in accelerating coloumns ) is same as that between the deflecting plates (in the regions of crossed field ) . If thep.d is doubled , by what factor should the magnetic field be increased to ensure that the electron beam remains undeflected
12mυ2=V.q,12m(EB)2=V.q,12mV2d2B2=V.q
qm=V2d2B2,B2αV→Bα√V,B1α√2V
B1=√2B
Topper's Solved these Questions
- ATOMIC PHYSICSBook:NARAYNAChapter:ATOMIC PHYSICSExercise:C.U.Q
Explore 88 Videos
- ATOMIC PHYSICSBook:NARAYNAChapter:ATOMIC PHYSICSExercise:LEVEL-I (C.W)
Explore 23 Videos
- ALTERNATING CURRENTBook:NARAYNAChapter:ALTERNATING CURRENTExercise:LEVEL - II(H.W)
Explore 13 Videos
- ATOMS Book:NARAYNAChapter:ATOMS Exercise:EXERCISE -4
Explore 47 Videos
Similar Questions
An electron is accelerated through a potential difference of 1000V and directed into space between two parallel plates separated by 2cm with a potential difference of 100V applied across them. If the electron enters perpendicular to the electric field between the polates, what magnetic field perpendicular to both the electron path and the electric field will be neccessary so that the electron may travel undeflected. Take e=1.6×10−19C and m=9×1031kg.
View SolutionBoth, the electric and magnetic fields can deflect a moving electron. What is the difference between these deflections?
View Solution
Knowledge Check
In the experiments for determination of e /m of electrons by Thomson method electric and magnetic fields are
Aparallel and both are perpendicualr to the motion of the electronBboth mutually parallel and also parallel to the motion of the electronCboth mutually perpendicular and also perpendicular to the motion of the electronDboth mutually perpendicualr and have no relation with the motionof the electronIn an experiment to measure the charge on an electrons , the electrons travelling at a speed of 1.825×107 m/s are subjected to a deflecting electric field 3.2×104 V/m . The intensity of magnetic field applied so that the beam remains undeflected is
A1.7×10−3Wb/m2B7.1×10−3Wb/m2C1.7×103Wb/m2D7.1×103Wb/m2Following experiment was performed by J.J. Thomson in order to measure ratio of charge e and mass m of electron.
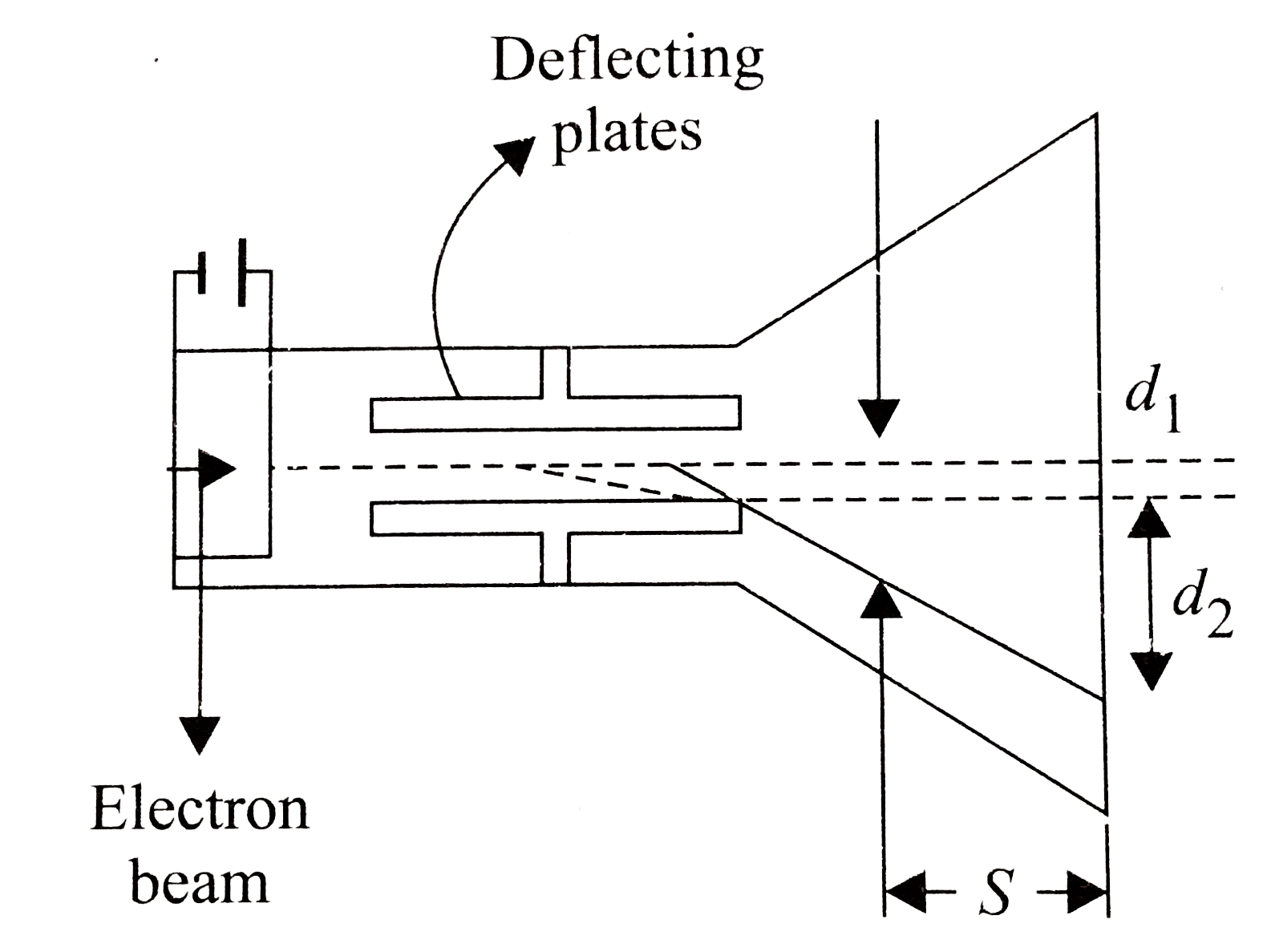
Electrons emitted from a hot filament are accelerated by a potential difference V. As the electrons pass through deflecting plates, they encounter both electric and magnetic fields. the entire region in which electrons leave the plates they enters a field free region that extends to fluorescent screen. The entire region in which electrons travel is evacuated.
Firstly, electric and magnetic fields were made zero and position of undeflected electron beam on the screen was noted. The electric field was turned on and resulting deflection was noted. Deflection is given by d1=eEL22mV2 where L = length of deflecting plate and v = speed of electron.
In second part of experiment, magnetic field was adjusted so as to exactly cancel the electric force leaving the electron beam undeflected. This gives eE=evB. Using expression for d1 we can find out em=2d1EB2L2
A beam of electron with velocity 3×107ms−1 is deflected 2 mm while passing through 10 cm in an electric field of 1800V/m perpendicular to its path. e/m for electron isA1.5×1011Ckg−1B2×1011Ckg−1C2.5×1011Ckg−1D3×1011Ckg−1
The figure shows the schematic of an absolute electrometer. The potential difference that is to be measured is applied between the plates 1and2, with the upper plate connected to one arm of a balance beam.* The pan connected to the other arm is loaded with weights until balance is achieved, that is, when the upper plate begins to move upward. In this way the force acting between the charged plates is measured, and this enables one to determine the magnitude of the potential di fference between the plates. It the aquiltbrium in the electrometer stable or unstable? • The figure does not show the protecting rings around plates 1 and 2 with the same potentials. Theso are used to ensure that the field is as uniform as possible
View SolutionIn photoelectric effect experiment potential difference between plates increases keeping incident light on cathode plate remains unchanged which of the following is correct about saturation current :
View SolutionFollowing experiment was performed by J.J. Thomson in order to measure ratio of charge e and mass m of electron.
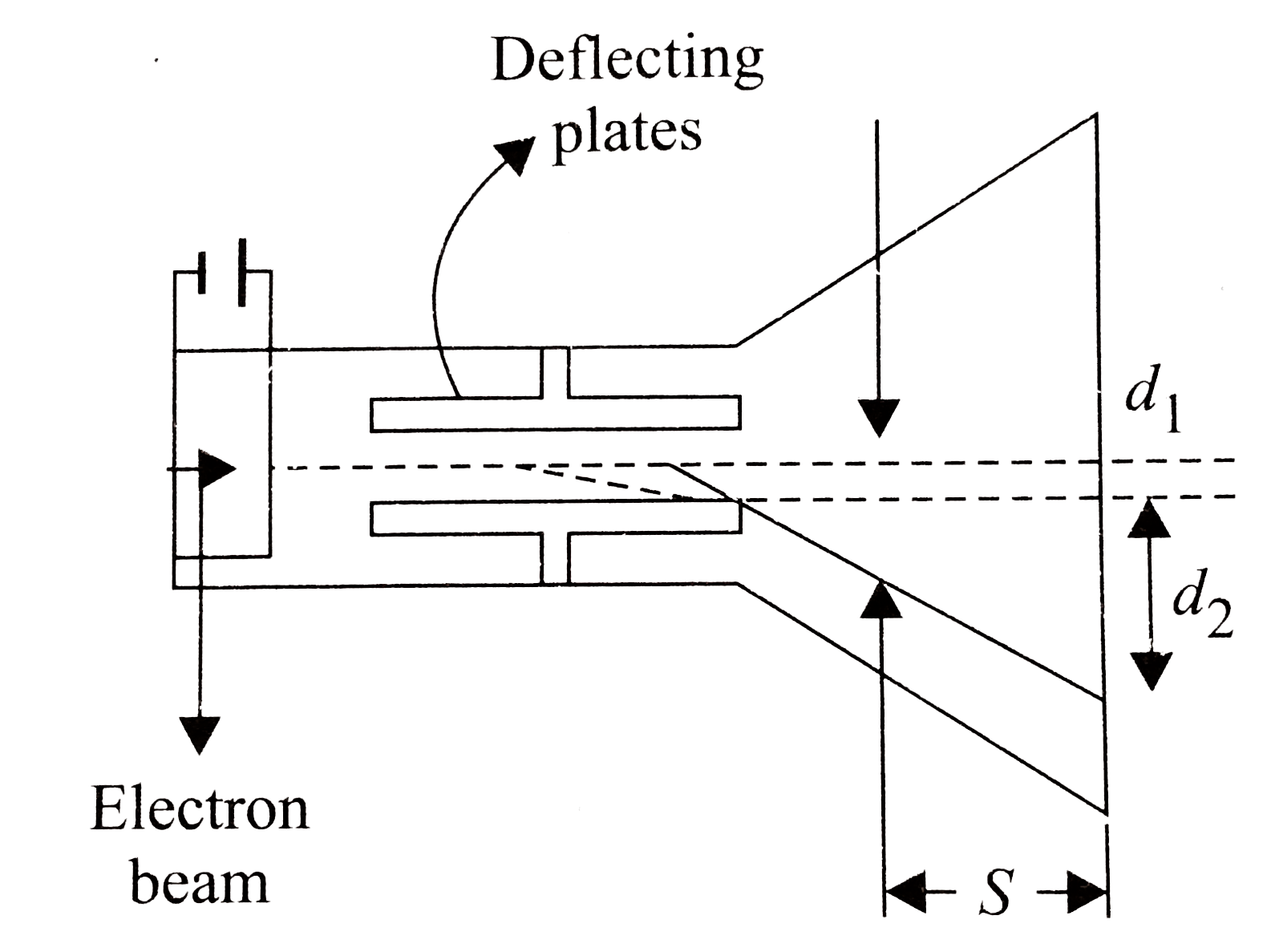
Electrons emitted from a hot filament are accelerated by a potential difference V. As the electrons pass through deflecting plates, they encounter both electric and magnetic fields. the entire region in which electrons leave the plates they enters a field free region that extends to fluorescent screen. The entire region in which electrons travel is evacuated.
Firstly, electric and magnetic fields were made zero and position of undeflected electron beam on the screen was noted. The electric field was turned on and resulting deflection was noted. Deflection is given by d1=eEL22mV2 where L = length of deflecting plate and v = speed of electron.
In second part of experiment, magnetic field was adjusted so as to exactly cancel the electric force leaving the electron beam undeflected. This gives eE = evB. Using expression for d1 we can find out em=2d1EB2L2
If the electron is deflected downward when only electric field is turned on, in what direction do the electric and magnetic fields point in second part of experiment
View SolutionFollowing experiment was performed by J.J. Thomson in order to measure ratio of charge e and mass m of electron.
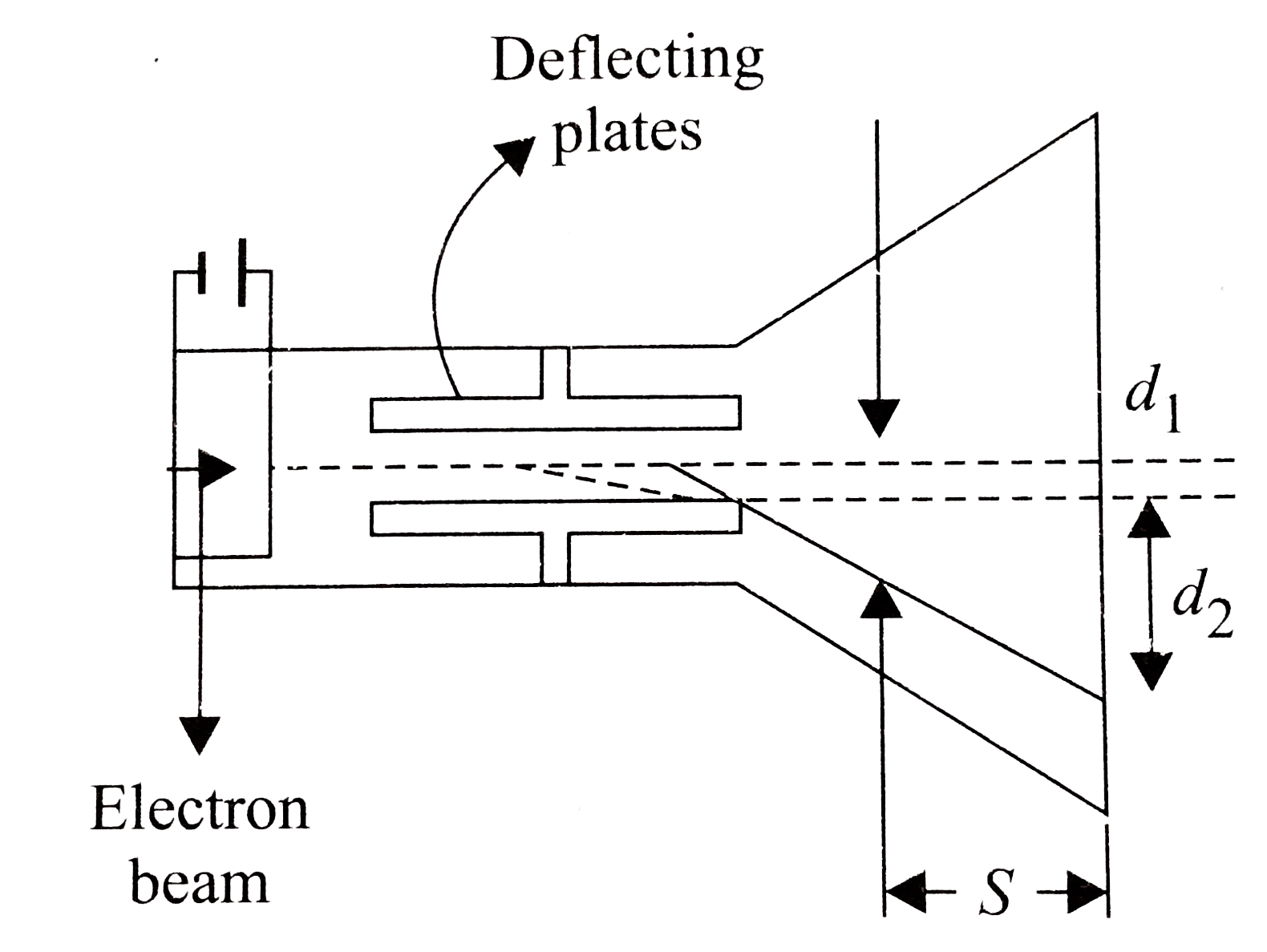
Electrons emitted from a hot filament are accelerated by a potential difference V. As the electrons pass through deflecting plates, they encounter both electric and magnetic fields. the entire region in which electrons leave the plates they enters a field free region that extends to fluorescent screen. The entire region in which electrons travel is evacuated.
Firstly, electric and magnetic fields were made zero and position of undeflected electron beam on the screen was noted. The electric field was turned on and resulting deflection was noted. Deflection is given by d1=eEL22mV2 where L = length of deflecting plate and v = speed of electron.
In second part of experiment, magnetic field was adjusted so as to exactly cancel the electric force leaving the electron beam undeflected. This gives eE=evB. Using expression for d1 we can find out em=2d1EB2L2
If the electron speed were doubled by increasing the potential differece V, which of the following would be true in order to correctly measure e/m
View SolutionWhen an electron is accelerated through a potential difference V, it experience a fromce F through as uniform transverse magnetic field. If the potential difference is increased to 2V, the force experoenced by the electron in the same magnetic field is
View Solution

