The sides of a triangle are 50cm,78cmand112cm The smallest altitude is
(a) 20cm
(b) 30cm
(c) 40cm
(d) 50cm
Let the sides of the triangles be a=50cm,b=78cmandc=112cm
semiperimeter of the triangle, s=a+b+c2
s=50+78+1122
s=120
Now, area of triangle by using heron's formula = (s√(s−a)(s−b)(s−c))
(120√(120−50)(120−78)(120−112))
1680cm2
∴ area of triangle = 12×base×height
1680=12×112×altitude
altitude=30cm
Hence, option (b) is correct.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If the sides of a triangle are 50 m, 78 m and 112 m, then the perpendicular distance from the opposite angle on the side 112 m is
A10 mB30 mC5 mD20 mIf the sides of a triangle are 50 m, 78 m and 112 m, then the perpendicular distance from the opposite angle on the side 112 m is
A10 mB30 mC5 mD20 m
If the diagonals of a rhombus are 18cm and 24cm respectively, then its side is equal to
(a)16cm (b) 15cm (c) 20cm (d) 17cm
View SolutionIn an isosceles triangle ABC , if AB=AC=25cm and BC=14cm , then the measure of altitude from A on BC is (a) 20cm (b) 22cm (c) 18cm (d) 24cm
View SolutionThe area of a circle is 220 cm2 . The area of a square inscribed in it is (a) 49 cm2 (b) 70 cm2 (c) 140 cm2 (d) 150 cm2
View SolutionThe area of the circle that can be inscribed in a square of side 10 cm is (a) 40π cm2 (b) 30π cm2 (c) 100 π cm2 (d) 25 π cm2
View SolutionThe perimeter of a triangle is 30 cm and the circumference of its incircle is 88 cm. The area of the triangle is (a) 70 cm2 (b) 140 cm2 (c) 210 cm2 (d) 420 cm2
View SolutionIn Figure, if AC is bisector fo ∠BAD such that AB=3 cm and AC=5 cm, then CD= 2 cm (b) 3 cm (c) 4 cm (d) 5 cm
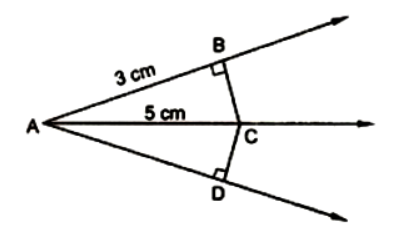
View Solution
