Find the coordinates of the points which divides the line segment joining the points (6, 3) and (−4, 5) in the ratio 3 :2 internally.
(i) Given points are A (6,3) and B(-4,5). Let poitn P(x,y) divide AB internally in the ratio 3:2

∴(x,y)≡(3(−4)+2(6)3+2,3(5)+2(3)3+2)≡(0,215)
(ii) P(x,y) divides AB externally in the ratio 3:2.
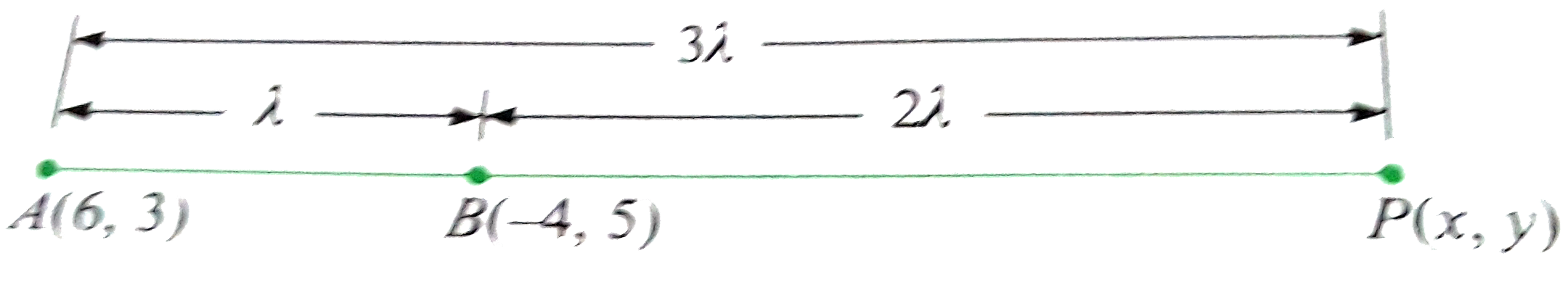
∴(x,y)≡(3(−4)−2(6)3−2,3(5)−2(3)3−2)≡(−24,9)
Alternatively, ABBP=(12) (From the figure)
∴(−4,5)≡(3(6)+1(x)2+1,2(3)+1(y)2+1)≡(12+x3,6+y3)
∴(x,y)≡(−24,9)
Topper's Solved these Questions
Similar Questions
Knowledge Check
Find the coordinates of the point which divides the line segment joining the points A(5,−2) and B(9,6) in the ratio 3:1
A(8,4)B(2,4)C(7,−4)D(7,5)
Find the coordinates of the point which divides the line segment joining the points A(4, -3) and B(9, 7) in the ratio: 3:2.
View SolutionFind the coordinates of the point which divies the line segment joining the points (1, 3, 5) and
(-2, 1, 0) in the ratio 1 : 2 internally.
View SolutionInternal division + proof + example :-Find the coordinates of a point which devides the line segments joining the points (6;2) and (-4;5) in the ratio 3:2 internally .
View SolutionFind the coordinates of the point which divides the line segment joining the points (4, 3) and (8, 5)in the ratio 3 : 1 internally.
View SolutionFind the coordinates of the point which divides the line segments joining the points (6,3) and (−4,5) in the ratio 3:2 (i) internally and (ii) externally.
View SolutionFind the co-ordinates of the point which divides the line segment joining the points (4,-3) and (8,5) in the ratio 1:3 internally
View SolutionFind the coordinates of the point which divides the line segment joining the points (1, 5, 3) and
(-2, 3, 4) in the ration 3:4 (i) internally, and (ii) externally.
View Solution

