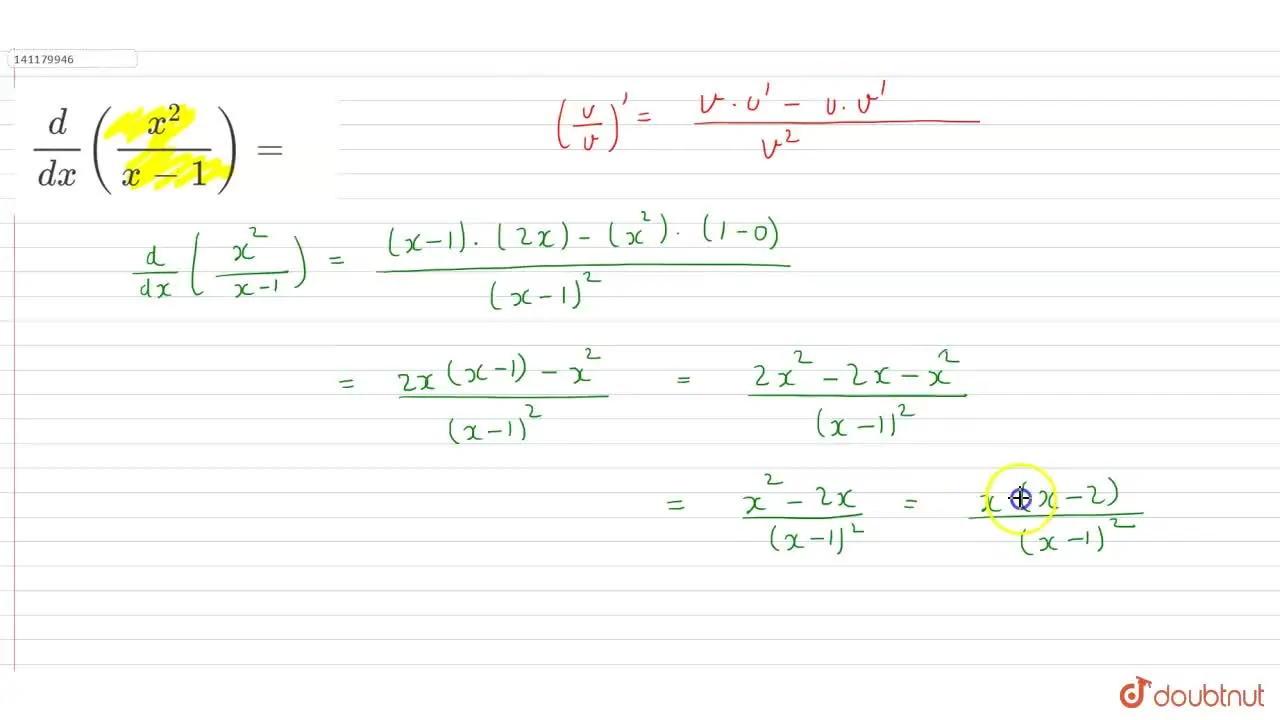ddx(x2x−1)=
A
1+1(x−1)2
B
1(x−1)2−1
C
1−1(x−1)2
D
−1(x−1)2
Video Solution
Text Solution
The correct Answer is:C
|
Answer
Step by step video, text & image solution for (d)/(dx)((x^(2))/(x-1))= by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023
Related Playlists
- BOOK - MARVEL PUBLICATIONCHAPTER - DIFFERENTIATIONEXERCISE - MULTIPLE CHOICE QUESTIONS (TEST YOUR GRASP - I : CHAPTER 11)19videos
DIFFERENTIATION
- BOOK - MARVEL PUBLICATIONCHAPTER - DIFFERENTIATIONEXERCISE - MULTIPLE CHOICE QUESTIONS (TEST YOUR GRASP - II : CHAPTER 11)24videos
DIFFERENTIATION
- BOOK - MARVEL PUBLICATIONCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - TEST YOUR GRASP14videos
DIFFERENTIAL EQUATIONS
- BOOK - MARVEL PUBLICATIONCHAPTER - INTEGRATION - DEFINITE INTEGRALS EXERCISE - TEST YOUR GRASP20videos
INTEGRATION - DEFINITE INTEGRALS