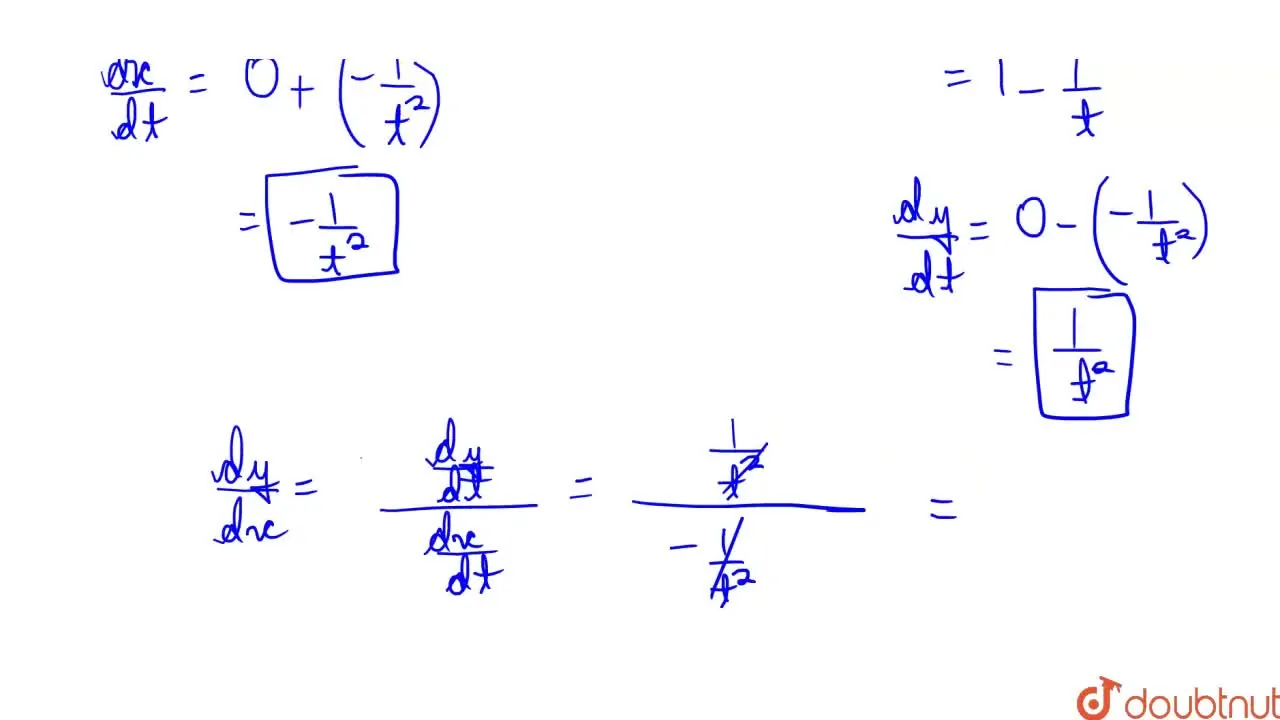If x=t+1t,y=t−1t, then dydx=
A
1
B
0
C
2
D
−1
Video Solution
Text Solution
The correct Answer is:D
|
Answer
Step by step video, text & image solution for If x=(t+1)/(t),y=(t-1)/(t)," then "(dy)/(dx)= by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023
Related Playlists
- BOOK - MARVEL PUBLICATIONCHAPTER - DIFFERENTIATIONEXERCISE - MULTIPLE CHOICE QUESTIONS (TEST YOUR GRASP - I : CHAPTER 11)19videos
DIFFERENTIATION
- BOOK - MARVEL PUBLICATIONCHAPTER - DIFFERENTIATIONEXERCISE - MULTIPLE CHOICE QUESTIONS (TEST YOUR GRASP - II : CHAPTER 11)24videos
DIFFERENTIATION
- BOOK - MARVEL PUBLICATIONCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - TEST YOUR GRASP14videos
DIFFERENTIAL EQUATIONS
- BOOK - MARVEL PUBLICATIONCHAPTER - INTEGRATION - DEFINITE INTEGRALS EXERCISE - TEST YOUR GRASP20videos
INTEGRATION - DEFINITE INTEGRALS
Similar Questions
If x=t+1t,y=t−1t then d2ydx2 at t = 1
View SolutionIf x=t2+1t2,y=t−1t, then dydx=
View SolutionIf x=a(t+t−1),y=a(t−t−1), then dydx=
View SolutionIf x=a(t−1t),y=a(t+1t),show that dydx=xy
View SolutionIf y=t2−t+1, then: dydx=
View SolutionIf x=cos−1t,y=log(1−t2), then (dydx) at t=12 is
View SolutionIf x=a(t−sint),y=a(1−cost), then dydx is equal to
View SolutionIf x=2t1+t2,y=1−t21+t2, then dydx=
View SolutionIf x=t⋅logt and y=tt, then: dydx=
View SolutionIf x=(t+1t)a,y=at+1t,f i n ddydx
View Solution