Which one of the following is a correct statement ? If →Pand→Q are two non zero vectors of different magnitudes, then
→P×→Q=→Q×→P
→P⋅→Q=−→Q⋅→P
→P+→Q=→Q+→P
→P−→Q=→Q−→P
The correct Answer is:C
In the addition of vectors, order of vectors is immaterial.
∴→P+→Q=→Q+→P is a correct statement.
(c ) is the correct option. Vector addition is commutative but vector subtraction is non-commutative.
Similarly →P×→Q=−→Q×→Pand→P⋅→Q=→Q⋅→P
Thus (a) and (b) are wrong.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Which one of the following is correct ? If the vector →c is normal to the vectors →aand→b, then →c, is :
Aparallel to both →a+→band→a−→bB→a−→band parallel to →a+→bCnormal to →a+→b and parallel to →a−→bDnormal to both →a+→band→a−→bIf →A and →B are two vectors, which of the following is not correct?
A→A+→B=→B+→AB→A.→B=→B.→AC→A×→B=→B×→AD→A−→B=−(→B−→A)The maximum value of the magnitude of the resultant of two vectors →Pand→Q is 24 units and the minimum value of the magnitude of their resultant is 4 units. What is the ratio of the magnitudes of the vectors →Pand→Q ?
A34B45C65D75
→a,→b,→c are three coplanar unit vectors such that →a+→b+→c=0. If three vectors →p,→q,and→r are parallel to →a,→b,and→c, respectively, and have integral but different magnitudes, then among the following options, |→p+→q+→r| can take a value equal to a. 1 b. 0 c. √3 d. 2
View SolutionIf →aand →bare two collinear vectors, then which of the following are incorrect:(A) →b=λ→a,for some scalar lambda (B) →a=±→b (C) the respective components of →aand →bare proportional (D) both the vectors →a and →b have same direction, but different magnitudes.
View SolutionThe cross product of two vectors gives a vector perpendicular to the plane containing the vectors.
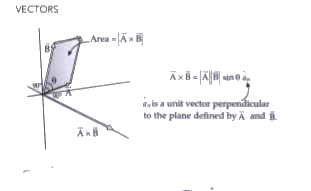
If →a and →b are non-zero vectors, then →a⋅(→a×→b)= _________
View SolutionAnswer the following :
(i) Can 2 similar vectors of different magnitude yield a zero resultant? Can 3 yield?
(ii) Can →a+→b=→a−→b?
(iii) If →a+→b=→c & |→a|+∣∣→b∣∣=|→c|. What further information you can have about these vectors.
(iv) If →a & →b are two non zero vectors such that ∣∣→a+→b∣∣=∣∣→a+→b∣∣, then what is the angle between →a & →b.
(v) Time has a magnitude & direction. Is it a vector?
(iv) When will →a×→b=→a.→b?
(vii) Does the unit vectors →i,→j & →k have units?
View SolutionIf vec(a) is a vector and x is a non-zero scalar, then
View Solution
