In the following network of 5 branches, the respective current are l1,l2,l3 etc. given that l1=−0.5A,l4=1A and l5=0.5A, the remaining currents are
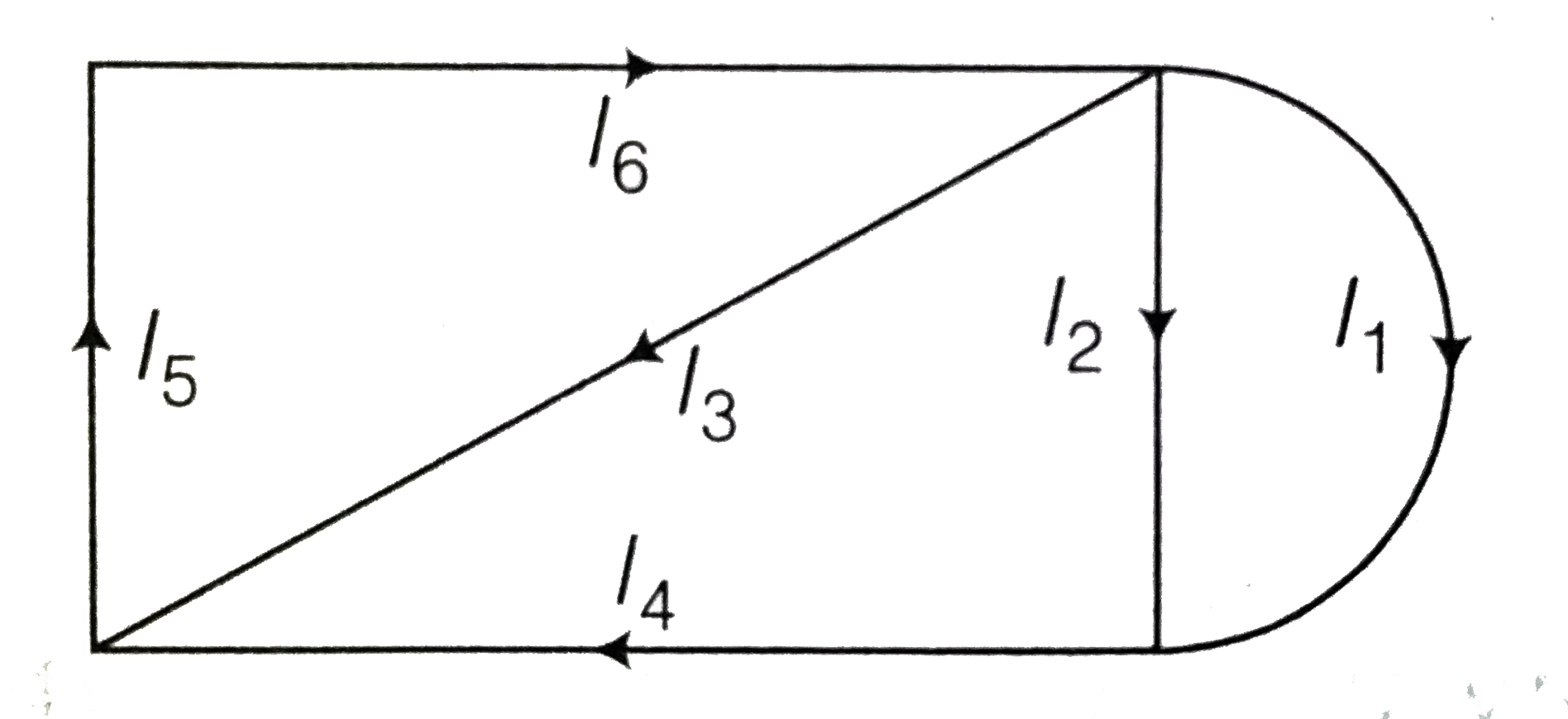
I2=−1.5A,I3=0.5A,I6=0.5A
I2=1.5A,I3=−0.5A,I6=0.5A
I2=1.5A,I3=0.5A,I6=−0.5A
I2=1.5A,I3=0.5A,I6=0.5A
The correct Answer is:B
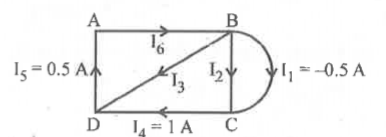
To find the currents in the various branches, we use Kirchhoff's current law.
At C,I1+I2=I4
∴I2=I4−I1=1−(−0.5)=1.5A
and at the junction D,
I3+I4=I5
∴I3=I5−I4=0.5−1=0.5A
and I5=I6=0.5A as the current is not divided at A
Thus I2=1.5A,I3=−0.5AandI6=0.5A
Topper's Solved these Questions
Similar Questions
Knowledge Check
The currents l, lZ and lL are respectively :-
A15 mA, 5 mA, 10 mAB15 mA, 7.5 mA, 7.5 mAC12.5 mA, 5 mA, 7.5 mAD12.5 mA, 7.5 mA, 5 mATwo alternating current are given by
l1=l0 sin ωtand l l_(2)=l_(0) cos (omega +phi)
The ratio of rms value isA0.042361111111111B1:ϕC0.043055555555556Dnon of theseThe three lines l1=4x−3y+2=0,l2=3x+4y−4=0 and l3=x−7y+6=0
Aform a rt. angled isosceles triangleBform a rt. Angled triangleCare concurrentDNone
Equation of the circumcircle of a triangle formed by the lines L1=0,L2=0andL3=0 can be written as L1L2+λL2L3+μL3L1=0, where λandμ are such that coefficient of x2 =coefficient of y2 and coefficient of xy=0.
If L1L2+λL2L3+μL3L1=0 is such that μ=0andλ is non-zero, then it represents
View SolutionEquation of the circumcircle of a triangle formed by the lines L1=0,L2=0andL3=0 can be written as L1L2+λL2L3+μL3L1=0, where λandμ are such that coefficient of x2 =coefficient of y2 and coefficient of xy=0.
L1L22+λL2L23+μL21=0 represents
View SolutionGiven : li=44.2±=0.1 and l2=23.1±0.1 the uncertainty in l1+l2 is
View SolutionLet L be the set of all straight lines in plane. l1 and l2 are two lines in the set. R1,R2 and R3 are defined relations.
(i) l1R1l2:l1 is parallel to l2
(ii) l1R2l2:l1 is perpendicular to l2
(iii) l1R3l2:l1 intersects l2
Then which of the following is true ?
View SolutionThe correct statement about ICl5 and ICl−4 is:
View Solution