If V1andV2 are stopping potentials for incident photons of wavelengths λ1andλ2 for same cathode material, then Planck's constant is given by [e = charge on electron, c = speed of light]
ec(V2−V1)λ1λ2λ1−λ2
ec(λ1−λ2)V1V2V1−V2
ecV2V1λ1λ2
ec(λ1+λ2)(V1+V2)
The correct Answer is:A
Step by step video, text & image solution for If V_1 and V_2 are stopping potentials for incident photons of wavelengths lambda_1 andlambda_2 for same cathode material, then Planck's constant is given by [e = charge on electron, c = speed of light] by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTRONS AND PHOTONSBook:TARGET PUBLICATIONChapter:ELECTRONS AND PHOTONSExercise:Competitive Thinking
Explore 78 Videos
- ELECTRONS AND PHOTONSBook:TARGET PUBLICATIONChapter:ELECTRONS AND PHOTONSExercise:Evaluation Test
Explore 19 Videos
- ELECTRONS AND PHOTONSBook:TARGET PUBLICATIONChapter:ELECTRONS AND PHOTONSExercise:Evaluation Test
Explore 19 Videos
- COMMUNICATION SYSTEMSBook:TARGET PUBLICATIONChapter:COMMUNICATION SYSTEMSExercise:Evaluation Test
Explore 15 Videos
- FORCE Book:TARGET PUBLICATIONChapter:FORCE Exercise:Evaluation Test
Explore 16 Videos
Similar Questions
In a photoelectric experiment using a sodium surface, you find a stopping potential of 1.85 V for a wavelength of 300 nm and a stopping potential of 0.820 V for a wavelength of 400 nm. From these data find (a) a value for the Planck constant, (b) the work function Φ for sodium, and (c) the cutoff wavelength λ0 for sodium.
View SolutionWhen light of wavelength λ is incident on a metal surface, stopping potential is found to be x. When light of wavelength nλ is incident on the same metal surface, stopping potential is found to be xn+1 . Find the threshold wavelength of the metal.
View Solution
Knowledge Check
The maximum velocity of an electron emitted by light of wavelength λ incident on the surface of a metal of work function ϕ, is
Where h = Planck's constant , m = mass of electron and c = speed of light.A[2(hc+λϕ)mλ]1/2B2(hc−λϕ)mC[2(hc−λϕ)mλ]1/2D[2(hλ−ϕ)m]1/2The stopping potential for photoelectrons from a metal surface is V1 when monochromatic light of frequency υ1 is incident on it. The stopping potential becomes V2 when monochromatic light of another frequency is incident on the same metal surface. If h be the Planck’s constant and e be the charge of an electron, then the frequency of light in the second case is:
Aυ1−eh(V2+V1)Bυ1+eh(V2+V1)Cυ1−eh(V2−V1)Dυ1+eh(V2−V1)When photon of wavelength λ1 are incident on an isolated shere supended by an insulated , the corresponding stopping potential is found to be V. When photon of wavelength λ2 are used , the orresponding stopping potential was thrice the above value. If light of wavelength λ3 is used , carculate the stopping potential for this case.
Ahce[1λ3+12λ2−1λ1]Bhce[1λ3+12λ2−3λ1]Chce[1λ3+1λ2−1λ1]Dhce[1λ3−1λ2−1λ1]
Using the graph shown in fig for stopping potential vs the incident frequency of photons, calculate Planck's constant.
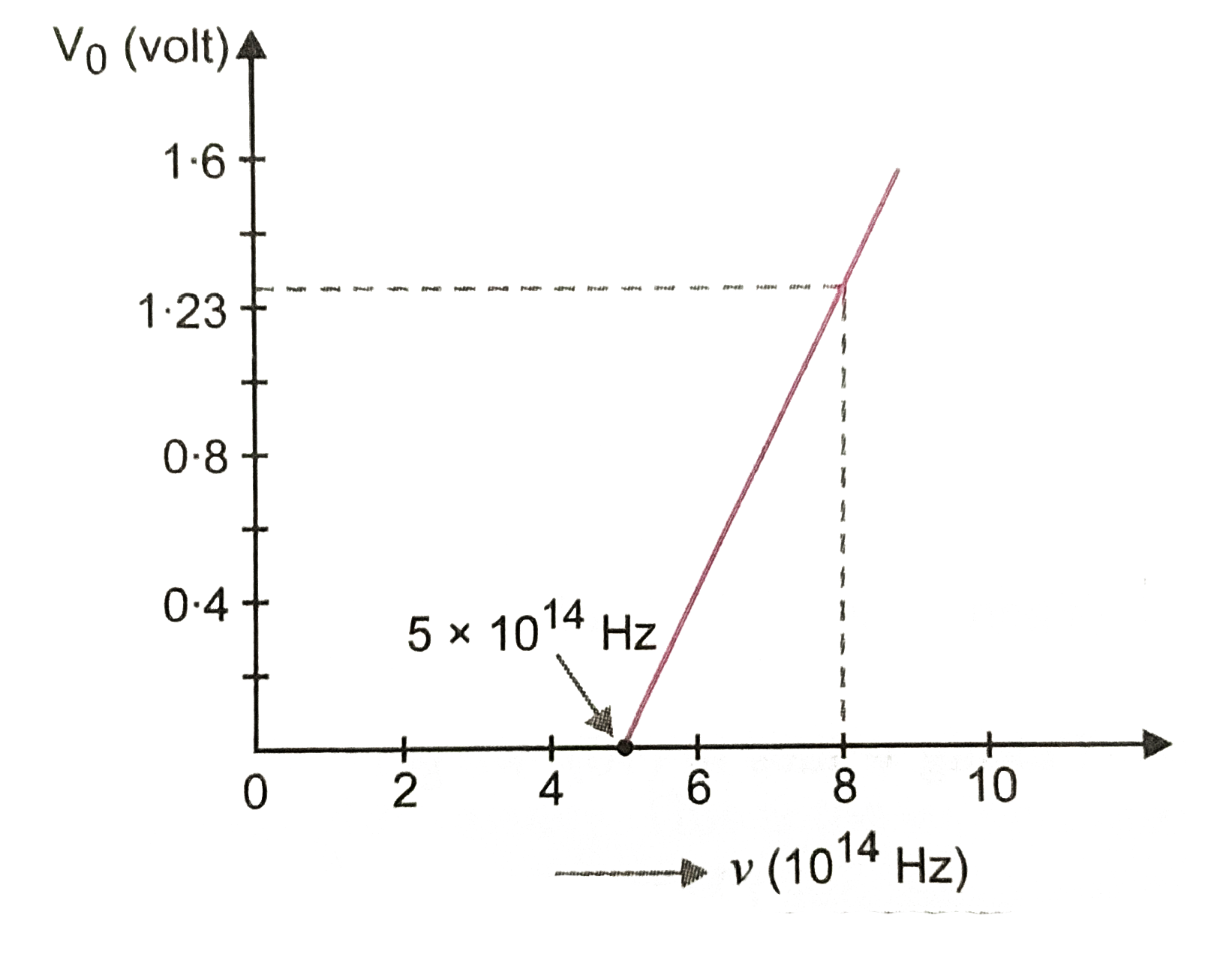
View SolutionThe energy of a photon of wavelength λ is given by
View SolutionWhen light of wavelength λ is incident on photosensitive surface, the stopping potential is V. When light of wavelength 3λ is incident on same surface, the stopping potential is V6Thereshould wave length for the surface is
View SolutionThe energy of a photon of wavelength λ is [ h = Planck's constant, c = speed of light in vacuum ]
View SolutionWhen a photosensitive surface is illuminated with light of wavelength λ, the stopping potential is V0. But when light of wavelength 2λ is incident on the same surface, the stopping potential is V04. What is the threshold wavelength for the surface ?
View Solution