Two identical light sources S1 and S2 emit light of same wavelength λ. These light rays will exhibit interference if
phase differences remain constant.
phases are distributed randomly
ligh intensities remain constant.
light intensities change radomly.
The correct Answer is:A
NA
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTIONBOOK - TARGET PUBLICATIONCHAPTER - INTERFERENCE AND DIFFRACTIONEXERCISE - CRITICAL THINKING
72 Videos
- INTERFERENCE AND DIFFRACTIONBOOK - TARGET PUBLICATIONCHAPTER - INTERFERENCE AND DIFFRACTIONEXERCISE - COMPETITIVE THINKING
117 Videos
- GRAVITATIONBOOK - TARGET PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - EVALUATION TEST
24 Videos
- KINETIC THEORY OF GASES AND RADIATION BOOK - TARGET PUBLICATIONCHAPTER - KINETIC THEORY OF GASES AND RADIATION EXERCISE - Evaluation test
18 Videos
Similar Questions
Two coherent point sources S1 and S2 vibrating in phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S1 and perpendicular to line S1S2. Find the position of farthest and nearest minima.
 .
.
View SolutionTwo coherent point sources S1andS2 vibrating in phase emit light of wavelength λ . The separation between them is 2λ . The light is collected on a screen placed at a distance D>>λ from the slit S1 as shown. The minimum distance, so that intensity at P is equal to the intensity at O

View Solution
Knowledge Check
Two coherent point sources S1 and S2 vibrating in phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S2 and perpendicular to line S1S2. Find the position of farthest and nearest minima.
 .A7λ12B15λ4Cλ2D3λ4
.A7λ12B15λ4Cλ2D3λ4Choose the most appropriate option.
Two coherent point sources S1andS2 vibrating in phase emit light of wavelength λ. The separation between them is 2λ. The light is collected ona screen placed at a distance D>>λ from the slit S1 as shown. The minimum distance, so that intensity at P is equal to intensity at O.
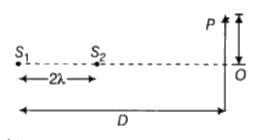 A√2DB√3DC√8DD√5D
A√2DB√3DC√8DD√5DFollowing figures shows sources S1 and S2 that emits light of wavelength λ in all directions. The sources are exactly in phase and are separated by a distance equal to 1.5λ. If we start at the indicated start point and travel along path 1 and 2, the interference produce a maxima all along
 A(a) Path 1B(b) Path 2C(c) Any pathD(d) None of these
A(a) Path 1B(b) Path 2C(c) Any pathD(d) None of these
Two coherent point source S1 and S2 vibrating in phase emit light of wavelength λ. The separation between them is 2λ as shown in figure. The first bright fringe is formed at 'P' due to interference on a screen placed at distance 'D' from S1(D>>λ), then OP is

1) √3D,2)1.5D,3)√2D,4)2D
View SolutionTwo identical narrow slits S1andS2 are illuminated by the light of a wavelengthλ from a point source P. If , as shown in the diagram above , the light is then allowed to fall on a screen , and if n is a positive integer , the condition for destructive interference at Q is
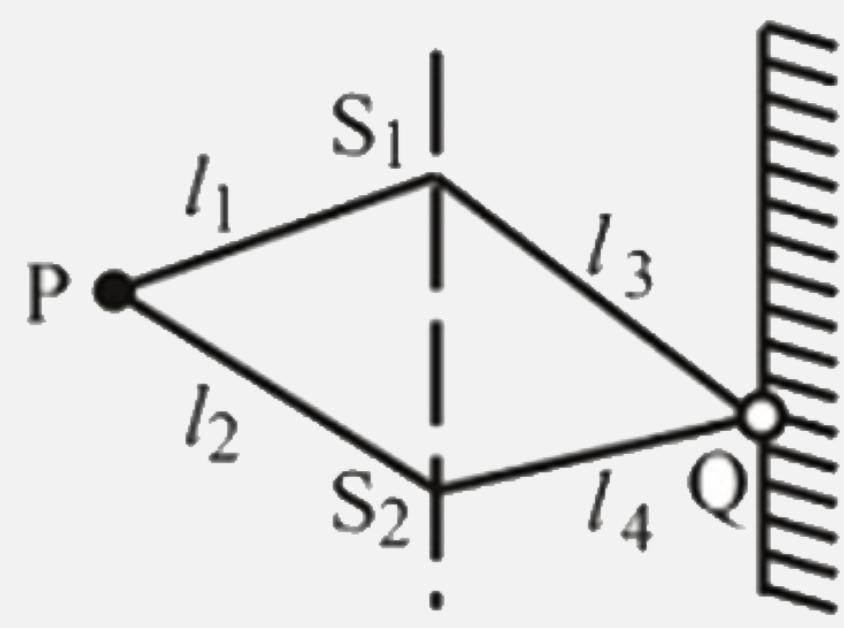
View SolutionSources 1 and 2 emit lights of different wavelengths whereas sources 3 and 4 emit light of different intensities.
The coherence
View SolutionTwo identical narrow slits S1 and S2 are illuminated by light of wavelength λ from a point source P. If, as shown in the diagtam above the light is then allowed to fall on a scree, and if n is a positive integer, the condition for destructive interference at Q is that

View SolutionWhen a point light source, of power W, emiting monochromatic light of wavelength λ is kept at a distance a from a small photosensitive surface of work function ϕ and area S. Then
View Solution
