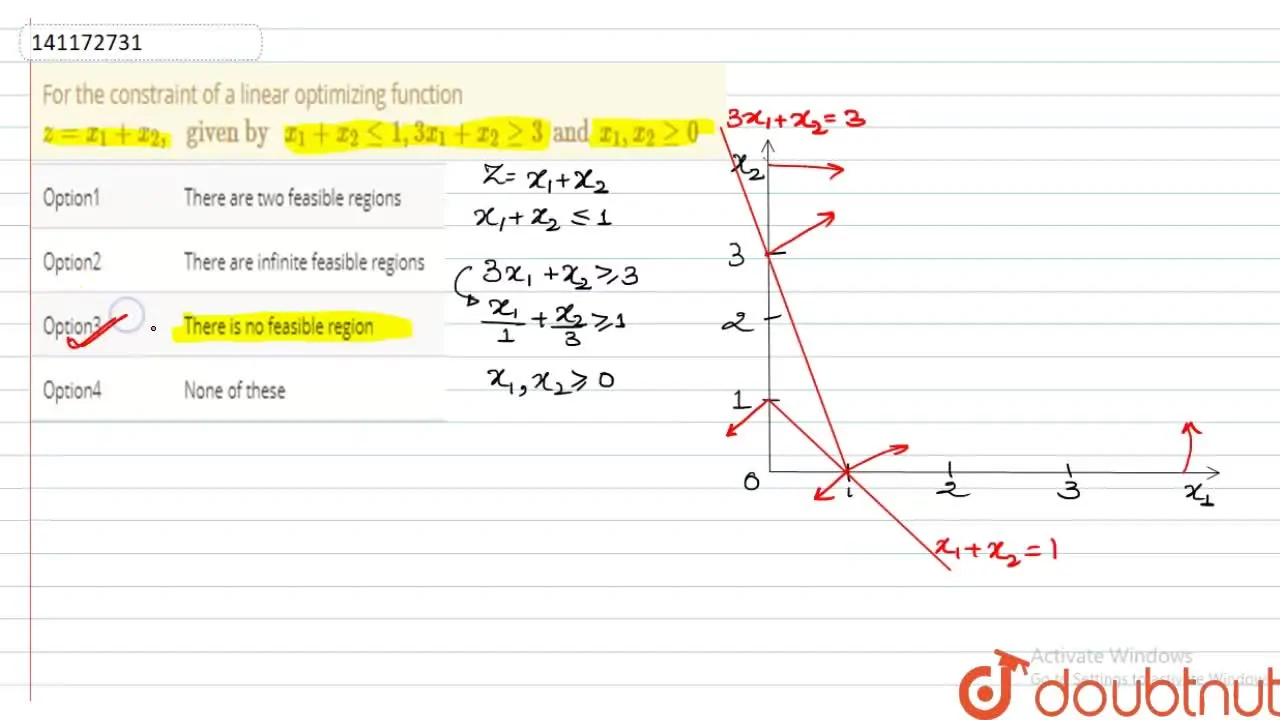
For the constraint of a linear optimizing function z=x1+x2, given by x1+x2≤1,3x1+x2≥3andx1,x2≥0
There are two feasible regions
There are infinite feasible regions
There is no feasible region
None of these
The correct Answer is:C
Step by step video, text & image solution for For the constraint of a linear optimizing function z=x_(1)+x_(2) , " given by " x_(1)+x_(2)le1,3x_(1)+x_(2)ge3 and x_(1),x_(2)ge0 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - TARGET PUBLICATIONCHAPTER - LINEAR PROGRAMMINGEXERCISE - Competitive Thinking
35 Videos
- LINEAR PROGRAMMINGBOOK - TARGET PUBLICATIONCHAPTER - LINEAR PROGRAMMINGEXERCISE - Evaluation Test
11 Videos
- LINEAR PROGRAMMINGBOOK - TARGET PUBLICATIONCHAPTER - LINEAR PROGRAMMINGEXERCISE - Evaluation Test
11 Videos
- LINEBOOK - TARGET PUBLICATIONCHAPTER - LINEEXERCISE - Evaluation Test
1 Videos
- MATHEMATICAL LOGIC BOOK - TARGET PUBLICATIONCHAPTER - MATHEMATICAL LOGIC EXERCISE - EVALUATION TEST
14 Videos
Similar Questions
Knowledge Check
The LPP problem Max z=x1+x2 such that −2x1+x2≤1,x1≤2,x1+x2≤3andx1,x2≥0 has
AOne solutionBThree solutionsCInfinite number of solutionsDNo solutionFor the LPP Min z=x1+x2 such that inequalities
5x1+10x2≥0,x1+x2≤1,x2≤4 and x−1,x2≥0AThere is a baunded solutionBThereis no solutionCThere are infinite solutionsDNone of the aboveThe minimum value of Z=2x1+3x2, subject to the constraints 2x1+7x2≥22,x1+x2≥6,5x1+x2≥10 and x1,x2≥0, is
A14B20C10D16
Maximize z=−x1+2x2
Subject to
−x1+x2≤1
−x1+2x2≤4
x1,x2≤0
View SolutionMinimize z=−x1+2x2
Subject to
−x1+3x2≤10
x1+x2≤6
x1−x2≤2
and x1,x2≥0
View SolutionFind graphically the solution sets of each of the following systems of inequalities :
3x1+x2≤66
x1+x2≤45
x1≤20
x2≤40
and x1,x2≥10
View SolutionFind graphically the solution sets of each of the following systems of inequalities :
x1+x2≤6
x1≥3
2x1+3x2≥3
x1≥0,x2≥0
View SolutionThe objective function Z=4x1+5x2, Subject to 2x1+x2≥7,2x1+3x2≤15,x2≤3,x1,x2≥0 has minimum value at the point
View Solution