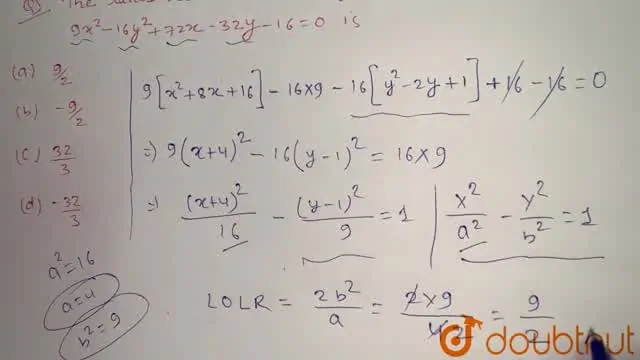The latus rectum of the hyperbola 9x2−16y2+72x−32y−16=0 is
92
−92
323
−323
The correct Answer is:A
Step by step video, text & image solution for The latus rectum of the hyperbola 9x ^(2) -16 y^(2) + 72x - 32y-16=0 is by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
- BOOK - TARGET PUBLICATIONCHAPTER - CIRCLE AND CONICS EXERCISE - COMPETITIVE THINKING158videos
CIRCLE AND CONICS
- BOOK - TARGET PUBLICATIONCHAPTER - CIRCLE AND CONICS EXERCISE - EVALUATION TEST28videos
CIRCLE AND CONICS
- BOOK - TARGET PUBLICATIONCHAPTER - CIRCLE AND CONICS EXERCISE - EVALUATION TEST28videos
CIRCLE AND CONICS
- BOOK - TARGET PUBLICATIONCHAPTER - FACTORIZATION FORMULAEEXERCISE - EVALUATION TEST8videos
FACTORIZATION FORMULAE
Similar Questions
The latus rectum of the hyperbola 16x2−9y2=144 is 16/3 b. 32/3 c. 8/3 d. 4/3
View SolutionThe eccentricity of the hyperbola 9x2−16y2+72x−32y−16=0, is
View SolutionThe latus -rectum of the hyperbola 16x2−9y2=576 is 645
View SolutionThe length of the latus rectum of the hyperbola 9y2−4x2=36 will be-
View SolutionFind the length of axes, eccentricity, centre, foci and latus rectum of the hyperbola 16x2−3y2−32x−12y−44=0.
View SolutionLet l1 be the length of the latus rectum of the parabola 9x2−6x+36y+19=0. Let l2, be the length of the latus rectum of the hyperbola 9x2−16y2−18x−32y−151=0. Let n be the unit digit in the product of l1andl2. The number of terms in the binomial expansion of (1+x)n is
View SolutionThe foci of the hyperbola 9x2−16y2+18x+32y−151=0 are
View SolutionFind the eccentricity, length of a latus rectum, equations of the latus rectum of the hyperbola x216−y29=1.
View SolutionThe length of the transverse axis of the hyperbola 9x2−16y2−18x−32y−151=0 is
View SolutionThe length of the latus rectum of the hyperbola 3x2−y2=4 is
View Solution