If in greatest integer function, the domain is a set of real numbers, then range will be set of
Real numbers
Rational numbers
Imaginary numbers
Intergers
The correct Answer is:D
Step by step video, text & image solution for If in greatest integer function, the domain is a set of real numbers, then range will be set of by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SETS, RELATIONS AND FUNCTIONSBOOK - TARGET PUBLICATIONCHAPTER - SETS, RELATIONS AND FUNCTIONSEXERCISE - COMPETITVE THINKING
170 Videos
- SETS, RELATIONS AND FUNCTIONSBOOK - TARGET PUBLICATIONCHAPTER - SETS, RELATIONS AND FUNCTIONSEXERCISE - EVALUATION TEST
14 Videos
- SETS, RELATIONS AND FUNCTIONSBOOK - TARGET PUBLICATIONCHAPTER - SETS, RELATIONS AND FUNCTIONSEXERCISE - EVALUATION TEST
14 Videos
- PROBABILITYBOOK - TARGET PUBLICATIONCHAPTER - PROBABILITYEXERCISE - EVALUATION TEST
8 Videos
- STRAIGHT LINE BOOK - TARGET PUBLICATIONCHAPTER - STRAIGHT LINE EXERCISE - EVALUATION TEST
10 Videos
Similar Questions
Consider the following function in the set of real numbers R
View SolutionTwo friends A&B were discussing about domain of greatest integer function y=[x] ,then A said that domain of [x] is R (set of real numbers).Then B expressed that he has doubt in finding the domain of f(x)=1√[x]−x. Then domain of f(x)=1√[x]−x is
View Solution
Knowledge Check
If rangr of funtion f(x) whose domain is set of all real numbers is [−2,4], then range of function g(x)=12f(2x+1) is equal to
A[−2,4]B[−1,2]C[−3,9]D[−2,2]If rang of fraction f(x) whose domain is set of all real numbers is [−2,4], then range of functiong(x)=12f(2x+1) is equal to :
A[−2,4]B[−1,.2]C[−3,9]D[−2,2]A functions from the set of natural numbers to integers defined by
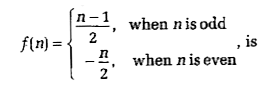 Aone-one but not ontoBonto but not one-oneCone-one and onto bothDnone of these
Aone-one but not ontoBonto but not one-oneCone-one and onto bothDnone of these
If R is the set of Positive rational number and E is the set of real numbers, then
View SolutionIf [.] denotes the greatest integer function then the domain of the real-valued function log[x+12]∣∣x2−x−2∣∣ is
View SolutionIf the function f(x)=[2.6+bsinx] where [.] denotes greatest integer function, is an even function then complete set of values of b is:
View Solution[2x]−2[x]=λ where [.] represents greatest integer function and {.} represents fractional part of a real number then
View SolutionIf f(x)=[x]sin(π[x+1]), where [.] denotes the greatest integer function, then the set of point of discontiuity of f in its domain is
View Solution
