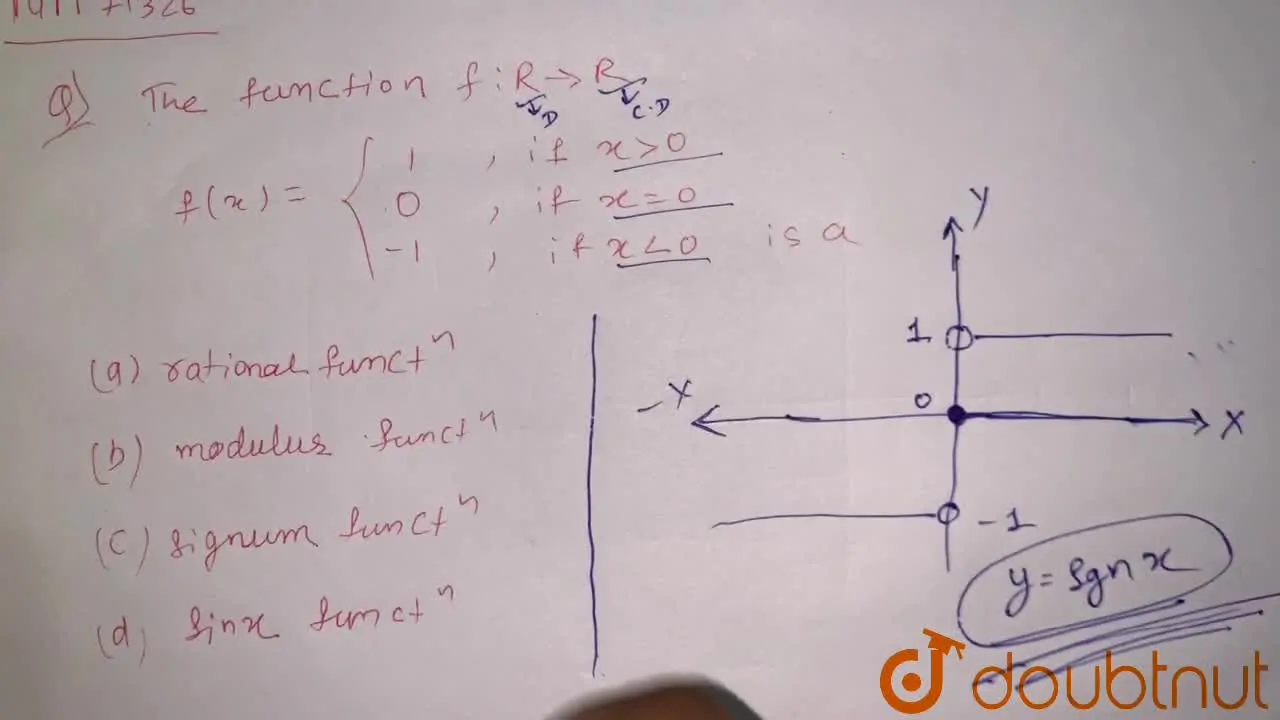
The function
f:R→R:f(x)=1ifx>0 =0ifx=0 =−1ifx<0isa
rational function
modulus function
signum function
sinx function
The correct Answer is:B
Step by step video, text & image solution for The function {:(f:R to R:f(x) = 1, if x gt 0),(" "= 0, if x =0),(" "=-1, if x lt0is a):} by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
- BOOK - TARGET PUBLICATIONCHAPTER - SETS, RELATIONS AND FUNCTIONSEXERCISE - CRITICAL THINKING83videos
SETS, RELATIONS AND FUNCTIONS
- BOOK - TARGET PUBLICATIONCHAPTER - SETS, RELATIONS AND FUNCTIONSEXERCISE - COMPETITVE THINKING170videos
SETS, RELATIONS AND FUNCTIONS
- BOOK - TARGET PUBLICATIONCHAPTER - PROBABILITYEXERCISE - EVALUATION TEST8videos
PROBABILITY
- BOOK - TARGET PUBLICATIONCHAPTER - STRAIGHT LINE EXERCISE - EVALUATION TEST10videos
STRAIGHT LINE
Similar Questions
The function f is defined as :
f(x)=⎧⎪⎨⎪⎩1,x>00,x=0−1,x<0
The range of f is :View SolutionIf the function f(x)={3x<012x>0 then limx→0f(x)=
View SolutionAt x = 0 , f(x)=x−2, if x<0=1/2, if x=0=x2, if x>0⎫⎪⎬⎪⎭ is
View SolutionIf f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩x−1,x<014,x=0x2,x>0
View SolutionA function f:R→R is given by f(x)={x4(2+sin1x)x≠00x=0, then
View SolutionA function f:R→R is given by f(x)={x4(2+sin1x)x≠00x=0, then
View SolutionA function is defined as f(x)={ex,x≤0|x−1|,x>0, then f(x) is
View SolutionLet g(x)=1+x−[x]andf(x)=⎧⎪⎨⎪⎩−1,x<00,x=01,x>0, then for all x,f[g(x)] is equal to
View SolutionFind limx→0f(x), where f(x)=⎧⎪⎨⎪⎩x−1x<00x=0x=1x>0
View SolutionIf F(x)=⎧⎪⎨⎪⎩−x2+1x<00x=0x2+1x>=0, .then limx→0f(x) is
View Solution