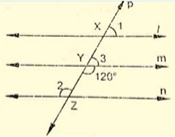
In Figure, l,mandn
are parallel lines
intersected by a transversal at X,Y,andZ
respectively. Find ∠1, ∠2 and∠3.
Give reasons.
Let∠1=3xand∠2=2x
∠1+∠2=180∘
⇒5x=180∘
x=36∘
∠1=108∘,∠2=72∘
Since m∥nand l is the intersector
∠3=∠1=108∘ and ∠4=∠2=72∘ (Opposite angles
∠7=∠5=∠2=72∘
=∠5=72∘
∠6=108∘=∠8
Let∠1=3xand∠2=2x
∠1+∠2=180∘
⇒5x=180∘
x=36∘
∠1=108∘,∠2=72∘
Since m∥nand l is the intersector
∠3=∠1=108∘ and ∠4=∠2=72∘ (Opposite angles
∠7=∠5=∠2=72∘
=∠5=72∘
∠6=108∘=∠8
Topper's Solved these Questions
Similar Questions
In Figure, l,mandn are parallel lines intersected by a transversal at X,Y,andZ respectively. Find ∠1, ∠2 and∠3. Give reasons.
Let∠1=3xand∠2=2x
∠1+∠2=180∘
⇒5x=180∘
x=36∘
∠1=108∘,∠2=72∘
Since m∥nand l is the intersector
∠3=∠1=108∘ and ∠4=∠2=72∘ (Opposite angles
∠7=∠5=∠2=72∘
=∠5=72∘
∠6=108∘=∠8
View SolutionIn Fig. 51, l, m and n are parallel lines intersected by a transversal p at X,Y and Z respectively. Find ∠1, ∠2 and ∠3. Give reasons.
View SolutionIn Fig. l, m and n are parallel lines intersected by transversal p at X, Y and Z respectively. Find ∠1, ∠2 and ∠3
View SolutionIn the given figure l∣∣m and n is transversal. If ∠5=(2x+40)∘ and ∠1=(3x+20)∘ then find the value of x and ∠5
View SolutionIn Fig.72, If lm, np and ∠1=850, find ∠2.
View SolutionIf the lines L1andL2 are tangents to 4x2−4x−24y+49=0 and are normals for x2+y2=72, then find the slopes of L1 and L2.
View SolutionBy crammer's rule,if the values of x,y and z which satisfy the system of equations x+y+z=2 ,x+2y+3z=1 ,and 3x+y-5z=4 are respectively L,M and N then 3L +5M+N=
View SolutionBy crammer's rule ,if the values of x,y and z which satisfy the system of equations x+y+z=2, x+2y+3z=1 ,and 3x+y-5z=4 are respectively L,M and N, then 3L+5M+N=
View SolutionFind the angle between the lines
5−x3=y+3−4,z=7 and x1=1−y2=z−62
View SolutionThe line segment LM is divided by point B (-7,2) in the ratio 2:1 if l (5,4) , then find the co-ordinates of M
View Solution