The maximum values of the phasors (currents and voltage) in AC circuits can be treated as vectors rotating with an angular frequency equal to the angular frequency of the rotor of the generator. If the phase difference between two phasors −→A1 and −→A2 is ϕ the resultant phasor is :
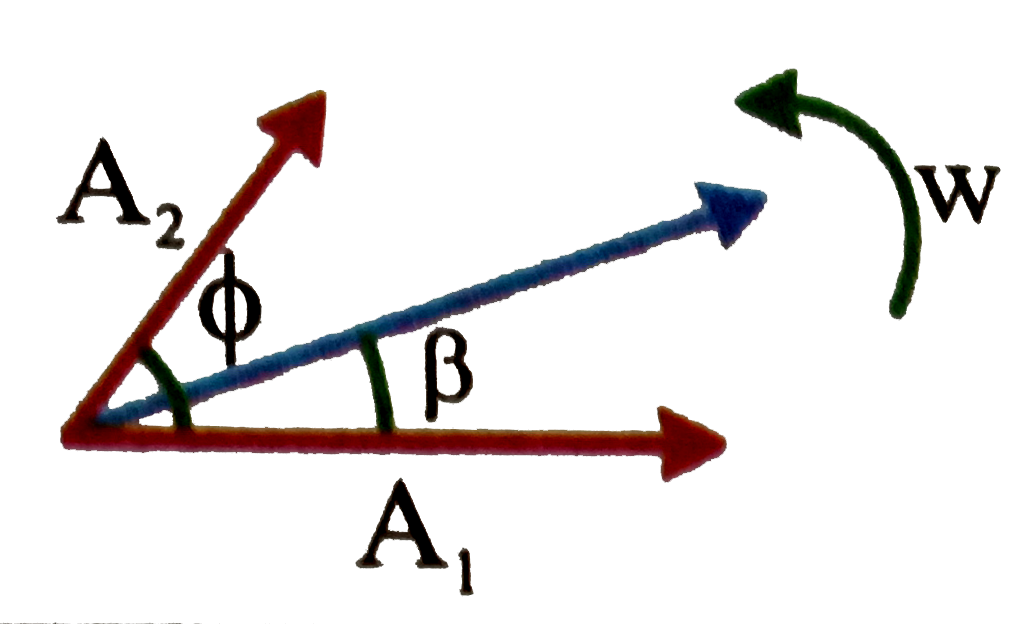
A=√A21+A22+2A1A2cosϕ
and the phase of →A with respects to A1 is
β=tan−1A2sinϕA1+A2cosϕ
RHS value
The rms value of y=f(t) is
yrms=⎧⎨⎩∫T0[f(t)]2dtT⎫⎬⎭12
Average value
The average value of y=f(t) is yav=∫T0ydtT
Using the above concept, answer the following questions.
The average value of i in i−t graph (Semi circular) is
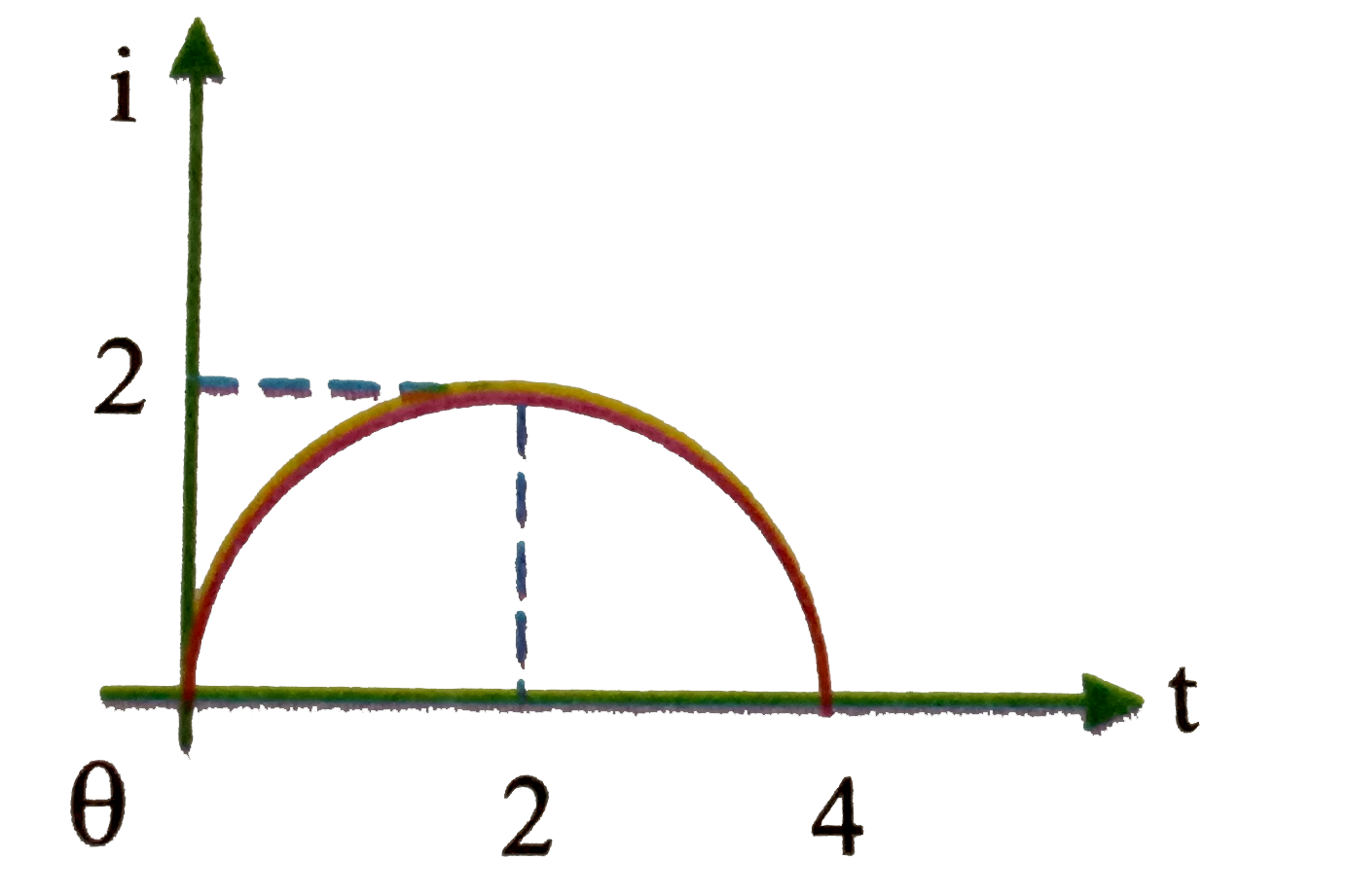
π
π2
π3
π√2
The correct Answer is:B
Step by step video, text & image solution for The maximum values of the phasors (currents and voltage) in AC circuits can be treated as vectors rotating with an angular frequency equal to the angular frequency of the rotor of the generator. If the phase difference between two phasors vec(A_(1)) and vec(A_(2)) is phi the resultant phasor is : A = sqrt(A_(1)^(2) + A_(2)^(2) + 2A_(1)A_(2) cos phi) and the phase of vec(A) with respects to A_(1) is beta = "tan"^(-1) (A_(2) sin phi)/(A_(1) + A_(2) cos phi) RHS value The rms value of y = f (t) is y_("rms") = {(int_(0)^(T) [f(t)]^(2) dt)/(T)}^((1)/(2)) Average value The average value of y = f (t) is y_(av) = (int_(0)^(T) ydt)/(T) Using the above concept, answer the following questions. The average value of i in i - t graph (Semi circular) is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - NARAYNACHAPTER - ALTERNATING CURRENTEXERCISE - LEVEL - I (H.W)
23 Videos
- ALTERNATING CURRENTBOOK - NARAYNACHAPTER - ALTERNATING CURRENTEXERCISE - LEVEL - II(H.W)
13 Videos
- ALTERNATING CURRENTBOOK - NARAYNACHAPTER - ALTERNATING CURRENTEXERCISE - LEVEL - V
83 Videos
- ATOMIC PHYSICSBOOK - NARAYNACHAPTER - ATOMIC PHYSICSEXERCISE - LEVEL-II (H.W)
14 Videos
Similar Questions
Knowledge Check
The maximum values of the phasors (currents and voltage) in AC circuits can be treated as vectors rotating with an angular frequency equal to the angular frequency of the rotor of the generator. If the phase difference between two phasors −→A1 and −→A2 is ϕ the resultant phasor is :
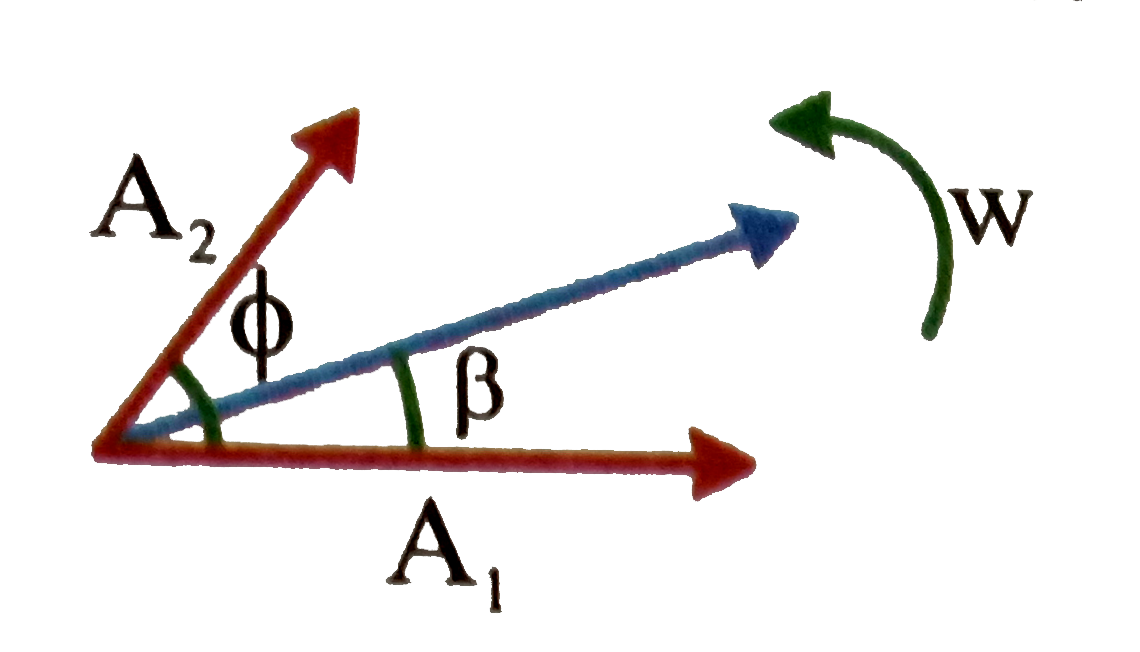
A=√A21+A22+2A1A2cosϕ
and the phase of →A with respects to A1 is
β=tan−1A2sinϕA1+A2cosϕ
RHS value
The rms value of y=f(t) is
yrms=⎧⎨⎩∫T0[f(t)]2dtT⎫⎬⎭12
Average value
The average value of y=f(t) is yav=∫T0ydtT
Using the above concept, answer the following questions.
The rms value of i3 isA2√6B√6C3√2D2√2The maximum values of the phasors (currents and voltage) in AC circuits can be treated as vectors rotating with an angular frequency equal to the angular frequency of the rotor of the generator. If the phase difference between two phasors −→A1 and −→A2 is ϕ the resultant phasor is :
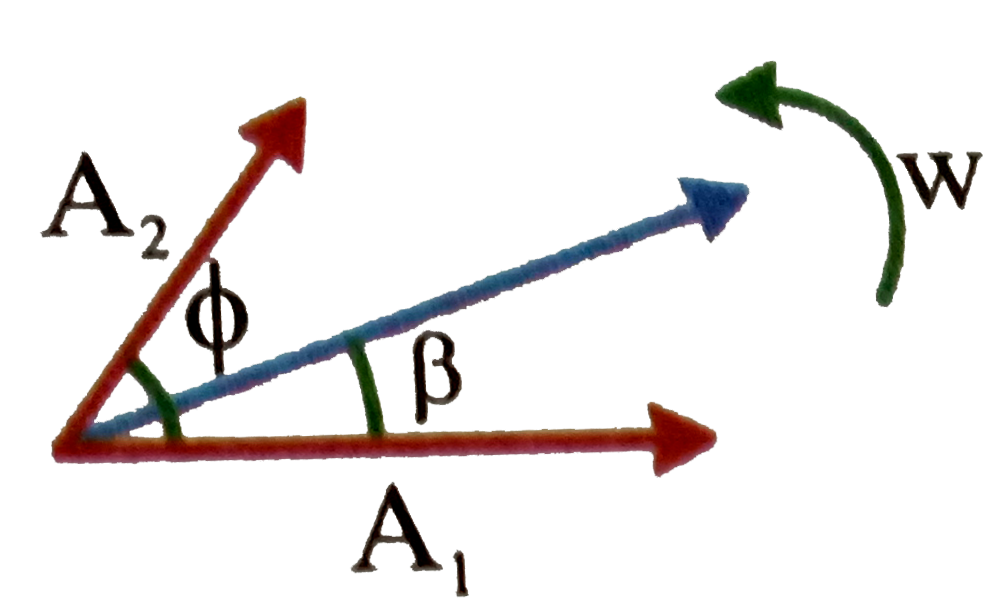
A=√A21+A22+2A1A2cosϕ
and the phase of →A with respects to A1 is
β=tan−1A2sinϕA1+A2cosϕ
RHS value
The rms value of y=f(t) is
yrms=⎧⎨⎩∫T0[f(t)]2dtT⎫⎬⎭12
Average value
The average value of y=f(t) is yav=∫T0ydtT
Using the above concept, answer the following questions.
The current i1 and i2 in A.C circuit are given as: i1=4sin(ωt−π3) and i2=4sin(ωt+π3)
The current i3 can be given as :
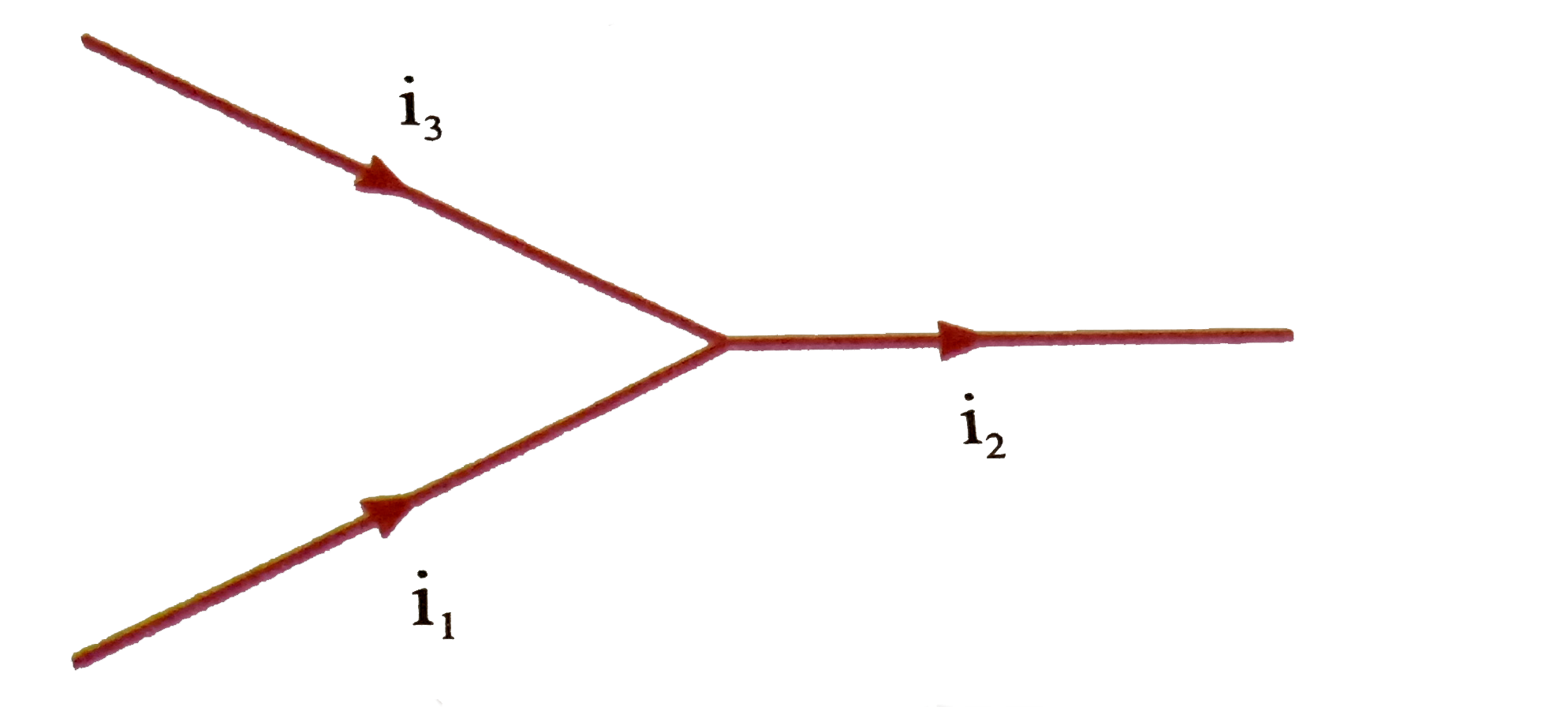 A4√3sin(ωt−2π3)B2√3cos(ωt+π3)C4sin(ωt)D4cos(ωt)
A4√3sin(ωt−2π3)B2√3cos(ωt+π3)C4sin(ωt)D4cos(ωt)Two vectors →A1and→A2 each of magnitude A are inclinded to each other such that their resultant is equal to √3A. What is the magnitude of the resultant of →A1and−→A2 is
A2AB√3AC√2ADA
If A1,A2,A3,A4 are four A.M’s between12 and 3, then prove A1+A2+A3+A4 = 7.
View SolutionThe equation of the plane containing the lines →r=a1+λ→band→r=→a2+μ→b is
View SolutionIf A1,A2 are between two numbers, then A1+A2H1+H2 is equal to
View SolutionThe resultant amplitude, when two waves of two waves of same frequency but with amplitudes a1 and a2 superimpose at phase difference of π/2 will be :-
View SolutionA1 and A2 are two vectors such that |A1|=3,|A2|=5 and |A1+A2|=5 the value of (2A1+3A2).(2A1−2A2) is
View Solution
