In a series circuit, at the frequencies and of source, the current amplitude falls to of the current amplitude at resonance. Then the value of is
The correct Answer is:A
(say at angular frequencies and )
solving ….(i)
....(ii)
Adding, .....(iii)
Substracting and using (iii)
Topper's Solved these Questions
- ALTERNATING CURRENTBook:NARAYNAChapter:ALTERNATING CURRENTExercise:LEVEL - VI
Explore 120 Videos
- ALTERNATING CURRENTBook:NARAYNAChapter:ALTERNATING CURRENTExercise:LEVEL - I (H.W)
Explore 23 Videos
- ALTERNATING CURRENTBook:NARAYNAChapter:ALTERNATING CURRENTExercise:LEVEL - IV NCERT Based Questions
Explore 15 Videos
- ATOMIC PHYSICSBook:NARAYNAChapter:ATOMIC PHYSICSExercise:LEVEL-II (H.W)
Explore 14 Videos
Similar Questions
In a series LCR circuit, the frequencies at which the current amplitude is1√2mes the current amplitude at resonance aref1andf2(>f1). Find the frequency bandwidth of resonance which is defined as Δf=f2−f1. Express your answer in terms of R and L. Assume that resonance frequency f0>>Δf
View SolutionA series LCR circuit is connected to a 45sin(ωt) Volt source. The resonant angular frequency of the circuit is 105rads−1 and current amplitude at resonance is l0. When the angular frequency of the source is ω=8×104rads−1 , the current amplitude in the circuit is 0.05I0. If L=50mH, match each entry in List-I with an appropriate value from List-II and choose the correct option.

View Solution
Knowledge Check
In a series LCR circuit, impedance Z is same at two frequencies f1 and f2. Therefore, the resonant frequency of this circuit is
Af1+f22B2f1f2f1+f2C√f21+f222D√f1f2In series LCR circuit, the phase angle between supply voltage and current is
AπradBπ2radC(pi)/(4)radDzero radAt resonant frequency the current amplitude in series LCR circuit is
AmaximumBminimumCzeroDinfinity
For the sereis LCR circuit shown in figure, the resonating frequency and current amplitude at resonance respectivley are

View SolutionFor the sereis LCR circuit shown in figure, the resonating frequency and current amplitude at resonance respectivley are

View SolutionIn a series LCR circuit, the frequency of the source is more than resonance frequency. The current in the circuit leads the voltage in phases(True/false).
View SolutionIn the given figure , a series L-C-R circuit is connected to a variable frequency source of 230 V . The impedance and amplitude of the current at the resonating frequency will be
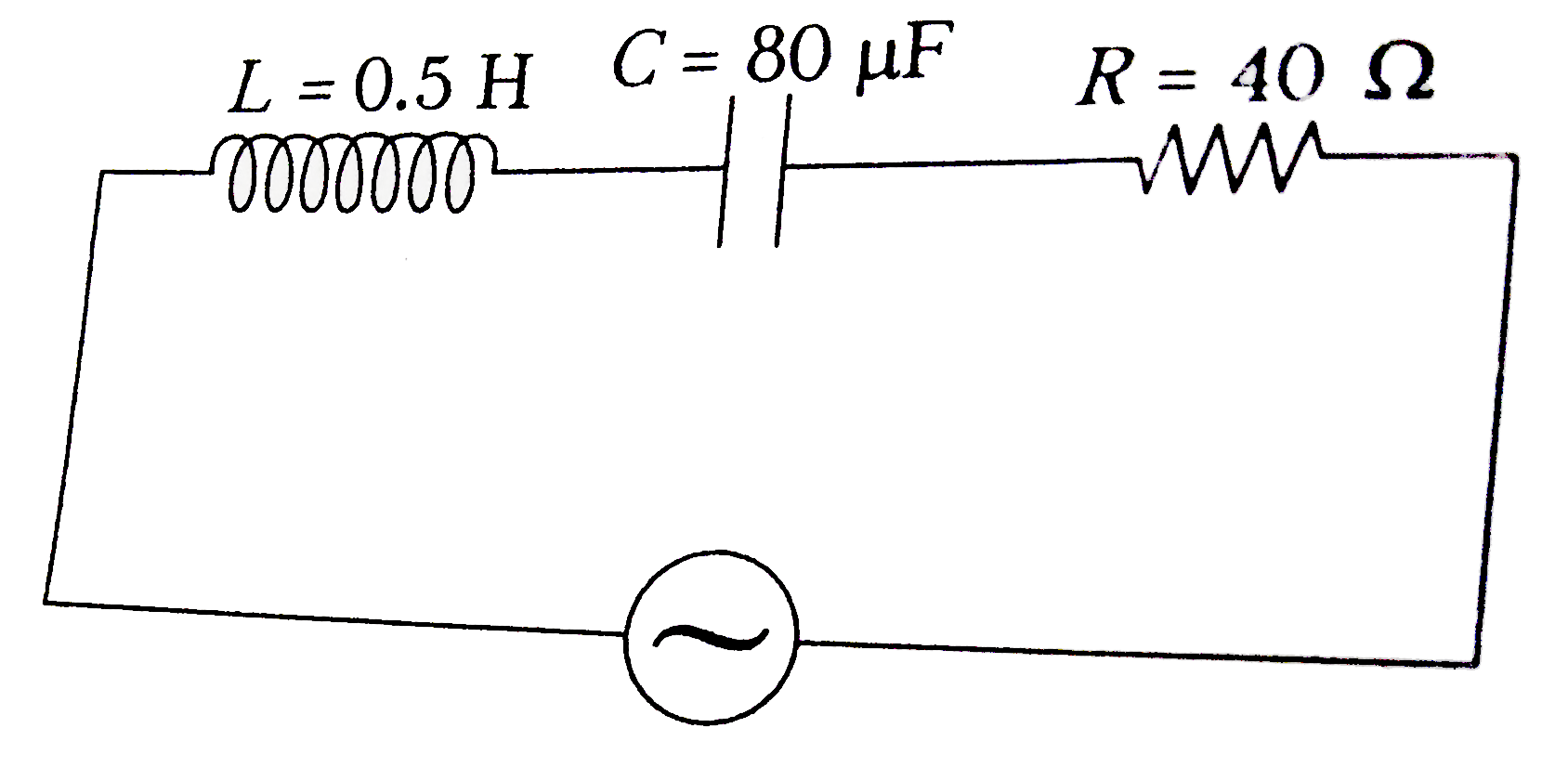
View SolutionFor the series LCR circuit shown in the figure, what is the resonance frequency and the amplitude of the current at the resonating frequency
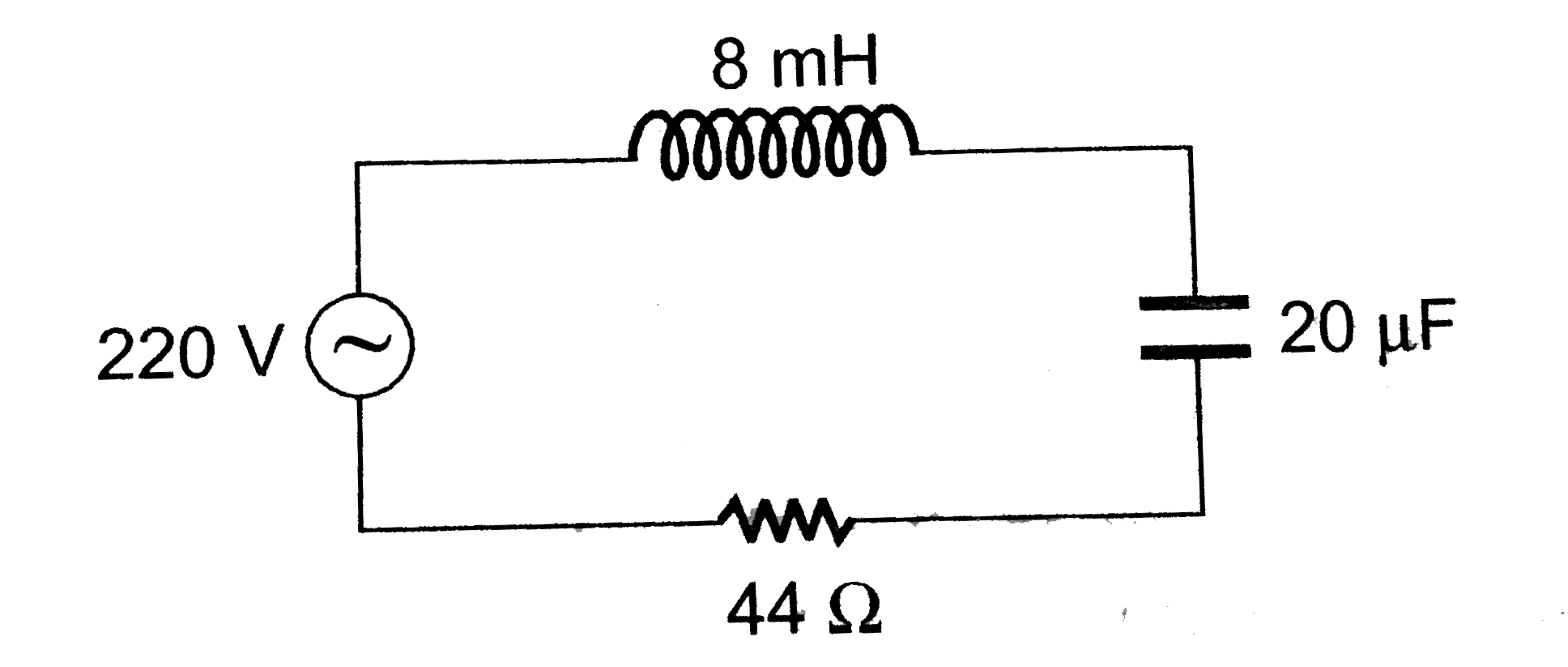
View Solution

