The average current of a sinusoidally varrying alternating current of peak value 5A with initial phase zero, between the instants t=T/8 to t=T/4 is (where 'T' is time period)
10π√2A
5π√2A
20√2π
10πA
The correct Answer is:1
To find the average current of a sinusoidally varying alternating current with a peak value of 5A and an initial phase of zero between the instants t=T8 and t=T4, we can follow these steps:
Step 1: Write the equation for the alternating current
The equation for the alternating current i(t) can be expressed as:
i(t)=I0sin(ωt)
where I0 is the peak current, and ω is the angular frequency.
Given that I0=5A and the initial phase is zero, we have:
i(t)=5sin(ωt)
Step 2: Determine the angular frequency ω
The angular frequency ω is related to the time period T by:
ω=2πT
Step 3: Set the limits for the average current calculation
We need to calculate the average current between t=T8 and t=T4.
Step 4: Use the formula for average current
The average current Iavg over a time interval from t1 to t2 is given by:
Iavg=1t2−t1∫t2t1i(t)dt
Substituting our limits:
Iavg=1T4−T8∫T4T85sin(ωt)dt
Step 5: Calculate the time interval
The time interval is:
T4−T8=2T8−T8=T8
Step 6: Substitute the time interval into the average current formula
Thus, we have:
Iavg=1T8∫T4T85sin(ωt)dt
=8∫T4T85sin(ωt)dt
Step 7: Evaluate the integral
The integral of 5sin(ωt) is:
∫5sin(ωt)dt=−5ωcos(ωt)
Now, we evaluate it from T8 to T4:
=−5ω(cos(ωT4)−cos(ωT8))
Step 8: Substitute ω=2πT
Substituting ω:
=−5T2π(cos(2πT⋅T4)−cos(2πT⋅T8))
=−5T2π(cos(π2)−cos(π4))
=−5T2π(0−1√2)
=5T2π√2
Step 9: Calculate the average current
Now substituting back into the average current formula:
Iavg=8⋅5T2π√2=40T2π√2=20Tπ√2
Final Result
The average current between t=T8 and t=T4 is:
Iavg=20π√2A
The equation for the alternating current i(t) can be expressed as:
i(t)=I0sin(ωt)
where I0 is the peak current, and ω is the angular frequency.
i(t)=5sin(ωt)
The angular frequency ω is related to the time period T by:
ω=2πT
We need to calculate the average current between t=T8 and t=T4.
The average current Iavg over a time interval from t1 to t2 is given by:
Iavg=1t2−t1∫t2t1i(t)dt
Substituting our limits:
Iavg=1T4−T8∫T4T85sin(ωt)dt
The time interval is:
T4−T8=2T8−T8=T8
Thus, we have:
Iavg=1T8∫T4T85sin(ωt)dt
=8∫T4T85sin(ωt)dt
The integral of 5sin(ωt) is:
∫5sin(ωt)dt=−5ωcos(ωt)
Now, we evaluate it from T8 to T4:
=−5ω(cos(ωT4)−cos(ωT8))
Substituting ω:
=−5T2π(cos(2πT⋅T4)−cos(2πT⋅T8))
=−5T2π(cos(π2)−cos(π4))
=−5T2π(0−1√2)
=5T2π√2
Now substituting back into the average current formula:
Iavg=8⋅5T2π√2=40T2π√2=20Tπ√2
The average current between t=T8 and t=T4 is:
Iavg=20π√2A
Topper's Solved these Questions
- ALTERNATING CURRENTBook:NARAYNAChapter:ALTERNATING CURRENTExercise:LEVEL - III (C.W)
Explore 24 Videos
- ALTERNATING CURRENTBook:NARAYNAChapter:ALTERNATING CURRENTExercise:NCERT Based Question
Explore 1 Video
- ALTERNATING CURRENTBook:NARAYNAChapter:ALTERNATING CURRENTExercise:LEVEL - I (C.W)
Explore 23 Videos
- ATOMIC PHYSICSBook:NARAYNAChapter:ATOMIC PHYSICSExercise:LEVEL-II (H.W)
Explore 14 Videos
Similar Questions
An alternating current I=I0sinωt is flowing in a circuit.The ratio of rms current in the interval of 0 to T the average current in the circuit for the time interval from T/8 to 3T/8 (Where T is time period) is :
View SolutionAn alternating current I=I_(0)sin omega t is flowing in a circuit.The ratio of rms current in the interval of 0 to T the average current in the circuit for the time interval from T/8 to 3T/8 (Where T is time period) is:
View Solution
Knowledge Check
The average value of current for the current shown for time period 0 to T2 s
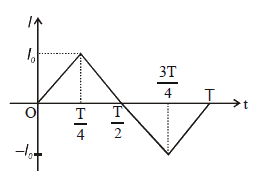 Al0√2Bl02Cl0√3Dl02√3
Al0√2Bl02Cl0√3Dl02√3The period of SHM of a particle is 12 s. The phase difference between the positions at t = 3 s and t = 4 s will be
Aπ/4B3π/5Cπ/6Dπ/2The alternating current in a circuit is given by I=50sin314t. The peak value and frequency of the current are
AI0=25 A and f=100HzBI0=50 A and f=50 HzCI0 = 50 A and f=100 HzDI0=25 A and f=50 Hz
An alternating current I=I_(0) sin omega t is flowing in a circuit.The ratio of rms current in the interval of 0 to T the average current in the circuit for the time interval from T/8 to 3T/8 (Where T is time period) is :
View SolutionWhat is the average value of atlernating current, I=I0sinωt over time interval t=π/ω to t=π/ω ?
View SolutionAn alternating current I=I0sinwt is flowing in a circuit. The ratio of rms current in the interval of 0 to T to the average current in the circuit for the time interval from T/8 to 3T/8 (Where T is time period) is :
View SolutionThe electric current in a circuit is given by i = 3t. Find the rms current for the period t = 0 to t = 2 sec
View SolutionAn alternating current is given by the equation i=i_(1)sin ω t+i_(2)cosω t .The rms current will be :
View Solution

