A long straight wire carries an electric current of 2A. The magnetic induction at a perpendicular distance of 5m from the wire is (μ04π×107Hm−1)
4×10−8T
8×10−8T
12×10−8T
16×10−8T
The correct Answer is:2
To find the magnetic induction (B) at a perpendicular distance from a long straight wire carrying an electric current, we can use the formula:
B=μ0I2πD
Where:
- B is the magnetic induction,
- μ0 is the permeability of free space, given as 4π×10−7H/m,
- I is the current in amperes,
- D is the perpendicular distance from the wire in meters.
1. Identify the given values:
- Current, I=2A
- Distance, D=5m
- Permeability of free space, μ0=4π×10−7H/m
2. Substitute the values into the formula:
B=4π×10−7×22π×5
3. Simplify the expression:
- The 2π in the numerator and denominator cancels out:
B=4×10−7×210=8×10−710
4. Calculate the final value:
B=8×10−8T
Thus, the magnetic induction at a perpendicular distance of 5 m from the wire is 8×10−8T.
- B is the magnetic induction,
- μ0 is the permeability of free space, given as 4π×10−7H/m,
- I is the current in amperes,
- D is the perpendicular distance from the wire in meters.
- Current, I=2A
- Distance, D=5m
- Permeability of free space, μ0=4π×10−7H/m
B=4π×10−7×22π×5
- The 2π in the numerator and denominator cancels out:
B=4×10−7×210=8×10−710
B=8×10−8T
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:Level -II (H.W)
Explore 37 Videos
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:ILLUSTRATION
Explore 58 Videos
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:LEVEL-VI (SINGLE ANSWER QUESTION)
Explore 81 Videos
- MAGNETISM AND MATTERBook:NARAYNAChapter:MAGNETISM AND MATTERExercise:EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
Explore 17 Videos
- NUCLEAR PHYSICSBook:NARAYNAChapter:NUCLEAR PHYSICSExercise:LEVEL-II-(H.W)
Explore 9 Videos
Similar Questions
A long straight wire carries a current of 35A. What is the magnetic of the field →B at a point 20cm from the wire?
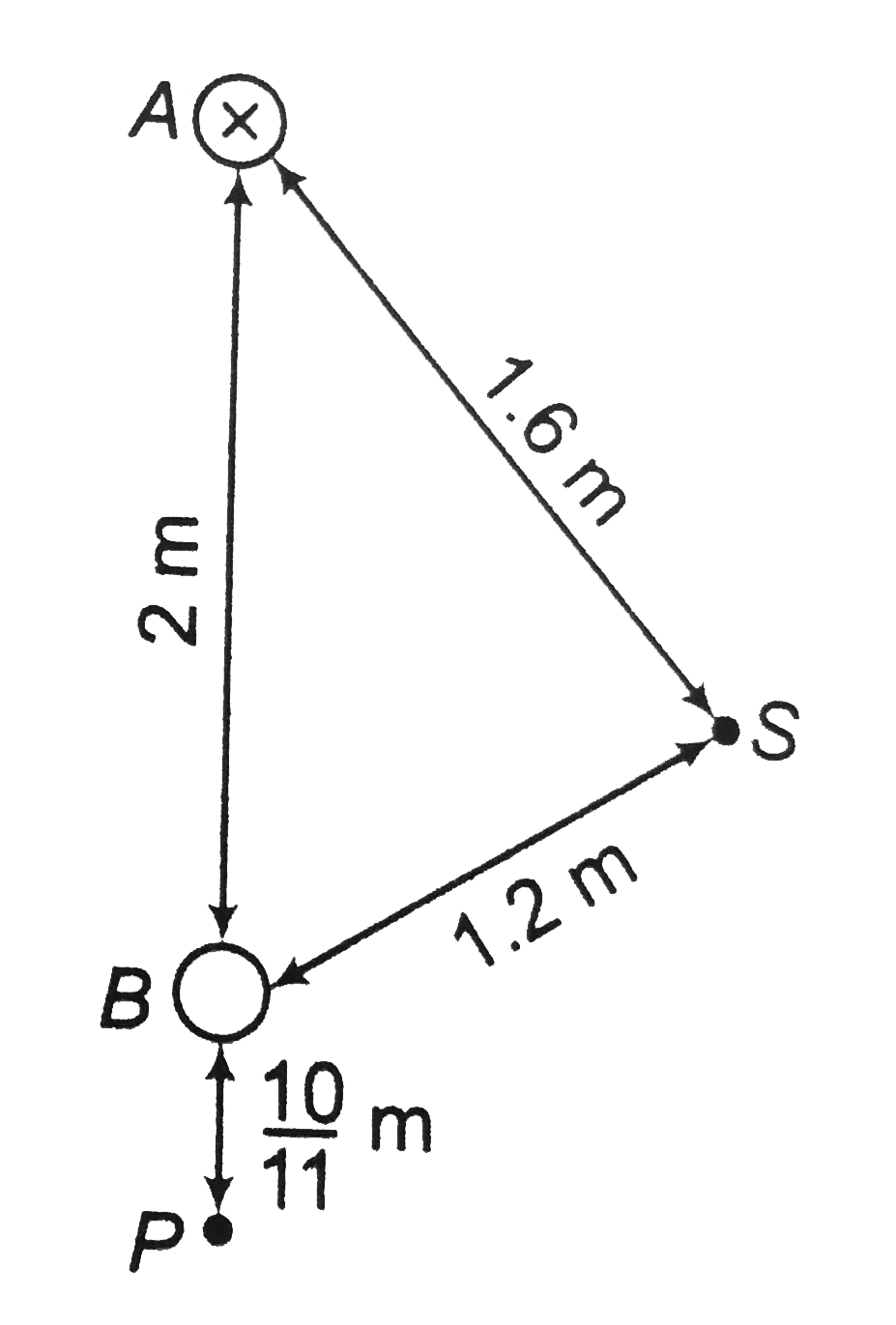
View SolutionTwo long straight parallel wieres are 2m apart, perpendicular to the plane of the paper. The wire A carries a current of 9.6A, directed into the plane of the paper. The wire B carries a current such that the magnetic field of induction at the point P, at a distance of 1011 m from the wire B, is zero. find
a. the magnitude and directiion of the current in B.
b. the magnitude of the magnetic field of induction of the pont S.
c. the force per unit length on the wire B.
View Solution
Knowledge Check
A long straight cable contains 7 strands of wire each carrying a current of 5 A. The magnetic induction at a distance of 2 cm from the axis of the cable is
A5×10−5 TB3.5×10−4 TC3.5×10−4 TD1.1×10−3 TA long straight wire is carrying a current of 12 A . The magnetic field at a distance of 8 cm is
(μ0=4π×10−7NA2)A2×10−4wb/m2B3×10−5Wb/m2C4×10−4Wb/m2D4×10−5Wb/m2What is the magnetic induction at a distance of 5 cm from a straight wire carrying a current of 5 mA ?
A4×10−8Wb/m2B3×10−8Wb/m2C2×10−8Wb/m2D5.5×10−8Wb/m2
A long straight wire carries a current of πamp. The magnetic field due to it will be 5×10−5weber/m2 at what distance from the wire [μ0= permeability of air]
View SolutionA long straight wire carrying a current of 30 A is placed in an external unifom magnetic field of intensity 4×10−4 T. The magnetic field is acting parallel to the direction of current. The magnitude of the resultant magnetic induction in tesla at a point 2.0 cm away from the wire is (μ0=4π×10−7Hm−1)
View SolutionA very long straight wire of radius 'r carries current 'I'. Intensity of magnetic field 'B' at a point, lying at a perpendicular distance 'a' from the axis is ∝ ___________
View SolutionThe magnetic induction at any point due to a long straight wire carrying a current is
View SolutionA long straight wire carries a current of 10 A. An electron travels perpendicular to the plane of this wire at a distance 0.1 m with a velocity of 5.0×106m/s. What is the force acting on the electron due to the current in wire ?
View Solution

