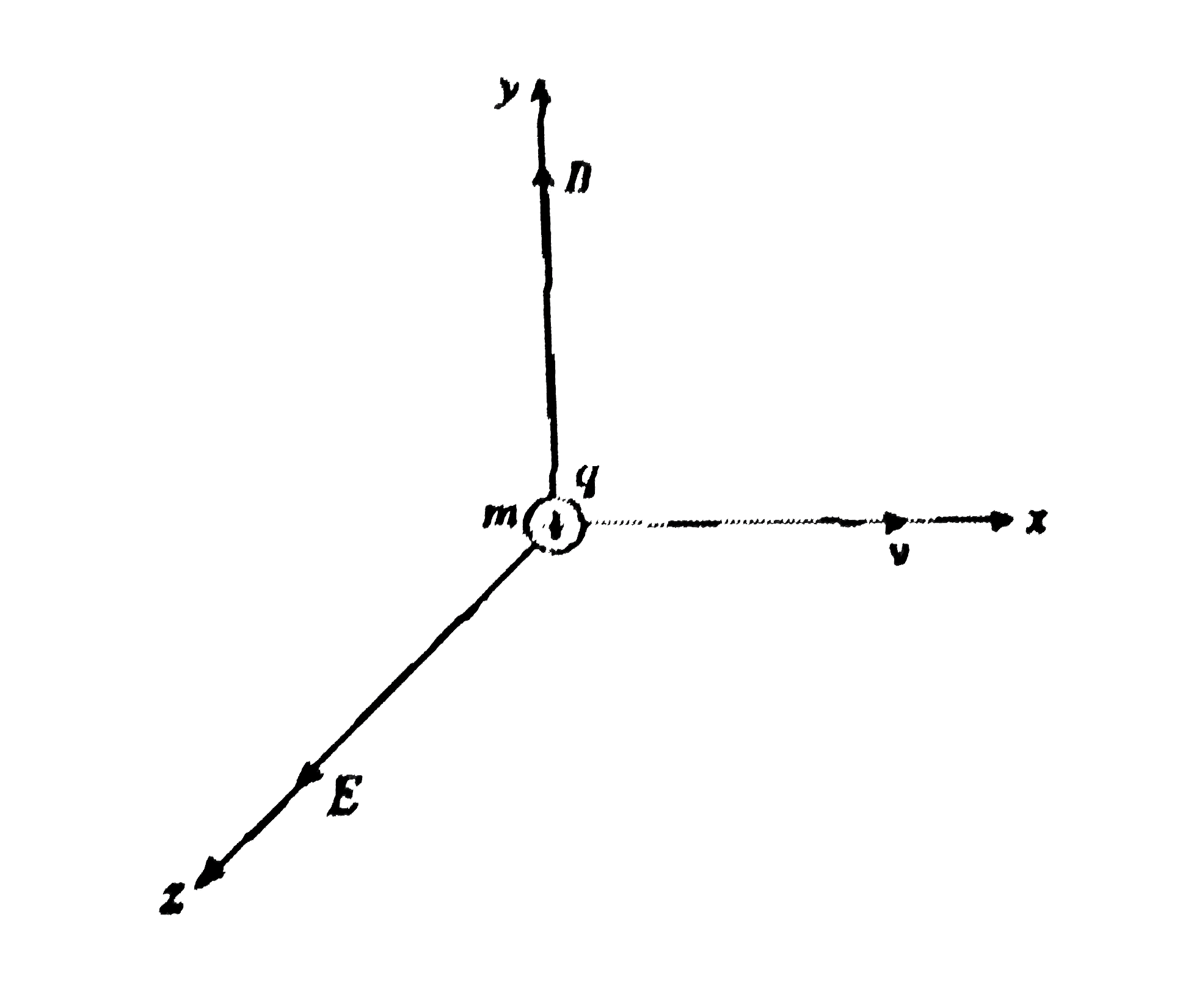
A charged particle of mass m and charge q is projected on a rough horizontal XY plane. Both electric and magnetic fields are given by →E=−10ˆkN/C and magnetic field →B=−5→k tesla are present in the region. The particle enters into the magnetic field at (4,0,0)m with a velocity 50→jm/sec. The particle starts into a curved path on the plane. If coefficietn of friction μ=13 between particle and plane, then (qE=2mg,g=10m/s2).
Radius of curvature of the path followed by particle, initially is
5m
2.5m
1.25m
10m
The correct Answer is:A
r=mvqB=m×50q×5=m×102mg×10=5m
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Level =I (H.W)
42 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Level -II (H.W)
37 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - LEVEL-V (SINGLE ANSWER QUESTION)
85 Videos
- MAGNETISM AND MATTERBOOK - NARAYNACHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
17 Videos
- NUCLEAR PHYSICSBOOK - NARAYNACHAPTER - NUCLEAR PHYSICSEXERCISE - LEVEL-II-(H.W)
9 Videos
Similar Questions
A charged particle of mass m and charge q is projected on a rough horizontally xy− plane surface with z− axis in the vertically upward direction. Both electric and magnetic fields are acting in the region and given by →E=−E0ˆk and →B=−B0ˆk respectively. The particle enters into the field at (a,0,0) with velocity →v=υ0ˆj. The particle starts moving into a circular path on the plane. If the coefficient of friction between the particle and the plane is μ. Then calculate tha :

(a) time when the particle will come to rest
(b) time when the particle will hit the centre.
(c) distance travelled by the particle when it comes to rest.
View SolutionA positively charged particle of mass m and charge q is projected on a rough horizontal x-y plane surface with z-axis in the vertically upward direction. Both electric and magnetic fields are acting in the region and given by →E=−E0ˆkand→B=−B0ˆk , respectively. The particle enters into the field at (a0,0,0) with velocity →v=v0ˆj. The particle starts moving in some curved path on the plane. If the coefficient of friction between the particle and the plane is μ. Then calculate the
(a) time when the particle will come to rest
(b) distance travelled by the particle when it comes to rest.

View Solution
Knowledge Check
A charged particle of mass m and charge q is projected on a rough horizontal XY plane. Both electric and magnetic fields are given by →E=−10ˆkN/C and magnetic field →B=−5→k tesla are present in the region. The particle enters into the magnetic field at (4,0,0)m with a velocity 50→jm/sec. The particle starts into a curved path on the plane. If coefficietn of friction μ=13 between particle and plane, then (qE=2mg,g=10m/s2).
Total distance covered by the particle isA100mB125mC200mD50mA charged particle of mass m and charge q is projected on a rough horizontal XY plane. Both electric and magnetic fields are given by →E=−10ˆkN/C and magnetic field →B=−5→k tesla are present in the region. The particle enters into the magnetic field at (4,0,0)m with a velocity 50→jm/sec. The particle starts into a curved path on the plane. If coefficietn of friction μ=13 between particle and plane, then (qE=2mg,g=10m/s2).
Total work done by electric force on the particle isA250JBzeroC125JDnoneA charged particle of mass m and charge q is projected on a rough horizontal XY plane. Both electric and magnetic fields are given by →E=−10ˆkN/C and magnetic field →B=−5→k tesla are present in the region. The particle enters into the magnetic field at (4,0,0)m with a velocity 50→jm/sec. The particle starts into a curved path on the plane. If coefficietn of friction μ=13 between particle and plane, then (qE=2mg,g=10m/s2).
The time after which particle comes to rest, isA5sB4sC3sD1s
A particle having mass m and charge q is released from the origin in a region in which electric field and megnetic field are given by →B=−B0ˆj and →E=→E0ˆk. Find the speed of the particle as a function of its z-coordinate.
View SolutionA charge particle of charge q, mass m is projected with a velocity →v=vˆi in a region of space where electric field strength →E=Eˆk and magnetic induction →B=Bˆj are present. The acceleration of the particle is:
View SolutionA particle of mass m and charge q is thrown in a region where uniform gravitational field and electric field are present. The path of particle:
View SolutionA charged particle enters into a magnetic field with velocity vector making an angle of 30∘ with respect of the direction of magnetic field. The path of the particle is
View SolutionA particle of mass m and charge q is in an electric and magnetic field given by →E=2i+3ˆj,→B=4ˆj+6k.The charged particle is shifted from the origin to the point P(x=1,Y=1) along a straight path. The magnitude of the total work done is:
View Solution
